日常生活でひんぱんに利用されるがいねんが割合です。割合を利用することによって、どれだけの量があるのか把握できるようになります。
小学算数の中でも、割合の計算はむずかしいです。割合の計算をするとき、わり算を利用します。ただ、どの数を利用してわり算をすればいいのか理解しにくいのです。そのため公式を利用するのではなく、計算方法や考え方を理解しなければいけません。
また割合を理解すれば、百分率(パーセント)や歩合を学ぶことができます。百分率や歩合は多くの場面で利用されています。
買い物や旅行など、さまざまな場面で割合を利用します。そこで、どのように割合の計算をすればいいのか解説していきます。
もくじ
割合とは何か:何倍になるのかを知る
まず、割合とは何なのでしょうか。割合では、「基準となる数に対していくらの量があるのか」を表します。
例えば、2を何倍すると10になるでしょうか。2を5倍すれば10になります。このとき、5倍が割合です。また、2を何倍すれば0.2になるでしょうか。2を0.1倍すれば0.2になります。このとき、0.1倍が割合です。
つまり基準となる数に対して、何倍すれば得たい答えを得られるのかを考えます。先ほどの例であれば、2(基準となる数)に何の数をかけると10や0.2になるのか考えました。このとき、かける数が割合です。
このように、何倍にすればいいのかを知るために割合を利用します。割合は日常生活でひんぱんに利用されます。例えば旅行をするとき、100kmを移動するのと120kmを移動するのでは、どれだけの違いがあるでしょうか。この違いを表すのが割合です。
値段や距離、重さを比較するとき、割合が利用されます。割合を使うことによって、どれくらいの違いがあるのかわかるようになるのです。
「基準となる数」と「合計の数」を利用して計算する割合の公式
それでは、どのように割合を計算すればいいのでしょうか。これについては、基準となる数と合計の数を見つけましょう。
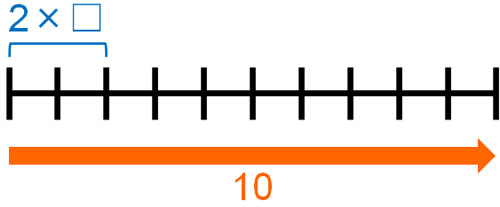
先ほど、2を5倍すれば10になると解説しました。これは、2を基準となる数とするとき、何倍すれば10(合計の数)になるのかを意味しています。
 覚えるようにしましょう。公式
覚えるようにしましょう。公式
\(☐\)に入る数字が割合です。基準となる数と合計の量がわかれば、割合を計算することができます。そこで\(☐\)を利用し、式を作りましょう。以下のようになります。
- 基準となる数 × \(☐\) = 合計の数
割合の計算する場合、すべてこの式を利用するようにしましょう。
\(☐\)を利用して割合を求める式を作る
それでは、実際に割合の問題を解いてみましょう。例えば、以下の問題の答えは何でしょうか。
- 12mの\(☐\)倍は7.2mです
- 15gは\(☐\)gの3倍です
・(1)の解答
何倍すればいいのかを表すのが割合であるため、割合は\(☐\)です。一方で12mと7.2mのうち、基準となる数はどちらでしょうか。
12mを\(☐\)倍すると、7.2mになります。つまり、「12mを基準として\(☐\)倍すると、7.2mになる」と言い換えることができます。そのため、基準となる数は12mです。12mを\(☐\)倍した結果、合計で7.2mになるため、以下の計算式を作ることができます。
\(12×☐=7.2\)
この式を解くと、以下のようになります。
\(12×☐=7.2\)
\(☐=7.2÷12\)
\(☐=0.6\)
こうして、割合(\(☐\))は0.6であるとわかります。
・(2)の解答
「15gは\(☐\)gの3倍」では、割合は3とすでにわかっています。それでは、基準となる数は15gと\(☐\)gのうち、どちらでしょうか。この文章を確認すると、「\(☐\)gを3倍すると15gになる」と言い換えることができます。つまり、基準となる数は\(☐\)gです。そこで、以下の式を作りましょう。
- \(☐×3=15\)
これを解くと、以下のようになります。
\(☐×3=15\)
\(☐=15÷3\)
\(☐=5\)
こうして、5gが答えになります。
割合の公式を覚えてはいけない
なお小学算数で割合を学ぶとき、教科書には公式が記載されています。具体的には、以下の公式になります。
- 割合 = 比べられる量 ÷ もとにする量
- 比べられる量 = もとにする量 × 割合
- もとにする量 = 比べられる量 ÷ 割合
ただ、この公式は絶対に覚えないようにしましょう。覚えてもいいですが、ほとんどの人で利用することができないからです。
まず、日常生活で「もとにする数」「比べられる数」という言葉を利用することはありません。そのため、計算するときにイメージしにくいです。そのため、必ず「基準となる数」「全体の量」という言葉と以下の式を利用しましょう。
- 基準となる数 × \(☐\) = 合計の数
※参考までに、アメリカやヨーロッパでは割合の計算をするとき、基準(Base)と量(Amount)を公式として利用します。また、これを利用するほうが圧倒的にわかりやすいです。
また教科書に記載された公式3つを覚える必要はありません。先に示した一つの公式(基準となる数 × \(☐\) = 合計の数)のみ覚えるようにしましょう。公式を3つ覚えても、どの公式を利用すればいいのかわかりません。そこで、一つの公式のみ利用しましょう。
百分率(パーセント)を理解する
割合について理解すれば、百分率(パーセント)を学ぶことができます。割合とパーセントは似ています。ただ、数字の表現方法が異なります。
割合では、2や0.1、5などの数字を利用して表します。基準となる数に対して、何倍すれば合計の数になるのかを表すのが割合です。百分率についても同様であり、基準となる数に対して何倍すれば合計の数になるのか表すのが百分率です。
ただ割合と百分率では表現方法が異なります。割合と百分率を比べると以下のようになります。
| 割合 | 百分率 |
| 1 | 100% |
| 1.2 | 120% |
| 0.5 | 50% |
| 0.01 | 1% |
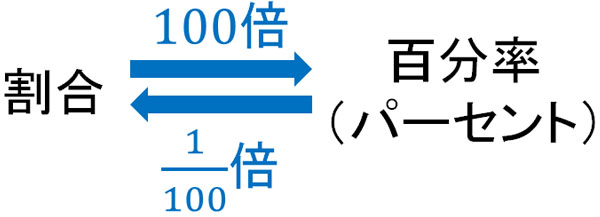
このように、割合の数字に対して100倍した後、%を加えることで百分率になります。割合の数字を100倍すれば百分率になり、百分率の数字を100でわると割合になります。百分率では「1=100%」と考えるのです。
小さい変化を表すとき、一般的に百分率を利用することが多いです。例えば水の量が減るとき、「水の量が0.85倍に減る」よりも、「水の量が85%に減る」と表現するほうがわかりやすいです。
一方で大きな変化を表すとき、割合を利用するほうが理解しやすいです。例えば「お金が1200%に増える」よりも、「お金が12倍に増える」と表現するほうがわかりやすいです。割合と百分率は両方利用されるものの、使われる場面が異なります。
それでは、実際の問題を解いてみましょう。以下の答えは何でしょうか。
- 1400gの\(☐\)%は980gです
割合は\(☐\)です。それでは、基準となる数と全体の量は何でしょうか。先ほどの問題文について、「1400gを基準に\(☐\)倍すると980gになる」と言い換えることができます。そのため基準となる数は1400gであり、以下の式を作ることができます。
- \(1400×☐=980\)
この式を解くと以下のようになります。
\(1400×☐=980\)
\(☐=980÷1400\)
\(☐=0.7\)
こうして、割合は0.7であるとわかります。ただ問題文を見ると、答えを百分率でださなければいけません。そこで0.7に100をかけて、パーセントで答えをだしましょう。つまり、答えは70%です。
百分率を変化させたのが歩合
パーセントを学べば、歩合を理解するのは簡単です。百分率で表す数字について、以下の部分をそれぞれ「割・分・厘」といいます。

例えば0.123では、1割2分3厘と表現します。0.425では4割2分5厘と表現します。そのため歩合を利用する場合、以下のように、小数点の位置によって呼び方が変わると理解しましょう。
- 0.1の部分:割
- 0.01の部分:分
- 0.001の部分:厘
それでは、80gの3割は何gでしょうか。3割の割合は0.3です(百分率では30%)。そのため80gに0.3をかけると以下のようになります。
- \(80×0.3=24\)
そのため、80gの3割は24gです。
割増しと割引の計算方法
割合や百分率、歩合を理解した後、応用問題を解いてみましょう。日常生活では、旅行のときに金額の割増しがあったり、買い物のときに割引があったりします。割合を学べば、割増しや割引の計算も可能になります。
・割増しの計算
例えば、以下の問題の答えは何でしょうか。
- 20000円で宿泊できるホテルに泊まります。ただ、7割増しでお金を払うと、スイートルーム(高級な部屋)に宿泊できます。スイートルームの宿泊料金はいくらですか。
7割を割合に変えると0.7(70%)です。そのため、\(20000×0.7=14000\)円を追加で支払えば、スイートルームに宿泊できます。そのため、スイートルームの宿泊料金は以下になります。
- \(20000+14000=34000\)円
割増料金を計算するとき、元の値段と割増料金をたすようにしましょう。
・割引の計算
一方で割引はどのように計算すればいいのでしょうか。以下の問題を計算してみましょう。
- 20000円で宿泊できるホテルに泊まります。ただ朝食なしにすると、1割引きで宿泊できます。朝食なしの宿泊料金はいくらですか。
1割を割合に変えると0.1(10%)です。つまり朝食なしにすると、\(20000×0.1=2000\)円の割引があります。そのため、朝食なしでの宿泊料金は以下になります。
- \(20000-2000=18000\)円
割引料金を計算するとき、元の金額から割引金額をひくようにしましょう。
割合・百分率・歩合の計算を行う
私たちは多くの場面で割合や百分率、歩合を利用します。割合が多くの場面で利用されるのは便利だからです。割合や百分率、歩合で数字を表現することによって、何倍の量になるのか把握することができるのです。
割合を理解していない場合、買い物や旅行など多くの場面で困ることになります。そのため、計算方法を理解しましょう。
割合の計算では、必ず基準となる数と全体の数を利用しましょう。教科書に載っている公式は忘れていいです。また百分率の計算では、割合の数字に対して100をかける必要があることを理解しましょう。
割合の計算で最も重要なのは、どの数が基準となる数なのかを見分けることです。これができれば、割合の計算は難しくありません。