小学算数ではかけ算を習います。わたしたちの日常生活でかけ算はひんぱんに利用されます。たとえばかけ算をすることができなければ、買い物でお金の計算をすることができません。そのため、かけ算ができるようになる必要があります。
それでは、どのようにかけ算をすればいいのでしょうか。まずは、かけ算の意味を理解しなければいけません。
また整数について1ケタのかけ算だけでなく、2ケタや3ケタのかけ算をできるようにしましょう。そこでケタの少ないかけ算だけでなく、ケタの多いかけ算についても、どのように筆算をすればいいのかについて解説していきます。
もくじ
かけ算の計算が必要な理由
なぜ、かけ算をする必要があるのでしょうか。それは、かけ算をするほうが計算が速いからです。たとえば、以下の問題の答えは何でしょうか。
- 一台に4人が乗れる車があります。この車が5つあれば何人乗れますか?
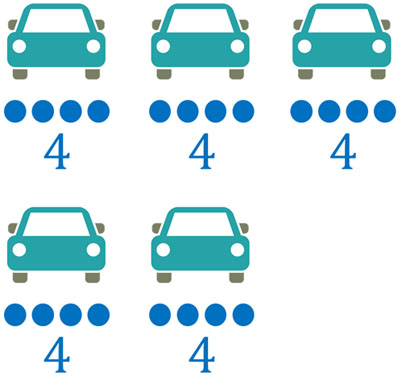
一つの車に4人が乗れるため、たし算によって以下のように計算できます。
- \(4+4+4+4+4=20\)
ただ、このやり方では計算スピードが遅いです。そこで、かけ算を使いましょう。かけ算であれば、以下のようにすぐに計算できます。
- \(4×5=20\)
4人乗れる車が5つあるため、\(4×5\)という式をつくることができます。
それではつぎに、4人が乗れる車について、車の数を一つずつ増やしていきましょう。車に乗れる人数は以下のようになります。
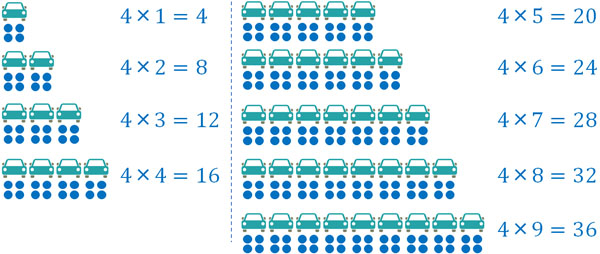
このように車が一つ増えると、乗れる人数は4人ずつ増えます。かけ算を使えば、車に乗れる人数をすぐに計算することができます。
すべての九九を覚えるべき
そこで、1ケタのかけ算をすべて覚えてしましょう。覚えなければ、算数の計算をすることができません。数字のかけ算をするとき、1ケタのかけ算で何が答えになるのかすぐに解答できるようにするのです。
1ケタと1ケタのかけ算について、以下の九九の表を覚える必要があります。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
この九九の表より、以下のように計算できます。
- \(2×7=14\)
- \(6×3=18\)
- \(4×9=36\)

もちろん、すべてのかけ算を覚えるのは難しいです。そこで二の段や五の段など、かんたんなかけ算から覚えるようにしましょう。
また、おとなであったとしても七の段や八の段は難しく、計算を間違えることは何度もあります。そこで、くり返し勉強することで1ケタのかけ算をすべて覚えるようにしましょう。
かけ算の筆算をする:1ケタと2ケタ
1ケタと1ケタのかけ算ができるようになったあと、つぎは1ケタと2ケタのかけ算を学びましょう。筆算をすることによって、1ケタと2ケタのかけ算をすることができます。たとえば、以下の計算はどのようにすればいいでしょうか。
- \(34×6\)
この計算をするとき、以下の式をつくりましょう。
\(\begin{array}{rr}
& 34\\
×\big{)}&6\\
\hline
\end{array}\)
おとなであっても、1ケタと2ケタの計算を暗算でするのは難しいです。そこで、1ケタどうしのかけ算でない場合、かならずこの式をつくりましょう。
やり方としては、まず1ケタのかけ算をしましょう。\(4×6\)をさきに計算します。
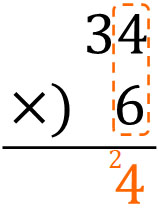
計算すると、\(4×6=24\)です。24のうち、4は一の位なのでそのまま書きます。いっぽう、2は十の位なのでくり上げなければいけません。そこで、数字を小さく書きましょう。十の位はまだ計算していないからです。
つぎに、十の位のかけ算をしましょう。\(3×6\)をして、十の位の計算をします。
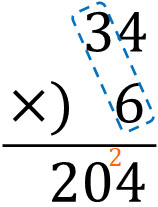
計算すると、\(3×6=18\)です。そこで、18を十の位に書きます。ただ一の位を計算したとき、2がくり上がっています。そこで、18に2を足します。\(18+2=20\)なので、十の位は18ではなく、20を書くようにしましょう。
こうして、答えが204とわかります。
2ケタのかけ算を計算する:2ケタと2ケタ
つぎに2ケタのかけ算をしましょう。1ケタと2ケタのかけ算にくらべると、計算がすこし複雑になります。たとえば、以下の計算はどのようにすればいいでしょうか。
- \(27×32\)
まずは、以下の式をつくりましょう。
\(\begin{array}{rr}
& 27\\
×\big{)}&32\\
\hline
\end{array}\)
最初にやるべき計算はさきほどと同じく、1ケタと2ケタの計算です。以下のようになります。
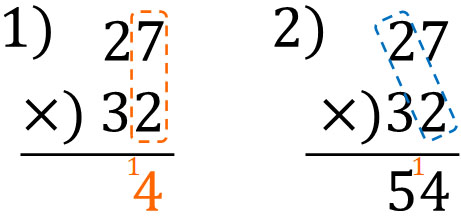
つぎに、\(27×3\)の計算をしましょう。重要なのは、3は十の位であることです。そのため、筆算をするときは一つ左にずらしましょう。以下のようになります。
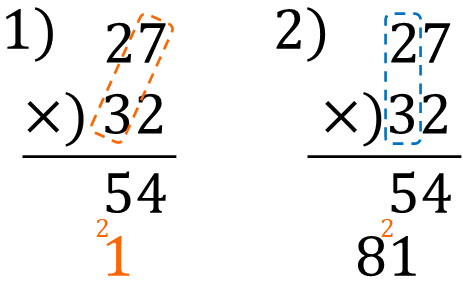
さいごに、計算した数字をたします。上下の数字をたすと、以下のようになります。
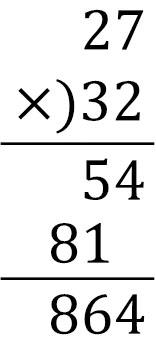
ポイントとしては、\(27×3\)の計算をするとき、一つ左にずらして書くことです。\(27×3\)の計算ではあっても、3は十の位なので、実際の計算は\(27×30\)です。そのため計算をするとき、一つ左にずらさなければいけません。
そのあと、上下の位に気をつけてたし算をしましょう。
3ケタのかけ算のやり方:2ケタと3ケタ
2ケタのかけ算ができるようになれば、3ケタのかけ算をすることもできます。やり方はさきほどと同じです。ただ3ケタになるため、くり上がりの計算に注意しましょう。たとえば、以下の計算はどうすればいいのでしょうか。
- \(463×34\)
まずは、以下の式をつくりましょう。
\(\begin{array}{rr}
& 463\\
×\big{)}&34\\
\hline
\end{array}\)
さきほどと同じように、まずは\(463×4\)を計算しましょう。
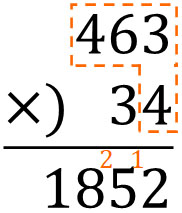
つぎに、\(463×3\)を計算します。3は十の位なので、一つ左にずらして書きます。
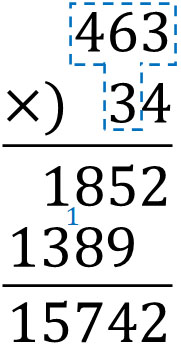
さいご、上下の数字をたすことで、答えは15742になります。
ゼロが多い数字の計算方法
なおかけ算をするとき、計算ミスしやすいのが0です。ゼロがたくさんあるとき、ケタを間違えてしまうのです。たとえば、以下の計算はどのようにすればいいでしょうか。
- \(260×200\)
筆算によって計算するとき、以下のようになります。
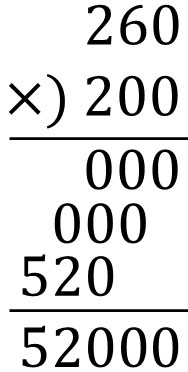
このように、答えは52000です。ただ、ゼロが多いので計算ミスしやすいです。そこで、より簡単な計算をしましょう。
ゼロがいくつもあるとき、ゼロ以外を計算しましょう。さきほどの計算であれば、\(260×200\)ではなく、\(26×2\)をさきに計算します。そのあと、省いた三つのゼロをくわえます。
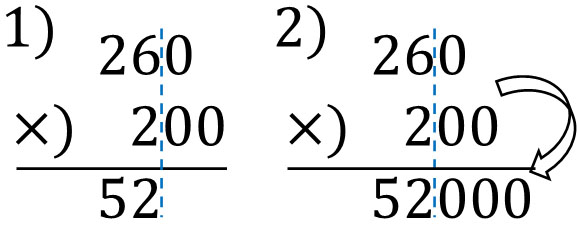
この計算によって、さきほどと同じ答え52000がでます。ゼロがあるとき、ゼロを省いて計算するとミスを防げます。そのあと、省いた数だけゼロをくわえると答えをだせます。
小学算数で学ぶかけ算の計算
たし算と引き算ができるようになったあと、つぎに学ぶのはかけ算です。そこで、かけ算ができるようにしましょう。
たし算や引き算とはちがい、かけ算では九九を覚えなければいけません。覚えなければかけ算の計算をすることはできません。そのため、なんども勉強することによって九九をいえるようにしましょう。
そのあと、2ケタや3ケタのかけ算ができるようになるといいです。筆算を使うことによって、ケタの多いかけ算であっても計算できるようになります。