小学校では算数で小数を学びます。小数ではかけ算の問題がひんぱんにでてくるため、かけ算ができるようになっていなければいけません。
小数のかけ算とはいっても、通常の筆算とやり方は同じです。小数点の位置に気を付ける必要はありますが、小数点があること以外は大きな違いはありません。
それでは、どのように小数のかけ算をすればいいのでしょうか。ここでは、小学算数で習う小数のかけ算のやり方を解説していきます。
もくじ
小数と整数のかけ算のやり方
まず、小数と整数のかけ算のやり方を学びましょう。どのように小数と整数のかけ算をすればいいのでしょうか。かけ算の筆算をするとき、数字を右にそろえましょう。たとえば、以下の計算問題があるとします。
- \(2.13×41\)
かけ算をするとき、以下の式を作りましょう。

そのあと、筆算をします。まずは小数点を無視して、かけ算をしましょう。そうして答えをだしたあと、小数点をそのまま下におろします。以下のようになります。
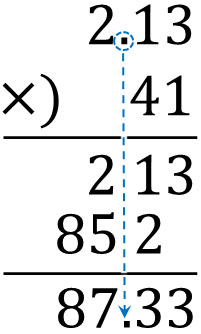
このステップによって、小数と整数のかけ算をすることができます。整数のかけ算と異なるのは、「答えをだしたあとに小数点を下におろすかどうか」だけです。
なぜ筆算で数字を右にそろえるのか
たし算や引き算では、必ずケタ数を合わせます。一方で小数のかけ算では、右にそろえます。なぜ、かけ算ではケタを合わせる必要がないのでしょうか。
すべてのかけ算に共通しますが、計算をするときにケタを合わせる必要はありません。特定の数字にたいして、何倍になっているのかを示すのがかけ算だからです。たとえば\(4.1×2\)というのは、4.1が2つあることを意味します。そのためケタを合わせるのではなく、数字を右にそろえます。
それに対して、たし算(または引き算)ではどうでしょうか。たとえば\(48-3\)を計算するとき、かならず一の位どうしで引き算をしなければいけません。48から3を引くとき、一の位である8から3を引かなければならず、十の位である4から3を引いてはいけません。たし算と引き算では、ケタが大きな意味をもつのです。
こうした理由があるため、たし算や引き算の筆算ではケタを合わせるものの、かけ算の筆算では右にそろえるようにします。
小数と小数のかけ算:小数点の位置に気を付ける
それでは、小数と小数のかけ算はどのようにすればいいでしょうか。小数と整数だけでなく、小数どうしのかけ算のやり方を理解しましょう。
基本的な考え方は同じです。かけ算の筆算をするとき、数字を右にそろえるようにしましょう。たとえば、以下の計算はどのようにすればいいでしょうか。
- \(3.24×1.2\)
まずは、以下のように筆算の式を作りましょう。
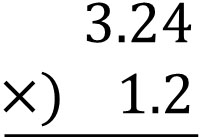
計算方法はさきほどと同じように、小数点を無視してかけ算をします。以下のようになります。
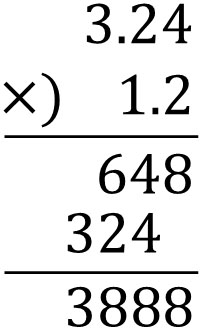
次に、無視をした小数点を答えに加えましょう。やり方としては、小数点を右にいくつ移動させることができるかを数えます。たとえば3.24であれば、小数点を右に2つ移動させることができます。また1.2であれば、小数点を右に1つ移動させることができます。
合計で小数点を3つ右に移動させることができるため、答えでは右から三番目の部分に小数点をつけます。以下のようになります。

このように、小数点を右へいくつ移動させることができるのかを確認しましょう。そのあと、答えに小数点をつけましょう。
なおさきほど、「小数と整数のかけ算では、計算したあとに小数点を下におろす」と説明しました。小数と整数のかけ算では、小数と答えをくらべたとき、小数点の場所は同じになります。一方で小数と小数のかけ算では、小数点の場所がどこなのか考えなければいけません。
・小数のかけ算で小数点より下のケタ数が多くなる理由
小数と小数のかけ算をすると、小数点より下のケタが多くなります。なぜ、このようになるのでしょうか。それは、小数と小数のかけ算ではより小さい数が作られるからです。
たとえば、0.1と0.1のかけ算をすると、答えは0.01です。
- \(0.1×0.1=0.01\)
小数と小数のかけ算をすることによって、小さい数字が作られました。いずれにしても、小数どうしのかけ算では小さい数がうまれることを理解しましょう。そのため、小数と小数のかけ算では小数点より下のケタ数が多くなるのです。
おおよその数で計算すればミスを防げる
なお小数どうしのかけ算をするとき、ケタのミスをすることによって答えが違ってしまうことがあります。これを防ぐ方法はあるのでしょうか。
小数点の位置を間違えないようにするためには、おおよその数で計算しましょう。たとえば、以下の計算はどのようにすればいいでしょうか。
- \(25.3×2.85\)
この計算をすると、答えは72.105になります。答えが正しいかどうか大まかに確認するためには、かけ算をシンプルにしましょう。つまり25.3ではなく25、2.85ではなく3にします。数字を四捨五入して計算するのです。そうすると、以下のようになります。
- \(25×3=75\)
このように72.105と75の答えは似ているため、小数点の位置は正しいことが分かります。たとえば、出てきた答えが721.05であれば、あきらかに小数点の位置を間違えていると分かります。このようにして、答えが正しいかどうか事前に確認しましょう。
0が多い数字と小数のかけ算を簡単に計算する
なお算数の計算をするとき、0がたくさんある数字の計算をすることがあります。こうした整数と小数のかけ算をするとき、計算を簡単にするやり方があります。
難しい計算を避けるほど、計算ミスの確率が低くなって正しい答えを出せるようになります。そこで、どのようにして式をシンプルにするのか理解しましょう。かけ算では、0の数だけ小数点を右に移動させることができます。たとえば、以下の計算をしてみましょう。
- \(5000×0.04\)
この計算をするとき、0.04の小数点を右へ2つ移動させることができます。そのあと0をもつ数字に対して、右から2番目の場所に小数点を加えましょう。以下のようになります。

50.00について、小数点より下の0は省くというルールがあります。そのため、50.00ではなく50と記します。
いずれにしても、このようにすれば計算がとても簡単になります。\(5000×0.04\)ではなく、\(50×4\)という式に変えることができるのです。こうして、答えは200とわかります。
なぜ小数点を動かすことができるのでしょうか。たし算や引き算では無理ですが、かけ算(または割り算)であれば可能です。さきに説明した通り、かけ算ではケタを合わせなくてもいいからです。たとえば、以下のかけ算はすべて答えが同じです。
- \(1×1=1\)
- \(10×0.1=1\)
- \(100×0.01=1\)
このように、答えはすべて1です。また、小数点を移動させることによってすべて\(1×1\)の式に変えることができます。ケタを合わせる必要がないため、小数点の位置を変えて式を簡単にしましょう。
割合の計算が楽になるやり方
なお、この方法を理解すれば割合の計算が楽になります。割合では、ほぼ確実に小数を使うからです。たとえば、4%は0.04です。また12%は0.12です。そこで割合の計算について、ここまでの知識を使いましょう。
たとえば、以下の問題の答えは何でしょうか。
- 4000円の12%はいくらですか
この問題の式を作ると、\(4000×0.12\)となります。ただ、この式は複雑です。そこで先ほど説明した知識を使って、以下のように小数点を移動させましょう。
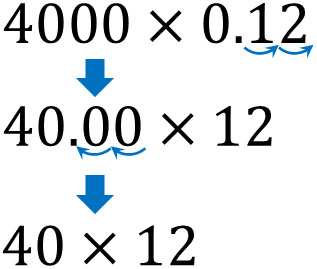
このようにすると、\(4000×0.12\)ではなく、\(40×12\)の式になります。そのため、答えは480円とわかります。
わたしたちの日常生活で割合の計算をすることは多いです。このとき、小数点を移動させて計算することができれば、はやく答えを出せるようになります。
小数のかけ算・筆算をする
1よりも小さい数をあつかうのが小数です。小数のかけ算をすることはよくあるため、どのようにかけ算をすればいいのか理解しましょう。
小数と整数のかけ算は難しくありません。一方、小数と小数のかけ算をするときは小数点の位置に気を付けましょう。小数点を右にいくら移動できるのかを確認し、正しい答えを出すといいです。このとき、大まかな数を利用して計算すれば、小数点の位置が正しいかどうか推測できます。
また0をもつ数字のかけ算では、式を簡単にすることができます。とくに割合の計算ではひんぱんに利用できる方法なので、やり方を理解しましょう。






