日常生活で比の計算をすることは多いです。例えば買い物では、比の計算ができないと安く買い物をすることができません。
比の計算をするとき、比の性質を理解しましょう。比には、同じ数をかけたりわったりしてもいいという性質があります。そのため大きい数であったり、数字に分数が含まれていたりする場合であっても、比を簡単にすることができます。
また比の計算で必ず理解するべき方法が比例式です。比例式は中学校や高校、大学の数学でもひんぱんに利用されます。特に文章問題を解くとき、比例式を必ず利用するようにしましょう。これにより、すべての比の問題を解けるようになります。
比の問題を解くとき、やり方があります。そこで比の性質を理解して、どのように比を簡単にしたり、比例式を利用したりすればいいのか理解しましょう。
もくじ
比とは何か:比の意味を理解する
比というのは、2つを比べることによって、どれだけ量に違いがあるのかを表します。例えば以下のように、バケツに2Lの水と5Lの水があるとき、比はいくらでしょうか。
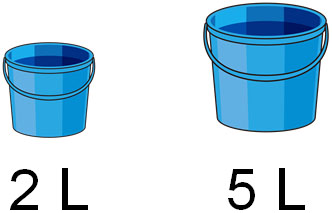
この場合、比は「2:5」です。また、比は分数で表すことができます。次に、以下のように長さの比を考えてみましょう。
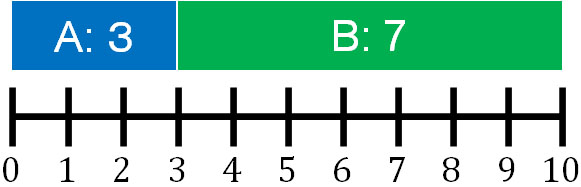
全体の長さは10です。これを3と7に分けました。AとBの長さを比べると、比は「3:7」になります。また全体の長さから考えると、Aの長さは\(\displaystyle\frac{3}{10}\)です。またBの長さは\(\displaystyle\frac{7}{10}\)です。これが、比を分数で表すことができる理由です。
次に、AとBの割合を計算してみましょう。Aを何倍すると、Bになるでしょうか。3(A)を基準として、\(☐\)倍すると7(B)になります。そのため、以下の式を作ることができます。
- \(3×☐=7\)
この式を解くと、Aを\(\displaystyle\frac{7}{3}\)倍すればBになるとわかります。つまり\(A×\displaystyle\frac{7}{3}=B\)です。
同様に、Bを基準とする割合も計算してみましょう。Bを何倍すると、Aになるでしょうか。7(B)を基準とし、て\(☐\)倍すると3(A)になります。そのため、以下の式を作ることができます。
- \(7×☐=3\)
この式を解くと、Bを\(\displaystyle\frac{3}{7}\)倍すればBになるとわかります。つまり\(B×\displaystyle\frac{3}{7}=A\)です。
比の値の計算方法
なお小学算数で比を学ぶとき、比の値を求めなければいけないことがあります。A:Bの比について、Bを基準にするときの割合を比の値といいます。
先ほど「A:B=3:7」の比について、Bを基準にすると\(B×\displaystyle\frac{3}{7}=A\)と表すことができると説明しました。このとき、\(\displaystyle\frac{3}{7}\)を比の値といいます。比の値を計算するとき、:の記号を÷に変えることで比の値をだせます。
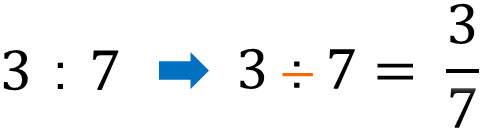
なお、比の値は重要ではありません。小学算数でテストの点を取るために覚えてもいいですが、中学や高校、大学の数学で比の値のがいねんを利用することはありません。
先ほどの例であれば、Aを\(\displaystyle\frac{7}{3}\)倍することでBを得られると解説しました。またBを\(\displaystyle\frac{3}{7}\)倍することでAを得られます。重要なのは、割合(分数)を利用して計算すれば、一方の量を計算できることです。
等しい比の計算と性質
なお比というのは、「Aを何倍すればBになるのか」を意味しています。または、「Bを何倍すればAになるのか」を意味します。例えば「A:B=1:3」であれば、Aを3倍すればBになります。また、Bを\(\displaystyle\frac{1}{3}\)倍するとAになります。
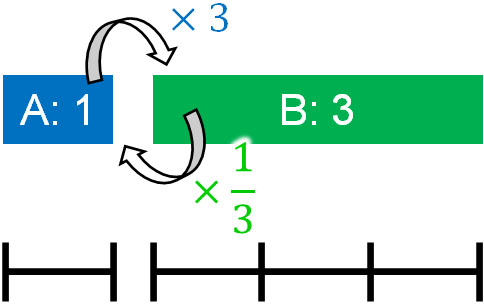
この性質を理解すると、AとBに対して同じ数をかける(または、わる)をしても同じ比になるとわかります。
例えば「A:B=1:3」について、AとBの両方の数字に対して2をかけましょう。そうすると、「A:B=2:6」になります。このとき、1:3と2:6は同じ比です。事実、Aを3倍するとBになります。またBを\(\displaystyle\frac{1}{3}\)倍するとAになります。
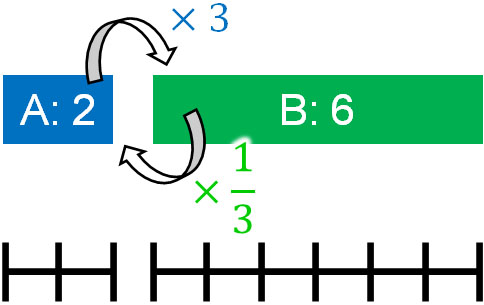
つまり「1:3」と「2:6」は同じ意味です。
また前述の通り、比に対して同じ数でわってもいいです。例えば「A:B=1:3」について、両方の数を3でわりましょう。そうすると、「A:B=\(\displaystyle\frac{1}{3}\):1」になります。このとき、1:3と\(\displaystyle\frac{1}{3}\):1は同じ比です。Aを3倍するとBになり、Bを\(\displaystyle\frac{1}{3}\)倍するとAになります。
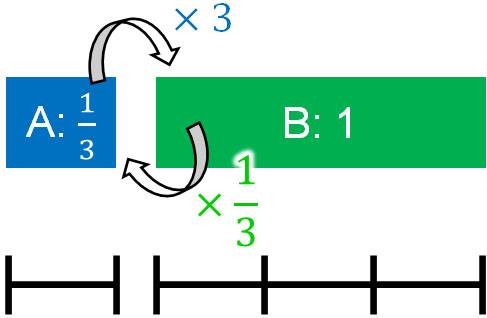
このように、同じ数を利用してかけたりわったりしても割合は同じです。なお等しい比は等号(=)を利用してつなぎます。例えば、以下のようになります。
- \(1:3=2:6\)
- \(1:3=\displaystyle\frac{1}{3}:1\)
比には、この性質があることを理解しましょう。
整数の比を簡単にする
次に、比を簡単にしましょう。数字が大きい場合、2つの関係性を理解しにくいです。例えば、以下の比は何を意味しているのかわかりにくいです。
- 72:108
そこで、同じ数でわることによって数字を小さくしましょう。公約数を利用することによってわると、整数の比を簡単にすることができます。先ほどの比であれば、36でわることによって以下のように整数の比を簡単にできます。
- \(72:108=2:3\)
実際に計算をするとき、2や3など小さい公約数を利用することで少しずつ比を簡単にしていきます。いずれにしても、比の性質を利用することによって整数の比を簡単にすることができます。
小数の比を簡単にする
次に小数の比を簡単にしましょう。小数の場合、両方に同じ数をかけることによって小数点をなくします。つまり10倍や100倍をすることによって、小数の比を整数の比に直しましょう。
例えば、以下の比を簡単にするにはどうすればいいでしょうか。
- \(0.3:0.8\)
この場合、両方の数を10倍しましょう。そうすれば3:8となり、比を簡単にできます。一方、以下の比を簡単にするにはどうすればいいでしょうか。
- \(0.12:0.04\)
まず、両方の数を100倍しましょう。そうすると12:4になります。ただ、12:4はさらに簡単にできます。そこで両方の数について4でわると、3:1になります。こうして小数の比を簡単にすることができます。
分数の比を簡単にする
次は分数の比を簡単にしましょう。分数の比を簡単にするためには、分母を消すようにします。つまり分母を比べ、最小公倍数をかけることで分母を消します。
例えば、以下の比はどのようにすれば簡単になるでしょうか。
- \(\displaystyle\frac{2}{3}:\displaystyle\frac{5}{4}\)
分母はそれぞれ3と4です。3と4の最小公倍数は12です。そこで、両方の分数に対して12をかけましょう。そうすると、以下のようになります。
- \(\displaystyle\frac{2}{3}:\displaystyle\frac{5}{4}=8:15\)
こうして、8:15と比を簡単にすることができました。
比例式を利用して計算する
比の性質を理解した後、比例式を学びましょう。比例式は非常に重要な計算方法であり、中学や高校、大学と数学の計算をするとき多くの場面で利用されます。そのため、必ず比例式の計算方法を理解しましょう。
比例式を利用すると、求めたい数字を簡単に計算できるようになります。先ほど、1:3と2:6が等しいことを説明しました。このとき、比の計算では「内側の数と外側の数をかけると、必ず同じ数字になる」という性質があります。
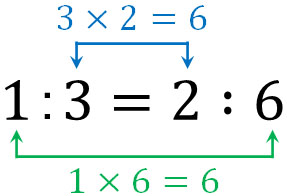
どのような比であってもこの関係が成り立ちます。例として、先ほど小数や分数の問題で計算した比を以下に記します。
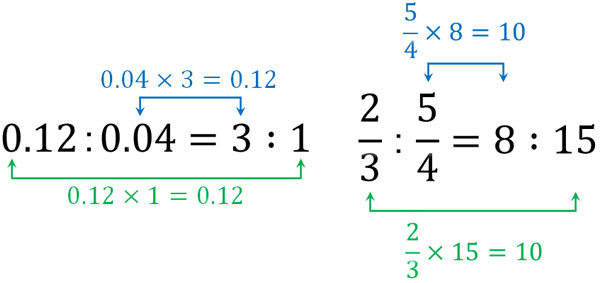
内側と外側をかけることによって、同じ答えになるとわかります。このように、比が等しくなる式を比例式といいます。
比例式は非常に便利であり、わからない数字があったとしても簡単に計算することができます。例えば、以下の\(☐\)に入る数字はなんでしょうか。
- \(3:5=0.2:☐\)
この比を満たす数字(\(☐\))を見つけるため、比例式を利用しましょう。比例式の内側と外側をそれぞれかけることによって、以下の式を作ることができます。
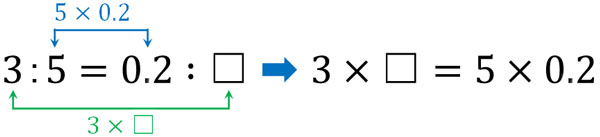
この式を解くと以下のようになります。
\(3×☐=5×0.2\)
\(3×☐=1\)
\(☐=\displaystyle\frac{1}{3}\)
こうして、\(☐\)に入る数字は\(\displaystyle\frac{1}{3}\)であるとわかります。
※参考までに、比例式は小学校で教えられないことがあります。ただ比例の計算はすべて比例式で行うことができ、比例式を利用するほうが圧倒的に計算が簡単で間違いも少ないです。そのため、比例式を利用して計算するようにしましょう。
比の文章問題を解く
比に関する文章問題では、必ず比例式を使うといいです。比例式を利用しない場合、問題を解くのが非常に難しくなります。一方で比例式を利用すれば、簡単に問題を解けるようになります。比例式を利用する場合、対応する比を作るだけで答えを出すことができるからです。
それでは、実際に文章問題を解いてみましょう。
・一方の数がわかっている場合
以下の問題を解いてみましょう。
- AとBの土地があり、土地の大きさの比は「A:B=2:5」です。Bの土地が800m2の場合、Aの土地の大きさはいくらですか?
土地の比はすでにわかっており、「A:B=2:5」です。またBの土地は800m2であるため、以下の図を作ることができます。
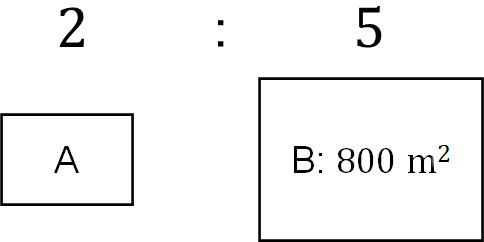
わからないのはAの土地の大きさです。そのためAの土地を\(☐\)とすると、以下の比例式を作ることができます。
- \(2:5=☐:800\)
必ず「A:B=2:5」となるため、Bの大きさがわかっているのであれば、この比例式を解くことによって答えを出すことができます。以下のようになります。
\(5×☐=2×800\)
\(5×☐=1600\)
\(☐=1600÷5\)
\(☐=320\)
こうして、Aの土地は320m2であるとわかります。
・合計がわかっている場合
一方、どちらか一方の大きさではなく、合計がわかっていることもあります。この場合についても、それぞれの大きさをだすことができます。比というのは、分数で表すことができると説明しました。そのため全体の大きさがわかれば、分数を利用することによって大きさを出せるのです。
例えば、以下の答えは何でしょうか。
- AとBの箱があり、重さの割合は「A:B=3:7」です。合計の重さが20kgの場合、Aの重さはいくらですか?
この問題では、AとBの両方とも箱の重さがわかりません。しかし、全体の重さはわかります。そのため以下のように図にすると、Aの割合が3でBの割合が7であるため、全体の割合は10になるとわかります。
- \(A+B=3+7=10\)
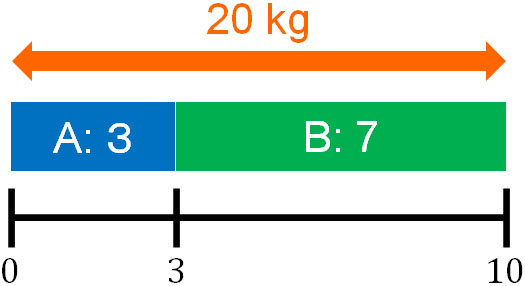
つまりAと全体の割合は3:10です。また全体の重さは20kgとわかっています。そのためAの重さを\(☐\)とすると、以下の比例式を作ることができます。
- \(3:10=☐:20\)
この比例式を解くと以下のようになります。
\(10×☐=3×20\)
\(10×☐=60\)
\(☐=60÷10\)
\(☐=6\)
こうして、Aの箱は6kgとわかります。参考までに、Aの重さを求めることができたため、Bの重さは14kgとわかります。
3つ以上の比を含む計算
ここまで、2つ比を利用して計算問題を解いてきました。ただ比の問題では、3つ以上の比を含むことがあります。例えば「A:B:C=2:4:9」のように、3つの数字を利用して比を表すのです。このような場合、どのように問題を解けばいいのか理解しましょう。
2つの比でも、3つの比でも、すべての数字を足すと全体の数になります。そこで全体の数に対して、割合がいくらなのかを考えて問題を解きましょう。例えば、以下の問題の答えは何でしょうか。
- AとBとCの角度の比は「1:3:5」です。Bの角度を求めましょう。
「A:B:C=1:3:5」です。また三角形の内角の和は180°であるため、すべての角度を足すと180°になります。そのため、以下の図を作ることができます。
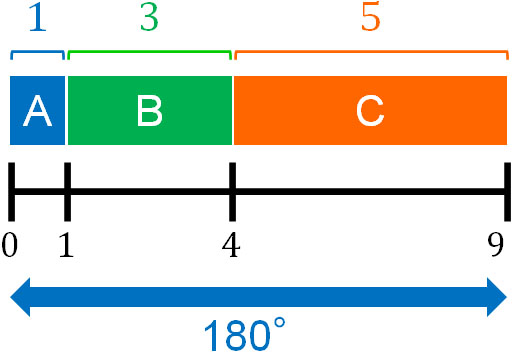
以下の計算より、全体の割合は9です。
- \(A+B+C=1+3+5=9\)
全体を9とするとき、Bと全体の比は3:9です。そのためBの角度を\(☐\)とすると、以下の比例式を作ることができます。
- \(3:9=☐:180\)
この比例式を解くと以下のようになります。
\(9×☐=3×180\)
\(9×☐=540\)
\(☐=540÷9\)
\(☐=60\)
答えは60°です。このように3つ以上の比を含む場合であっても、比例式を作るときは2つの比を利用しましょう。
なお、同様にAやCの角度を求めることもできます。全体を9とするとき、Aと全体の比は1:9です。そのため、\(1:9=☐:180\)という比例式を作れます。またCと全体の比は5:9です。そのため、\(5:9=☐:180\)という比例式を作れます。
Bの角度を求めたときと同じように解いてみると、答えはA=20°、C=100°となります。
比の性質を理解し、比例式を使って計算する
比を利用することは多く、比を理解していないと日常生活で困ることになります。そこで、比の性質やがいねんを理解しましょう。
比というのは、2つを比べるときに何倍になっているのかを表します。そのため両方の数字に対して、同じ数をかけたりわったりしてもいいです。同じ数のかけ算やわり算をしても、割合は同じだからです。
また比を学ぶとき、重要な計算方法が比例式です。すべての比の計算では、比例式を利用するようにしましょう。比例式は中学や高校、大学とすべての数学でひんぱんに利用されます。比例式を理解していない場合、比の問題を解くのが非常に難しくなります。
比の計算では、比の性質と比例式を用いた計算方法を理解しましょう。これによって比の計算ができるだけでなく、文章問題を解けるようになります。