日常生活でひんぱんに利用される言葉が平均です。平均を利用することによって、どれくらいの量があるのか理解できるようになります。
また平均を理解すれば、単位量当たりの大きさがわかるようになります。単位量当たりの大きさとは、ようは平均のことです。言葉はちがうものの、計算方法やがいねんは同じです。平均をだせば、単位量当たりの大きさをだすことができます。また平均を理解していない場合、単位量当たりの大きさを計算することはできません。
なお平均や単位量当たりの大きさでは、文章問題をだされることがひんぱんにあります。そのため計算方法だけでなく、文章問題から式を作れるようにならなければいけません。
買い物など、多くの場面で利用されるのが平均です。そこで平均と単位量当たりの大きさについて、計算方法や文章問題の解き方を解説してきます。
もくじ
平均とは何かを理解する
まず、平均とは何なのでしょうか。平均とは、異なる大小の数字を平らにそろえることを意味します。でこぼこしている状態を平らにするのが平均であると理解しましょう。
たとえば、以下のようにオレンジをもっているとします。
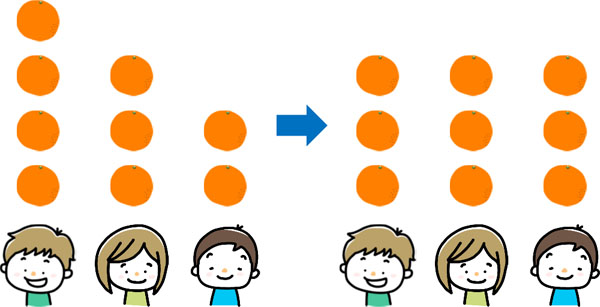
人によってもっているオレンジの数が異なります。そこで、全員が同じ数のオレンジをもてるように変えましょう。そうすると、一人3個のオレンジをもてるようになります。このように異なる数字について、一人(または一つの物)が同じ数になるように平らにすることが平均です。
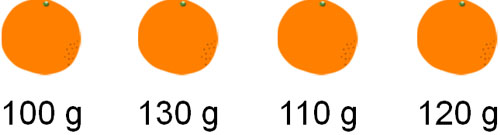
通常、人や物によって数字が異なります。たとえば、オレンジによってそれぞれ重さが違うのは普通です。そこで、オレンジ1個あたりの重さを知りたい場合、平均を利用します。
またテストをすると、人によってテストの点数が違います。そこでクラス全員のテストの点数について、一人当たり何点を取ったのか知りたいときに平均を利用します。全体に対して、一人(または一個の物)がいくらの数字をもっているのかを表すのが平均です。
平均を求める公式
それでは、どのようにして平均を求めればいいのでしょうか。先ほど、「一人当たり何個のオレンジをもつことができるのか」について平均をだしました。そこで人がオレンジをもっている状態ではなく、オレンジをもっていない状態を考えましょう。
以下のように、合計で9個のオレンジがあります。
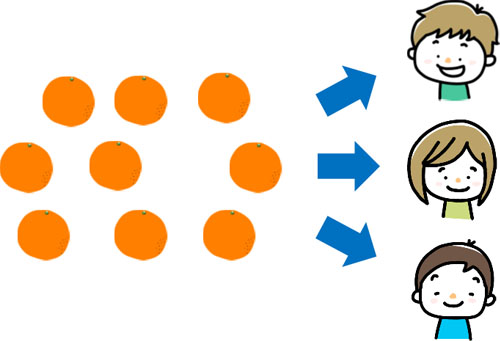
そこで、9個のオレンジを3人に対して同じ数を配る場合、一人は何個のオレンジをもつことができるでしょうか。このとき平均を利用にすることによって、一人3個のオレンジをもてることがわかります。
平均を計算するとき、最初に全体の数がいくつなのかを計算しましょう。先ほどの例であれば、オレンジ全体の数は9個です。
次に、全体の数を個数(または人数)でわりましょう。これによって、一個当たり(または一人当たり)の平均を得ることができます。先ほどの例であれば3人にオレンジを配るため、全体の数を3でわります。
- 9個 ÷ 3人 = 3(平均)
こうして、一人当たり何個のオレンジをもてることができるのか計算できます。そこで平均をだすとき、このオレンジの例題では以下の公式を利用します。
- 合計 ÷ 個数(または人数) = 平均
わる数が「個数」か「人数」かについては、与えられる問題によって違ってきます。ただ、この公式を覚える必要はありません。それよりも、どのように平均をだすのかイメージを理解しましょう。たとえば以下のオレンジについて、平均の重さは何でしょうか。

まず、全体の重さを計算しましょう。オレンジの重さを合計すると以下のようになります。
- \(100+130+110+120=460\)
これによって、4個のオレンジを合計した重さを計算できます。それではオレンジの合計の重さが460gのとき、4個のオレンジ一個当たりの重さはいくらでしょうか。
4個のオレンジを合計すると、重さが460gになります。つまり460gを4でわると、一個当たりのオレンジの重さをだせることがわかります。そのため、次の式を作りましょう。
- \(460÷4=115\)
こうして、オレンジ一個当たりの重さは平均115gになるとわかります。またこのように文章問題によって、わる数が「個数」になったり「人数」になったりします。
平均の計算は文章問題としてだされる
なお多くの場合、平均の計算は文章問題としてだされます。そこで、文章を読んで式を作れるようにしましょう。たとえば、以下の問題の答えは何でしょうか。
- Aさんは4秒で200cm歩きました。平均して1秒に平均何cm歩きましたか?
Aさんは合計で200cmを歩いています。そのため、合計の数は200cmです。また、Aさんが1秒に何cm歩いたのか知りたいです。Aさんは4秒を歩いているため、4でわればいいとわかります。
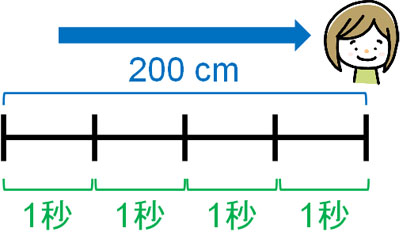
そのため、以下の式を作ることができます。
- \(200÷4=50\)
こうして、答えは50cmになります。このように、全体の数は何かを最初に見つけましょう。その後、わる数を見つけましょう。
公式を利用しても解くのは難しいです。公式を利用する場合、全体の数を個数でわります。ただ、個数がどれに当たるのかわかりにくいです。そこで、なれるまでは図を作ることによって答えをだすようにしましょう。
個数や合計を計算できる
なお平均を計算できるようになれば、個数や合計を計算できるようになります。先ほど解説した通り、合計と個数(または人数)を利用することによって平均をだせます。これはつまり、平均を利用して個数や合計を求めることができることを意味しています。
・合計を計算する
たとえば、以下の問題はどのように解けばいいでしょうか。
- Aさんは一歩で平均して50cm進みます。8歩を歩くと、何cm進みますか?
問題より、平均は一歩50cmです。また8歩を歩くことによって、合計で\(☐\)cm進むことになります。そのため、以下の図を作ることができます。
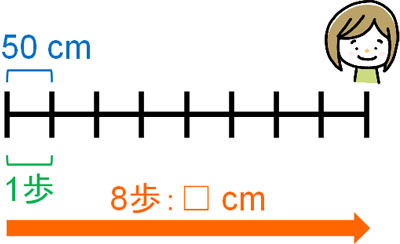
大人であっても、文章問題を解くときは図を作ります。もちろん図を描くのではなく、頭の中でこの図を作ります。公式を覚えたり、数字をみたりしても問題を解けるようになることはないため、なれるまでは図を作るようにしましょう。
またこのように図を作ると、一歩で平均50cm進むため、8倍すれば答えを出せるとわかります。そこで、以下の式を作りましょう。
- \(50×8=400\)
・個数を計算する
次は個数を計算してみましょう。たとえば、以下の問題はどのように解けばいいでしょうか。
- Aさんは一歩で平均して50cm進みます。300cm進んだ場合、Aさんは何歩を歩きましたか?
同じように、図を作りましょう。以下のようになります。
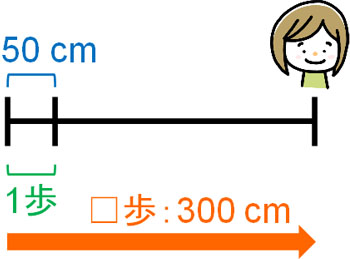
平均して、一歩50cmで進むことができます。その結果、合計で300cm進みました。そこで歩いた歩数を\(☐\)にすると、以下の式を作ることができます。
- \(50×☐=300\)
1歩で50cm進むため、\(☐\)歩を歩けば合計で300cm進むことになります。または、合計が300cmで平均が50cmであるため、以下の式を作ってもいいです。
- \(50=300÷☐\)
全体(300cm)から個数(\(☐\)歩)をわることによって、平均(一歩で50cm)を求めることができます。どちらの式であっても答えを出すことができます。
次に、式を変形しましょう。\(☐\)の値をだすためには、以下の式になります。
- \(☐=300÷50=6\)
こうして、6歩を歩くことによって合計で300cm進むことがわかります。
平均や合計、個数をだす公式はあるものの、これらの公式を覚えても意味ありません。それよりも、図を作ることによって式を作りましょう。
平均の応用問題を解く
なお平均を学ぶとき、応用問題がひんぱんにだされます。そこで、より複雑な計算問題を解けるようにしましょう。
たとえば、以下の問題の答えは何でしょうか。
- 男性6人のテストの平均点は8点であり、女性4人のテストの平均点は9点でした。10人での平均点はいくらですか。
平均の計算方法は同じであり、まずは全体の数に着目しましょう。男性6人で平均8点であるため、男性の合計点は\(6×8=48\)点です。一方、女性4人で平均9点であるため、合計点は\(4×9=36\)点です。そのため、10人全体の合計点は以下のように計算できます。
- \(6×8+9×4=84\)
10人で合計84点となります。そのため一人当たりの平均点をだすためには、10でわればいいとわかります。
- \(84÷10=8.4\)
こうして、一人当たりの平均点は8.4点であるとわかります。
単位量当たりの大きさでは平均をだす
ここまでの内容を理解すれば、単位量当たりの大きさを計算することができます。単位量当たりの大きさとは、平均を計算するのと意味が同じです。
先ほど、オレンジ1個あたりの平均の重さを計算しました。

計算式は以下になります。
- \(100+130+110+120=460\)
- \(460÷4=115\)
単位量当たりの大きさでは、1個が平均していくらの値になるのかを計算します。つまり平均の値をだせば、単位量当たりの大きさを出すことができます。
単位量当たりの大きさによって比較できるようになる
なぜ、平均を利用することで単位量当たりの大きさをだすことが重要なのでしょうか。それは、単位量当たりの大きさを利用することで比較することができるからです。
たとえば、以下はどちらが混んでいるでしょうか。
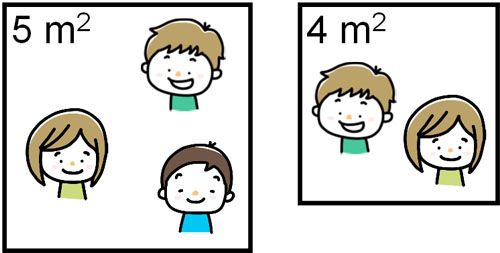
単位量当たりの大きさをだすことによって、2つを比べることができます。つまり1m2当たり、平均して何人がいるのかを計算することによって、どちらが混んでいるのか確認できます。
左図では合計で3人いて、面積が5m2です。そのため、1m2当たりに平均何人がいるのか計算するときの式は以下になります。
- \(3÷5=0.6\)
こうして、左図では1m2当たり0.6人がいるとわかります。
一方で右図では、1m2当たり何人がいるでしょうか。合計で2人いて、面積が4m2です。そのため、1m2当たりに平均何人がいるのか計算する式は以下になります。
- \(2÷4=0.5\)
こうして、左図では1m2当たり0.5人がいるとわかります。そこで2つを比べると、1m2当たり0.5人いるよりも、1m2当たり0.6人いるほうが混んでいるとわかります。このように、単位量当たりの大きさを利用することによって、どちらの数が大きいのか(または小さいのか)を判断できるようになります。
どっちを割るのかによって単位量当たりの大きさが異なる
なお平均を利用することで単位量当たりの大きさをだすとき、どっちの数を利用してわるのか注意しましょう。例として、以下の場面を考えてみましょう。
- 4つのオレンジを合計すると800円となる
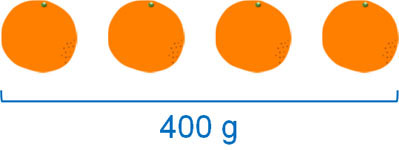
平均値(単位量当たりの大きさ)をだすとき、以下の2つの考え方があります。
- オレンジ1個当たりの重さはいくらか
- 1gはオレンジ何個分に当たるか
平均をだすとき、必ず個数(または人数)でわります。より具体的にいうと、「1つあたりの量を知りたい数」を利用してわります。
たとえば「オレンジ1個当たりの重さはいくらか」では、オレンジ1個につき何gになるのか知りたいです。そのため、オレンジの個数(4個)でわります。また合計が400gなので以下の式になります。
- \(400÷4=100\)
こうして、オレンジ1個当たりの重さは100gであるとわかります。
一方で「1gはオレンジ何個分に当たるか」では、1gにつきオレンジが何個含まれているのか知りたいです。そのため、グラム(400g)でわります。オレンジの合計は4個なので以下の式になります。
- \(4÷400=0.01\)
こうして、1gはオレンジ0.01個分に当たることがわかります。
重要なのは、わる数によって答えが異なることです。そこで、何でわればいいのか確認するようにしましょう。「1つ当たりの量を知りたい数」を利用し、わりましょう。
人口密度は単位量当たりの大きさで計算する
次に、人口密度を計算するようにしましょう。人口密度とは、1km2あたりの人口を指します。人口密度が高ければ、1km2に多くの人が住んでいることになります。それに対して人口密度が低ければ、1km2に少ない人数が住んでいることになります。
人口とは、住んでいる人数のことです。また1km2は面積を表します。なお人口密度では、「1つ当たりの量を知りたい数」は面積です。1km2に何人が住んでいるのか知りたいため、人口密度をだすときは面積を利用してわりましょう。たとえば、以下の町の人口密度はいくらでしょうか。
- 人口6000人、面積40km2
全体の人数は6000人です。また1km2の量(人の数)を知りたいため、面積でわりましょう。以下の式になります。
- \(6000÷40=150\)
こうして、1km2当たり150人が住んでいるとわかります。こうして、人口密度を計算することができます。
・人口密度を利用して人口を計算する
ちなみに、人口密度を利用して人口を計算することができます。先ほど、平均値を利用して個数や合計を計算しました。同じように考えて式を作れば、人口の計算ができます。たとえば、以下の町の人口は何人でしょうか。
- A町の面積は20km2あり、人口密度は30人
人口密度は30人のため、1km2当たり30人が住んでいます。また面積が20km2のため、20をかければいいとわかります。
- \(30×20=600\)
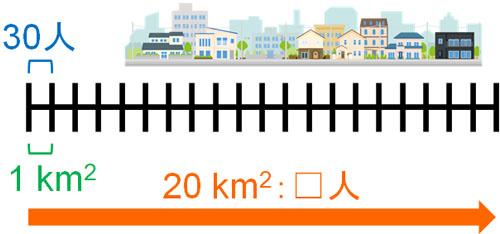
こうして、人口600人であるとわかります。
平均と単位量当たりの大きさを理解する
大人であれば、全員が平均を日常生活で使います。そのため平均の計算ができない場合、日常生活で困ることになります。たとえば買い物をするとき、平均を理解していないとどちらの商品が安いのか判断できません。
平均をだすには公式があるものの、公式を覚えても利用することはできません。どの値が合計であり、どの値が個数になるのか判断する必要があるからです。そこで図を作り、式を作るようにしましょう。
なお平均を理解すれば、単位量当たりの大きさを学ぶことができます。単位量当たりの大きさでは、どの数でわるのかに注意しましょう。「1つ当たりの量を知りたい数」を利用し、わり算をするといいです。またこの考え方を理解すれば、平均値をだすときにわる数が何になるのか間違えなくなります。
小学算数で平均と単位量当たりの大きさを学びます。これらを理解することによって、日常生活で役立てるようにしましょう。