分数の基本と種類：分子・分母の概念と真分数、仮分数、帯分数

分数ぶんすうは日常生活でひんぱんに利用します。そのため分数の考え方について理解していないと、日々の生活で計算することができません。

1よりも小さい数を表せるのが分数です。1つのものを複数に分けるとき、分数が利用されます。物を分けるときや買いものなど、分数を利用する場面は多いです。

なお分数には種類があり、真分数、仮分数、帯分数があります。中学数学や高校数学で帯分数を使うことはありません。しかし分数を学ぶとき、基礎を理解しなければいけません。そこで、まずはすべての分数の種類を学びましょう。

また分数では分子と分母を学ばなければいけません。そこで分数の種類や性質について解説していきます。

1 分数とは何か：1より小さい数
- 1.1 分子と分母の概念
- 1.2 わり算と分数の関係
2 真分数、仮分数、帯分数の違い
3 分数の概念を理解する

分数とは何か：1より小さい数

まず、分数とは何なのでしょうか。分数とは、1よりも小さい数を表せるやり方です。1よりも小さい数を表す方法として小数があります。分数についても、1より小さい数を表現できるのです。

なぜ分数を学ぶのでしょうか。それは、分数が便利だからです。たとえば、1つのケーキを5つに分ける場合、どのように表現すればいいでしょうか。

この場合、私たちは分数を使います。1つのケーキを5つに分けるため、1よりも小さい数になります。小さい数を取り扱うとき、分数を使うのです。以下のような数が分数です。

\(\displaystyle\frac{2}{3}\)、\(\displaystyle\frac{1}{10}\)、\(\displaystyle\frac{3}{8}\)

算数では分数を使う場面が多いです。

分子と分母の概念

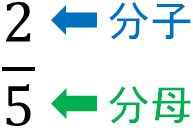
それでは、どのように分数を利用するのでしょうか。分数には分子ぶんしと分母ぶんぼがあります。この言葉の意味を覚えるようにしましょう。分数のうち、上にある数を分子といいます。また下にある数を分母といいます。以下のようになります。

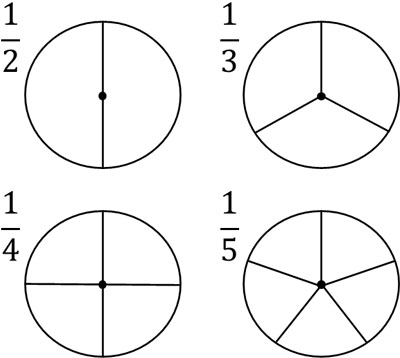
分母とは、1をいくつに分けるのかを表します。たとえば1つのケーキを3つに分ける場合、分母は3です。一方、1つのケーキを5つに分ける場合、分母は5です。

以下のように、何等分するのかによって分母が決まります。

一方で分子にはどのような意味があるのでしょうか。前に述べた通り、分けた後の数が分母です。それに対して、分けた後の数のうち、何個分かを表すのが分子です。

たとえばケーキを5つに分けた後、あなたが2つを食べれる場合、あなたが食べれるケーキの数は\(\displaystyle\frac{2}{5}\)です。一方でケーキを5つに分けた後、あなたが3つを食べれる場合、あなたが食べれるケーキの数は\(\displaystyle\frac{3}{5}\)です。

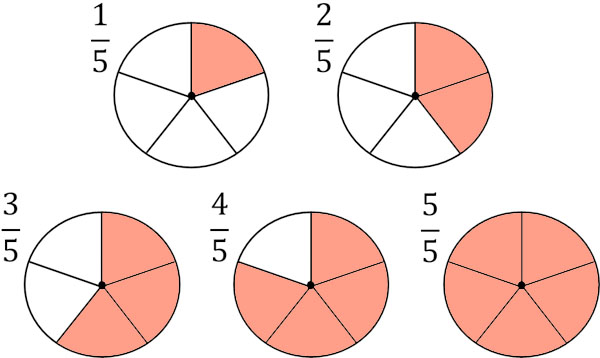
数を分けた後、何個分なのかを表すのが分子です。分数には必ず分子と分母があります。

わり算と分数の関係

それでは、分数は何を表しているのでしょうか。分数はわり算と意味が同じです。たとえば\(\displaystyle\frac{1}{4}\)では、1を4等分しています。つまり、\(1÷4\)と同じです。また\(\displaystyle\frac{3}{5}\)では、3を5つに分けます。そのため\(\displaystyle\frac{3}{5}\)は\(3÷5\)と同じ意味になります。

そのため、わり算と分数はたとえば以下のような関係になっています。

\(4÷9=\displaystyle\frac{4}{9}\)
\(13÷2=\displaystyle\frac{13}{2}\)
\(1÷3=\displaystyle\frac{1}{3}\)
\(5÷6=\displaystyle\frac{5}{6}\)

わり算は分数に変換へんかんできます。また、分数はわり算に変換できます。わり算を分数にする場合、わられる数は分子になり、わる数は分母になります。

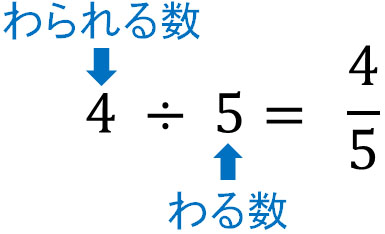
算数の計算でわり算と分数の関係は重要です。わり算を分数に変えることは多く、方法を理解するようにしましょう。

真分数、仮分数、帯分数の違い

なお分数にはいくつか種類があります。小学算数では以下の分数を学びます。

真分数しんぶんすう：分子の数が分母よりも小さい分数
仮分数かぶんすう：分子と分母が同じ分数、または分子の数が分母よりも大きい分数
帯分数たいぶんすう：整数と真分数を組み合わせた分数

たとえば、以下のようになります。

中学数学や高校数学など、高度な計算では帯分数を使うことはありません。通常、真分数と仮分数のみを利用することになります。ただ分数にはこれらの種類しゅるいがあり、まずはすべての種類を学ぶようにしましょう。

仮分数を整数に変換する

それでは、仮分数を整数に変換してみましょう。どのようにすれば、仮分数の形を変えることができるのでしょうか。

前述の通り、分数はわり算の式に変えることができます。そこで分数を整数にしたい場合、わり算の式に変換しましょう。たとえば、以下のようになります。

\(\displaystyle\frac{6}{2}=6÷2=3\)
\(\displaystyle\frac{20}{5}=20÷5=4\)

このように、仮分数を整数にすることができます。一方、わり切れない場合はどのように計算すればいいでしょうか。たとえば、\(\displaystyle\frac{14}{3}\)の整数はなんでしょうか。この場合、余りの数を利用して答えを出しましょう。以下のようになります。

\(\displaystyle\frac{14}{3}=14÷3=4\) あまり 2

このように、あまりの数を利用することによって分数を整数に変えることができます。

仮分数を帯分数に変える

次に、仮分数を帯分数に変換しましょう。帯分数とは、整数と真分数が混ざっている分数です。左に整数を記し、右に真分数を記します。また、帯分数は以下のようにたし算で考えることができます。

\(1\displaystyle\frac{2}{3}=1+\displaystyle\frac{2}{3}\)
\(3\displaystyle\frac{3}{7}=3+\displaystyle\frac{3}{7}\)

+の記号を省いたのが帯分数です。たとえば、\(1\displaystyle\frac{2}{3}\)は以下のようになります。

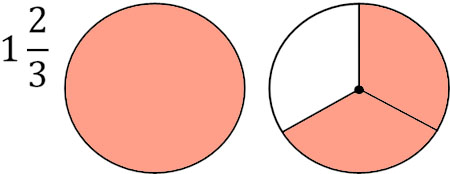
また前述の通り、仮分数では分母よりも分子の数が大きいです（または、分子と分母が同じ数）。つまり分子と分母が同じでない場合、仮分数は1よりも大きい数です。そのため、たとえば\(\displaystyle\frac{5}{4}\)は\(\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}\)に変えることができます。

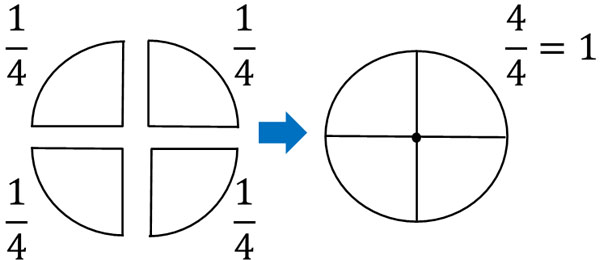
分子と分母が同じ分数は1です。以下のように、\(\displaystyle\frac{1}{4}\)が4つあると\(\displaystyle\frac{4}{4}\)になり、\(\displaystyle\frac{4}{4}=1\)であると分かります。

そこで、仮分数を整数と真分数に分けましょう。たとえば、\(\displaystyle\frac{5}{4}\)を帯分数にするにはどうすればいいでしょうか。まず、\(\displaystyle\frac{5}{4}\)を整数と真分数に分けましょう。以下のようになります。

\(\displaystyle\frac{5}{4}=\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}\)

また、\(\displaystyle\frac{4}{4}=1\)です。そのため、\(\displaystyle\frac{5}{4}\)は以下のように帯分数に変えることができます。

\(\displaystyle\frac{5}{4}=\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}=1\displaystyle\frac{1}{4}\)

このようにして仮分数から整数を取り出し、帯分数に変えることができます。

帯分数を仮分数に直すやり方

一方で帯分数から仮分数に変換するにはどのようにすればいいのでしょうか。先ほど、仮分数を整数に変える方法を解説しました。おさらいすると、以下のようになります。

\(\displaystyle\frac{6}{2}=6÷2=3\)
\(\displaystyle\frac{20}{5}=20÷5=4\)

整数から仮分数に変える場合、この計算の逆をしましょう。具体的には、整数と分母を掛けた答えを分子にしましょう。そうすれば、整数を分数に変えることができます。

たとえば、3を\(\displaystyle\frac{☐}{4}\)という形の分数に変えるにはどうすればいいでしょうか。この場合、整数である3と分母である4をかけ算し、でてきた答えを分子におきましょう。

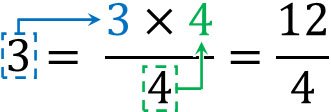
このように整数と分母を利用することで、整数を分数に変えることができます。なお\(\displaystyle\frac{12}{4}=12÷4=3\)となるため、分数への変換は正しいことが分かります。

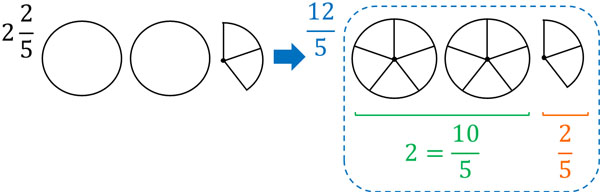
また、帯分数には整数の部分があります。たとえば、\(2\displaystyle\frac{2}{5}\)は\(2+\displaystyle\frac{2}{5}\)と同じ意味です。そこで、2を仮分数に変えましょう。2を\(\displaystyle\frac{☐}{5}\)の形にするため、整数と分母のかけ算をします。そうすると、以下のようになります。