分数のわり算をするとき、正しい方法があります。まず、分数のわり算をすることはありません。より正確にいうと、分数のわり算はすべて分数のかけ算に直す必要があります。つまり分数のわり算をするためには、「どのようにして分数のかけ算へ変えるのか」についての方法を理解する必要があります。
分数のわり算を分数のかけ算に変えるとき、必ず利用するのが逆数です。分子と分母をひっくり返すことによって、わり算からかけ算に変えることができます。
それでは、逆数とは何でしょうか。また、なぜ逆数を利用することによって分数のわり算が分数のかけ算になるのでしょうか。
算数の計算をするとき、理由を知ることは重要です。そこで分数のわり算をするとき、なぜ逆数がキーポイントになるのか解説していきます。
もくじ
分数での逆数とは何か
まず、逆数とは何でしょうか。分数のわり算を学ぶ前に、すべての人が逆数を教わることになります。逆数とは、分子と分母を裏返しにした数字を指します。
例えば、\(\displaystyle\frac{3}{4}\)の逆数は\(\displaystyle\frac{4}{3}\)です。
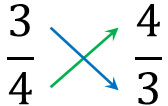
分子と分母を入れ替えるだけなので、逆数の概念は簡単です。
ちなみに、3の逆数は\(\displaystyle\frac{1}{3}\)です。3は\(\displaystyle\frac{3}{1}\)です。そのため、\(\displaystyle\frac{3}{1}\)の逆数は\(\displaystyle\frac{1}{3}\)になります。整数であっても逆数があります。
逆数とは、かけて1になる数をいう
逆数について、より正確にいうと「かけて1になる数」を指します。つまり、ある数をかけて答えが1になる場合、その数を逆数といいます。
先ほど、\(\displaystyle\frac{3}{4}\)の逆数は\(\displaystyle\frac{4}{3}\)であると解説しました。この理由として、\(\displaystyle\frac{3}{4}\)と\(\displaystyle\frac{4}{3}\)をかけると答えが1になるからです。
- \(\displaystyle\frac{3}{4}×\displaystyle\frac{4}{3}=1\)
ただ逆数を見つけるとき、「かけ算をして1になる数」という説明では理解しにくいです。そこで、「分子と分母をひっくかえした数が逆数」と覚えましょう。
分数のわり算では、逆数を利用して分数のかけ算へ変換する
それでは、分数のわり算をするときはどのようにすればいいのでしょうか。分数のわり算では、必ず逆数を利用することになります。よりくわしくいうと、分数のわり算では、わる数を逆数に直してかけ算にしましょう。
例えば、以下の計算はどのようにすればいいでしょうか。
- \(\displaystyle\frac{2}{3}÷\displaystyle\frac{5}{4}\)
この場合、分数のかけ算に変えた後に\(\displaystyle\frac{5}{4}\)を逆数にしましょう。以下のようになります。
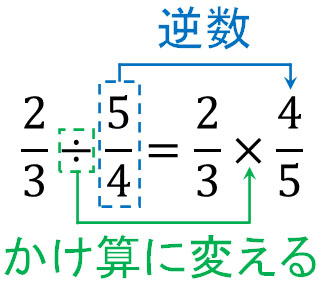
このように逆数を使うことによって、すべての分数のわり算は分数のかけ算に直すことができます。分数のわり算をする人はいません。必ず分数のわり算を分数のかけ算に変換しましょう。そうしなければ、高確率で計算ミスが起こります。
なお逆数を利用して式を変えた後、計算方法は一般的な分数のかけ算と同じです。分子同士、分母同士のかけ算をすることで答えを出しましょう。また約分できる場合、分数の数を小さくしましょう。
なぜ分数のわり算では逆数のかけ算に変えれるのか
それでは分数のわり算をするとき、なぜ逆数のかけ算に変えることができるのでしょうか。多くの人は「分数のわり算では逆数を利用する」と理解しています。しかし、その理由を説明できません。そこで、この理由を理解しましょう。
分数のわり算で逆数を利用してもいい理由について、いくつか説明する方法があります。そこで、最初は直感的に理解する方法について解説していきます。
まず、以下の問題の答えは何でしょうか。
- \(8÷2\)
この問題の答えは4です。では、なぜ4が答えになるのでしょうか。考え方としては以下の2通りがあります。
- 8を2等分したあとの答えは何か
- 8には2がいくつ含まれるか
このうち、「8には2がいくつ含まれるか」の考え方を使って話を進めていきましょう。
次に、2には\(\displaystyle\frac{1}{2}\)はいくつ含まれているでしょうか。この質問は\(2÷\displaystyle\frac{1}{2}\)と意味が同じです。確認すると、2には4つの\(\displaystyle\frac{1}{2}\)が含まれます。そのため、答えは4であると分かります。
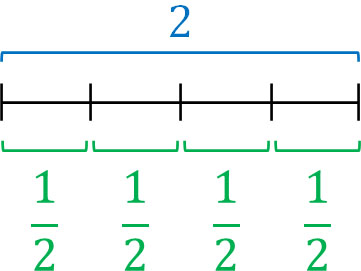
重要なのは、ここまで解説した式はすべて「逆数を利用することでかけ算の分数に変えることができる」という事実です。
- \(8÷2=\displaystyle\frac{8}{1}×\displaystyle\frac{1}{2}=4\)
- \(2÷\displaystyle\frac{1}{2}=\displaystyle\frac{2}{1}×\displaystyle\frac{2}{1}=4\)
このように図にすると、逆数を利用しても問題ないことを直感的に理解できます。
逆数のかけ算が有効であると理解する
それでは、より複雑な分数のわり算ではどのように考えればいいのでしょうか。例えば、以下の計算はどのようにすればいいでしょうか。
- \(\displaystyle\frac{1}{2}÷\displaystyle\frac{1}{4}\)
すべてのわり算は分数に変換できます。例えば、\(1÷3\)は以下のようになります。
- \(1÷3=\displaystyle\frac{1}{3}\)
これは、\(\displaystyle\frac{1}{2}÷\displaystyle\frac{1}{4}\)のような分数同士のわり算であっても同様です。そこで、以下のように分数の中に2つの分数を作りましょう。
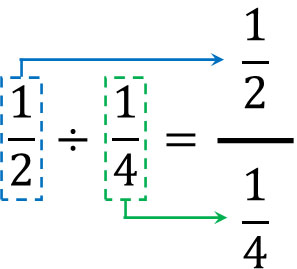
分数の中に分数があることを奇妙に思う人がいるかもしれません。その場合、小数で考えてみましょう。以下のように、それぞれの分数を小数に変えることができます。
- \(\displaystyle\frac{1}{2}=1÷2=0.5\)
- \(\displaystyle\frac{1}{4}=1÷4=0.25\)
そのため、以下のようになります。
- \(\displaystyle\frac{1}{2}÷\displaystyle\frac{1}{4}=0.5÷0.25=\displaystyle\frac{0.5}{0.25}\)
このように小数で考えると、\(\displaystyle\frac{0.5}{0.25}\)という分数があるのは普通です。また\(\displaystyle\frac{1}{2}=0.5\)であり、\(\displaystyle\frac{1}{4}=0.25\)です。そのため、以下のようになります。
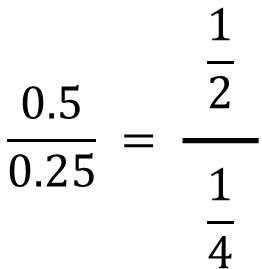
いずれにしても、このように分数の中に分数があるケースがあります。
次にこの分数に対して、逆数を利用して分母を1にしましょう。分数には「分子と分母に対して同じ数をかけたとしても、答えは同じになる」という性質があります。この性質については、通分ですでに習っています。そこで分母の逆数を分子と分母にかけましょう。以下のようになります。
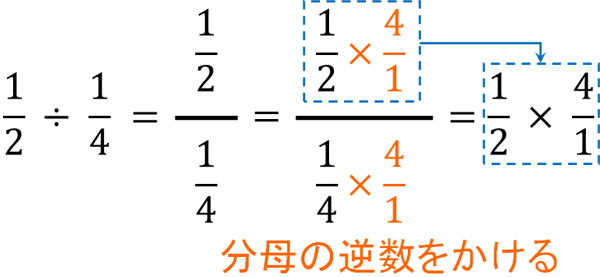
分母の逆数をかけることにより、分母は1になります。通常、分母にある1は省きます。そのため、分母は消えます。次に分子に着目しましょう。分子では、分母の逆数をかけた式ができます。
このように確認すると、逆数を利用することによって、分数のわり算を分数のかけ算へ変えられることが分かります。なお小学生に対して逆数の説明をする場合、この方法がもっとも一般的に利用されます。
前述の通り分数のわり算では、必ず分数のかけ算へと変換します。そのため、なぜ逆数を利用すれば分数のわり算を分数のかけ算に直すことができるのか理解しましょう。
分数のわり算では逆数を利用する
算数ではたし算、ひき算、かけ算、わり算を学びます。この中でも、分数のわり算はやり方が通常とは異なります。分数ではわり算をすることがなく、必ずかけ算の分数に変えなければいけません。
分数のわり算を分数のかけ算に直すとき、逆数を利用しましょう。分数を逆数にしたあと、わり算の記号をかけ算の記号に変えます。そうすれば、逆数を利用することでわり算の式をかけ算の式に変えることができます。
なお、多くの人は「なぜ逆数を利用することでわり算をかけ算に変えることができるのか」の理由を知りません。そこで、この理由を学びましょう。理由を理解すれば、納得した状態で計算することができます。
分数のわり算をすることはありません。必ずかけ算の式に直します。この性質を理解して、分数のわり算を計算しましょう。