何かをかぞえるとき、私たちは単位を利用します。主に利用される単位としては、長さ・重さ・面積・体積・容積があります。これらの単位はそれぞれ異なります。
また、長さを示す単位であったとしても、いくつか種類があります。そのため長さや重さ、面積、体積、容積の単位について、単位を変えられるようにしましょう。単位を変えることは日常生活でもひんぱんにあるため、これができないと日々の生活で困ることになります。
それでは、単位にはどのような種類があるのでしょうか。また、どのように単位換算をすればいいのでしょうか。これらについて解説していきます。
長さの単位と単位換算
単位には種類があります。そこで、まずは長さの単位から理解するようにしましょう。長さの単位はひんぱんに利用されるからです。
長さの単位としては、主に以下が知られています。
- mm(ミリメートル)
- cm(センチメートル)
- m(メートル)
- km(キロメートル)
これらの長さの単位をすべて覚えるようにしましょう。また、長さの単位では以下の関係性があります。
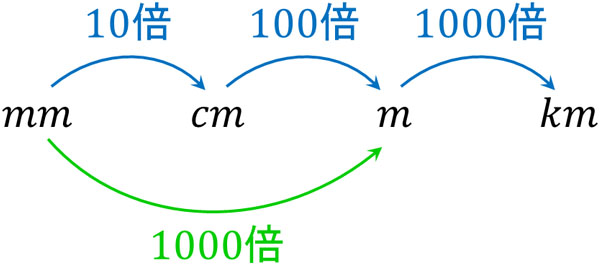
mmを10倍すると、cmになります。つまり、10mm=1cmです。またcmを100倍すると、mになります。そのため100cmは1mです。mを1000倍すると、kmになります。1000mは1kmです。
・長さの単位換算
それでは、3kmは何メートルでしょうか。1km=1000mです。そのため、1000倍すればkmをmに変えることができます。つまり、3kmは3000メートルです。
また、32mmは何センチでしょうか。10mm=1cmです。そのため、10でわるとmmがcmになるとわかります。つまり、32mmは3.2cmです。
単位換算をするとき、何倍すればいいのか理解する必要があります。覚え方としては、k(キロ)とm(ミリ)の意味を理解しましょう。kは1000倍することを意味します。そのため1km=1000mです。1m(メートル)を1000倍すれば、1 k(キロメートル)になるのです。
一方でm(ミリ)は\(\displaystyle\frac{1}{1000}\)倍を意味します。そのため1m(メートル)を\(\displaystyle\frac{1}{1000}\)倍すると、1mm(ミリメートル)になります。
・mmとcm、mの関係を理解する
なおmmは非常に小さい距離(長さ)です。短い長さを調べるとき、私たちが日常生活でひんぱんに利用する単位はcm(センチ)です。事実、三角形や四角形の辺の長さを計算するとき、ほとんどの問題は長さの単位がcmです。
そこで長さを理解しやすくするために、mm(ミリ)とm(メートル)の間にcm(センチ)があります。cmを利用することによって、どれくらいの長さになるのかわかりやすくなります。例えば125mmよりも、12.5cmのほうが理解しやすいです。数字が小さくなれば、私たちはすぐに理解できるのです。
ほとんどの場合、単位は1000倍ごとになります。ただcmについては例外であり、mmやmを何倍すればcmになるのか覚えましょう。
重さの単位は1000倍ごとになる
長さと同じように、ひんぱんに利用される単位が重さです。重さには主に以下の単位が使用されます。
- mg(ミリグラム)
- g(グラム)
- kg(キログラム)
- t(トン)
特にmgやg、kgは日常生活で毎日使います。そのため、必ず覚えなければいけない単位です。それぞれ、以下の関係になっています。
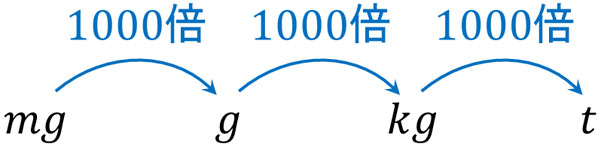
重さの単位については、1000倍することによって単位が変化します。mgを1000倍するとgになります。またgを1000倍するとkgになります。kgを1000倍するとtになります。
先ほど解説した通り、k(キロ)は1000倍を意味します。そのためg(グラム)に対して、kg(キログラム)は1000倍になります。一方でm(ミリ)は\(\displaystyle\frac{1}{1000}\)倍を意味します。そのため、g(グラム)に対して\(\displaystyle\frac{1}{1000}\)倍するとmg(ミリグラム)になります。
・重さの単位換算
それでは、重さの単位換算はどのようにすればいいのでしょうか。長さと同じように、単位の関係性から単位換算するようにしましょう。
例えば、5.2kgは何グラムでしょうか。1kg=1000gです。つまりkgをgにするためには、1000倍すればいいとわかります。そのため、5.2kgは5200gです。
一方で420mgは何グラムでしょうか。1000mg=1gです。つまり\(\displaystyle\frac{1}{1000}\)倍すれば、mgをgに変えることができます。そのため、420mgは0.42gです。単位換算をするときは「1kg=1000g」「1000mg=1g」「1000kg=1t」などのように、単位同士の関係を利用して答えをだすようにしましょう。
面積の単位は種類が多い
なお長さの単位を学べば、面積の単位を理解できるようになります。たてと横の長さをかけることによって面積をだすことができるからです。なお面積の単位は種類が多く、以下のような単位が利用されます。
- cm2(平方センチメートル)
- m2(平方メートル)
- a(アール)
- ha(ヘクタール)
- km2(平方キロメートル)
それぞれの関係性は以下のようになります。
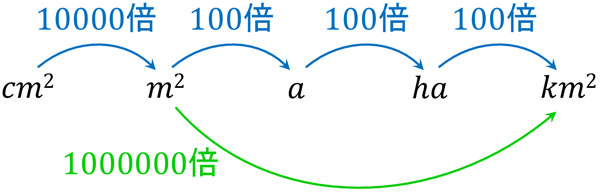
面積の単位換算は少し複雑になります。ただ、長さの単位換算ができれば難しくありません。まず、cm2をm2にするにはどうすればいいでしょうか。何倍すればいいのか覚えていない場合であっても、面積の単位換算は可能です。
以下のように、面積はたてと横の長さをかけることによってだします。
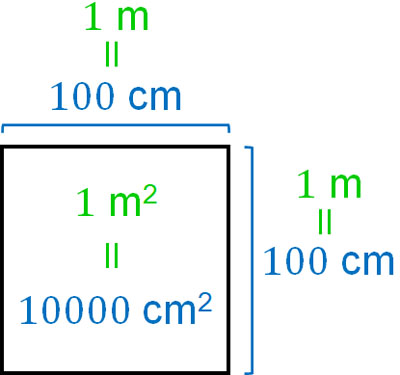
1m2というのは、一つの辺が100cmの正方形の面積を意味します。そこで面積を計算すると、1m2=10000cm2であるとわかります。
同じように考えると、1km=1000mです。1km2というのは、一つの辺が1000mの正方形の面積を意味します。そこで面積を計算すると、1km2=1000000m2であるとわかります。
・a(アール)やha(ヘクタール)とは何か
なお面積の単位にはa(アール)やha(ヘクタール)もあります。通常、面積の単位としてcm2(平方センチメートル)、m2(平方メートル)、km2(平方キロメートル)を利用します。ただ農地などでは、a(アール)やha(ヘクタール)を利用することがあります。
ha(ヘクタール)は多くの人が利用します。一方、a(アール)はほぼ利用されないため重要ではありません。
ただ面積の単位換算をするとき、aを理解していると便利です。m2を100倍すればaになります。aを100倍すればhaになります。haを100倍すればkm2になります。このように、100倍ずつになっています。
・面積の単位換算
それでは、0.0003m2は何cm2でしょうか。1m=100mです。そのため、1m2=10000cm2です。つまりm2をcm2にするためには、10000倍すればいいとわかります。そのため、0.0003m2は3cm2です。
一方、52000m2は何haでしょうか。10000m2=1haです。つまりm2をhaにするためには、\(\displaystyle\frac{1}{10000}\)倍すればいいとわかります。そのため、52000m2は5.2haです。
体積と容積では単位が異なる
次に体積と容積の単位を理解しましょう。体積については長さの単位であるcmやmを利用します。体積で主に利用される単位は以下です。
- cm3
- m3
また体積の場合、たて・横・高さをかけるので以下のような関係になります。
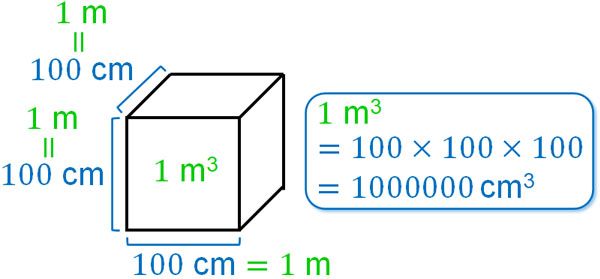
つまり、1m3=1000000cm3になります。
・容積を表す場合、単位が変わる
一方で容積を表す場合、単位が変わります。また、いくら液体が入っているのかを表す単位には種類が複数あります。体積とは異なり、容積では以下の単位を利用します。
- mL(ミリリットル)
- dL(デシリットル)
- L(リットル)
- kL(キロリットル)
重要なのは、1cm3=1mLであることです。つまり1mLとは、たて・横・高さが1cmになる液体の容量(容積)を意味します。体積ではcm3を利用するものの、容積ではmLを利用することに注意しましょう。また、これはkLでも同様です。1m3=1kLです。
体積も容積も計算方法は同じです。ただ、体積と容積では単位が違うことに注意しましょう。なお、容積の場合、単位は以下のような関係になっています。
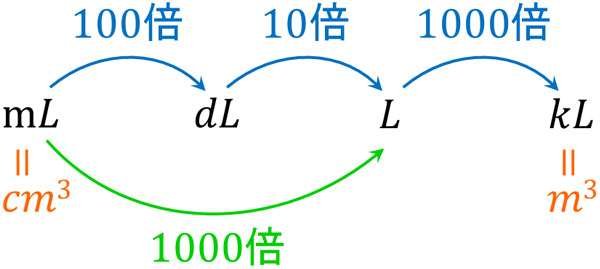
これまで説明した通り、k(キロ)は1000倍を意味します。そのため、1kL=1000Lです。また、m(ミリ)は\(\displaystyle\frac{1}{1000}\)倍を指します。そのため、1L=1000mLです。
なお容積ではdL(デシリットル)という単位も利用されます。mLを100倍すれば、dLになります。そのため、1dL=100mLです。またdLを10倍すれば、Lになります。そのため、1L=10dLです。
・体積と容積の単位換算
次に単位換算をしましょう。例えば、3500000cm3は何m3でしょうか。1000000cm3=1m3です。つまり、\(\displaystyle\frac{1}{1000000}\)倍すれば、cm3をm3に変えることができます。そのため、3500000cm3は3.5m3です。
一方、0.63Lは何dLでしょうか。1L=10dLです。つまり、10倍すれば、LをdLに変えることができます。そのため、0.63Lは6.3dLです。
ちなみに、日常生活では体積よりも容積をひんぱんに利用します。以下のように、日常生活の多くの場面で容積の単位を確認できます。

容積の単位を理解していない場合、日常生活で困ることになります。そこで容積の単位を覚え、単位換算できるようにしましょう。
単位換算に慣れる
長さや重さ、面積、体積、容積の単位を学ぶと、多くの単位があるとわかります。また、すべての単位を覚えなければいけません。
このとき、なぜ単位換算が重要になるのでしょうか。この理由として、単位換算をしなければどちらの数が大きいのか(または小さいのか)を判断できないからです。例えば、以下の数字はどちらが大きいでしょうか。
- 120cm
- 1.5m
1.5mをcmに直してみましょう。そうすると、1.5m=150cmになります。つまり、1.5mは120cmよりも大きいです。このように同じ単位にそろえると、数字の大きさを判断できるようになります。そこで、単位換算に慣れるようにしましょう。
単位を覚え、単位換算できるようにする
数字の大小だけでは、大きいのか小さいのか判断できません。そのため、私たちは単位を利用します。歩くにしても、1mと1kmでは長さが大きく異なるのです。
単位で重要になるのが長さや重さ、面積、体積、容積です。これらの単位は日常生活でひんぱんに利用されるため、必ず覚えるようにしましょう。それに加えて、単位換算できるようになることが重要です。単位換算できれば、数字の大小を比べられるようになります。
小学算数で学ぶ単位は日常生活で役に立ちます。そこでどのような単位があるのか、またどう単位換算すればいいのか理解しましょう。