立方体・直方体・角柱・円柱の展開図

平面の図形を組み立てると、立体の図形にすることができます。またハサミを利用して立体の図形をバラバラにすると、平面に変えることができます。平面図形と立体図形はたがいに関係があるのです。

立体図形を平面図形に変えたものを展開図といいます。また展開図を利用して、立体図形を作ることができます。算数では展開図の問題がだされます。具体的には立方体・直方体・角柱・円柱の展開図を理解しましょう。

展開図を確認すれば、辺の長さを計算することができます。また、立体の面積や体積を計算することもできます。

それでは、どのように展開図の問題を解けばいいのでしょうか。小学算数で重要な展開図について解説していきます。

展開図とは何か：立方体の展開図

展開図とは、立体を切り開いて平面にした図を指します。例えば、以下は立方体の展開図です。

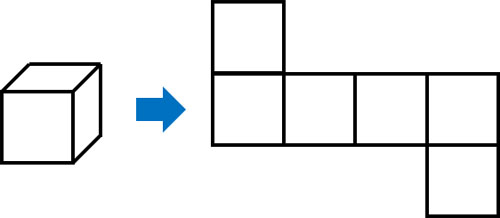
正方形が6つあると立方体になります。そこでハサミを利用して立方体を切り開くと、このように平面図形に変えることができます。

4パターンある立方体の展開図

立方体の図形では、「どの展開図が立方体になるのか」を問う問題がだされます。例えば以下の展開図のうち、どちらで立方体を作れるでしょうか。

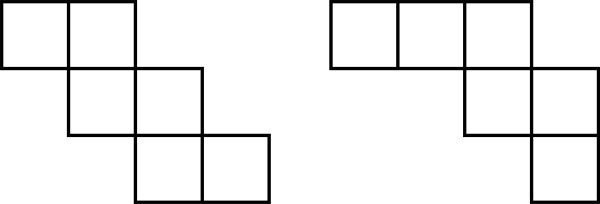
正解は左の図です。この問題は難しく、頭の中で想像しなければ解くことができません。

なお立方体の展開図は全部で11種類あります。また種類を確認すると、4パターンにわけることができます。以下の4パターン（11種類）です。

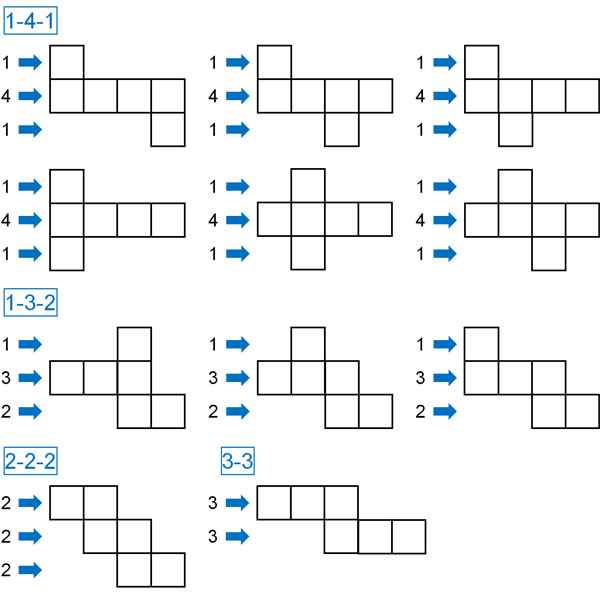
このように何枚の正方形がどの場所に配置されているのかによって、組み立てるときに立方体を作れるかどうかを判断できます。

ただ、11種類を覚えるのは大変です。また立方体の展開図の問題は重要ではありません。11パターンを覚えれば問題を解けるものの、覚えていない場合は問題を解くのが難しいです。そのため、立方体の展開図の問題が解けなかったとして問題ありません。

重要なのは直方体の展開図：辺の長さを求める

前述の通り、立方体の展開図をみたとき、どの展開図で立方体を作れるのかを理解する必要はありません。一方、直方体や角柱、円柱の展開図を理解するのは重要です。ハサミを利用してこれらの図形を切り開き、展開図にしたとき、どのような平面図形になるのか理解するようにしましょう。

まずは直方体の展開図を確認していきましょう。正方形を利用して作ることのできる立体が立方体です。一方、長方形を利用して作ることのできる立体が直方体です。

直方体を展開図にすると、以下のようになります。

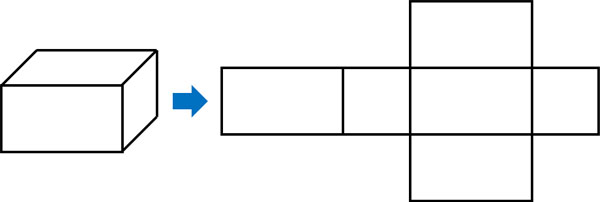
立方体の場合、すべての辺の長さが同じであるため、どのような展開図になるのか考えるのはむずかしいです。一方で直方体では、長方形を利用するので理解しやすいです。

直方体の展開図をみて、どこがたて、横、高さになるのでしょうか。以下のようになります。

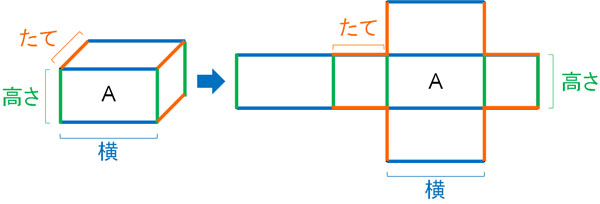
展開図で辺の長さがわかれば、直方体での辺の長さがわかります。そこで、直方体のたて・横・高さのうち、展開図のどこに対応するのか理解しておきましょう。

なおたてと横の長さがわかれば、長方形の面積を計算することができます。また、たて・横・高さがわかれば、直方体の体積を計算することができます。つまり、展開図を利用して長方形の面積や直方体の体積をだすことができます。

角柱の展開図を理解する

直方体の展開図を学べば、角柱の展開図についても理解できるようになります。角柱とは、2つの底面が三角形や四角形などの多角形になっている立体を指します。以下が角柱になります。

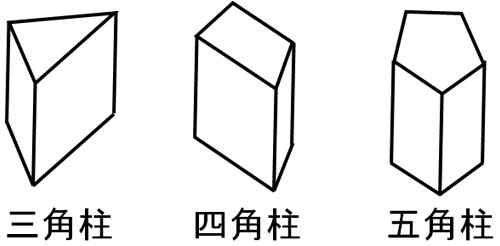
底面が三角形の場合、三角柱と呼ばれます。また底面が四角形の場合、四角柱と呼ばれます。立方体や直方体は四角柱でもあります。

直方体と同じように、ハサミを利用して角柱を切り開き、展開図を作ってみましょう。例えば三角柱の展開図は以下のようになります。

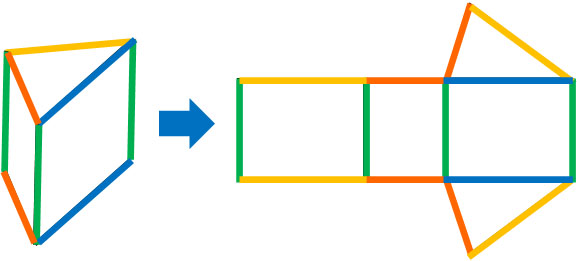
例えば展開図での緑色の線の長さを確認すれば、三角柱の高さを知ることができます。立体を切り開いた図が展開図であるため、展開図での辺の長さがわかれば、角柱での辺の長さを知ることができます。

ただ辺の長さを知るためには、展開図の辺と立体の辺を対応できるようにしなければいけません。そこで展開図を組み立てて立体にするとき、対応する場所を確認するようにしましょう。

円柱の展開図では円周が重要

立体の展開図では円柱も学びます。以下のように、底面が円になっている立体が円柱です。

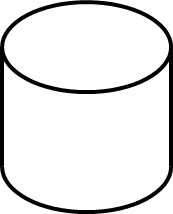
角柱では底面が三角形や四角形などの多角形であったものの、円柱では円になるのです。それでは、円柱の展開図はどのようになるのでしょうか。

以下が円柱の展開図です。

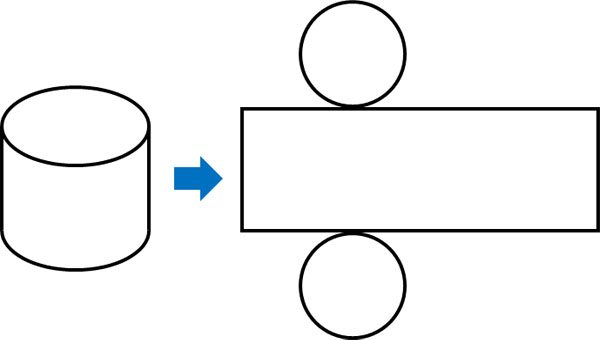
このように、円柱の展開図では必ず円と長方形ができます。

円柱の展開図で最も重要な要素として、「底面の円周は必ず長方形の横の長さになる」ことがあります。図を確認すると、以下のように展開図では底面の円周と長方形の横の長さが同じでなければいけません。

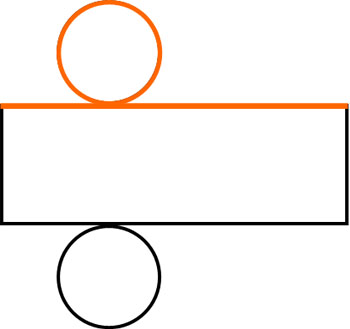
もし底面の円周と長方形の横の長さが同じでない場合、円柱を作ることができません。長さがあまったり足りなかったりするからです。なお円柱の高さ（長方形のたての長さ）がわかっている場合、底面の円周を利用することによって、長方形の面積を計算できます。

円柱の展開図で重要な要素が底面の円周と長方形の横の長さの関係です。この関係を理解するようにしましょう。

小学算数で展開図の問題を解く

小学算数では立体図形を学びます。立体図形は平面図形に変えることができ、平面図形は立体図形に変えることができます。具体的には、ハサミを利用して立体図形を切り開くとき、できる平面図形を展開図といいます。

立方体の展開図は重要ではありません。一方、直方体の展開図は重要です。このとき展開図の辺と直方体の辺を対応できるようにしましょう。

また展開図の問題では、角柱や円柱もだされます。底面が多角形の場合、角柱とよばれます。直方体と同じように、角柱とその展開図についても辺の長さを対応できるようにしましょう。また底面が円の場合、円柱とよばれます。円柱の展開図では、底面の円周と長方形の横の長さの関係が重要です。

展開図の問題では、これらのポイントを学びましょう。図形の性質を覚えることによって、辺の長さをだせるようにしましょう。