分数のかけ算：分子同士・分母同士のかけ算と約分

小学校の算数では分数を学びます。分数の計算をするとき、かけ算をします。分数のかけ算はたし算や引き算に比べて簡単です。通分をすることによって、分母をそろえる必要がないからです。

ただ、かけ算をするときは約分をする必要があります。また分数のかけ算では、必ず帯分数ではなく仮分数にしなければいけません。

なお約分できる場合、かけ算をする前に約分をするのが一般的です。そのほうが計算ミスを少なくできるからです。

たし算や引き算より簡単であるものの、分数のかけ算についても正しい計算方法があり、やり方を覚えなければいけません。そこで、どのように分数のかけ算をすればいいのか解説していきます。

1 分数と分数のかけ算の方法
- 1.1 整数と分数のかけ算では、整数を分数に直す
- 1.2 なぜ分数では分子同士と分母同士のかけ算をすることができるのか
2 帯分数のかけ算では、帯分数を仮分数に変える
3 約分できる場合の分数のかけ算
- 3.1 かけ算をする前に約分をして数字を小さくする
4 分数のかけ算ではかけ算の方法と約分が重要

分数と分数のかけ算の方法

まず、分数のかけ算の方法を学びましょう。分数のかけ算をするとき、やり方は簡単です。分母と分子について、それぞれかけ算しましょう。以下のようになります。

\(\displaystyle\frac{3}{4}×\displaystyle\frac{5}{2}=\displaystyle\frac{3×5}{4×2}=\displaystyle\frac{15}{8}\)

このように、分母同士のかけ算と分子同士のかけ算をします。たし算や引き算のように、分母を同じ数にそろえる必要はありません。そのためたし算や引き算とは異なり、分数のかけ算で通分をすることはありません。

分数のかけ算では分母同士、分子同士のかけ算をすればいいため、特に難しい計算方法ではありません。

整数と分数のかけ算では、整数を分数に直す

それでは、整数と分数はどのようにかけ算をすればいいのでしょうか。たとえば、以下のような計算になります。

\(2×\displaystyle\frac{2}{3}\)

この計算を理解するため、2を分数にしましょう。2を分数に変える場合、\(\displaystyle\frac{2}{1}\)とすることができます。整数は分数でもあるのです。ただ分母が1の場合、普通は分母を省きます。そのため整数では2と表記するものの、\(\displaystyle\frac{2}{1}\)と表記してもいいことを理解しましょう。

2を\(\displaystyle\frac{2}{1}\)に変えれば、分数のかけ算をすることができます。以下のようになります。

\(2×\displaystyle\frac{2}{3}=\displaystyle\frac{2}{1}×\displaystyle\frac{2}{3}=\displaystyle\frac{4}{3}\)

整数のままでは、どのように計算すればいいのか理解しにくいです。そこで整数を分数に変えれば計算のやり方が分かるようになります。

なぜ分数では分子同士と分母同士のかけ算をすることができるのか

それでは、なぜ分母をそろえることなく分数のかけ算をすることができるのでしょうか。これを理解するため、かけ算の性質を学びましょう。

分数のかけ算というのは、わり算とかけ算を同時にするのと意味が同じです。分数は以下のように、わり算に変えることができます。

\(\displaystyle\frac{4}{9}=4÷9\)
\(\displaystyle\frac{13}{2}=13÷2\)

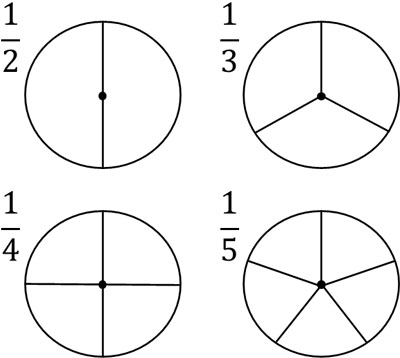
数字をわる場合、分母は大きくなります。何等分するのかを表すのが分母です。たとえば\(\displaystyle\frac{1}{2}\)は数字を2等分します。また、\(\displaystyle\frac{1}{3}\)は数字を3等分します。

そのため分数のかけ算をするとき、分母同士をかけることによって分母の数字が大きくなるのです。たとえば、\(\displaystyle\frac{1}{2}×\displaystyle\frac{1}{3}\)は分母同士のかけ算をして\(\displaystyle\frac{1}{6}\)になります。

また\(\displaystyle\frac{1}{2}×\displaystyle\frac{1}{3}\)とは、\(\displaystyle\frac{1}{2}\)を3等分することを意味します。図にすると、以下のようになります。

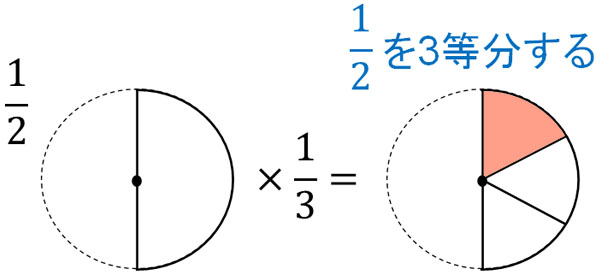
いくつに分割するのかを表すのが分母なので、分数のかけ算では分母同士をかけ算します。

また、分子は何個分かをあらわしています。たとえば\(\displaystyle\frac{2}{5}\)とは、\(\displaystyle\frac{1}{5}\)を2つ集めた数字です。また\(\displaystyle\frac{3}{5}\)とは、\(\displaystyle\frac{1}{5}\)を3つ集めた数字です。

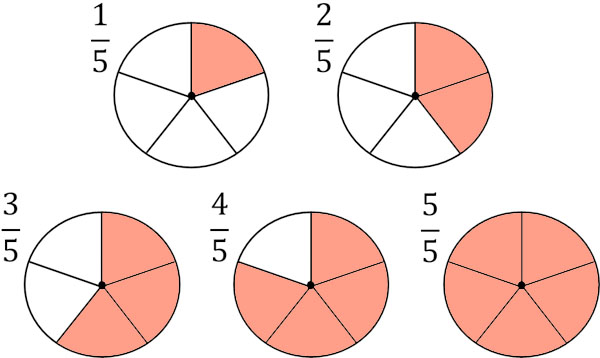
つまり分割したあと、いくつ集めるのかを表すのが分子です。

それでは、\(\displaystyle\frac{1}{2}×\displaystyle\frac{3}{4}\)はどのように考えればいいでしょうか。\(\displaystyle\frac{3}{4}\)をかけるため、\(\displaystyle\frac{1}{2}\)を4等分したあと、3つを集めましょう。以下のようになります。

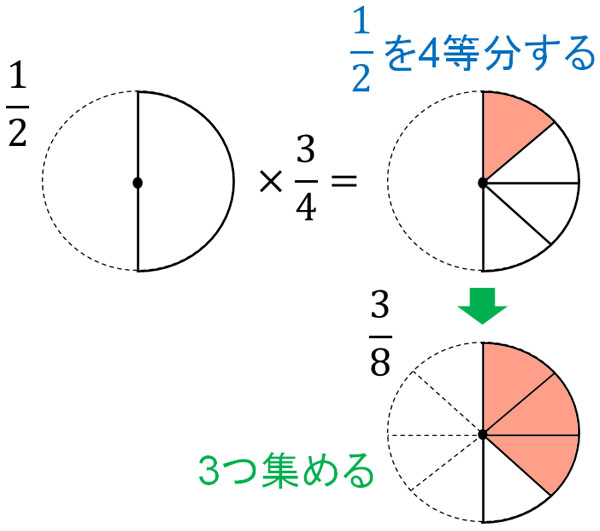
図を確認すると、\(\displaystyle\frac{1}{2}\)が4等分されるため、分母が8になっています。このように、分数のかけ算では分母同士をかけます。

また\(\displaystyle\frac{3}{4}\)の分子は3です。そのため、分割したあと3つ集めなければいけません。つまりを\(\displaystyle\frac{3}{4}\)かける場合、4等分をしたあと、3倍します。いいかえると、分子同士のかけ算をしていることになります。

そのため、以下の計算になります。

\(\displaystyle\frac{1}{2}×\displaystyle\frac{3}{4}＝\displaystyle\frac{1×3}{2×4}＝\displaystyle\frac{3}{8}\)

このように、分数のかけ算では分子同士・分母同士をかけることで答えを出します。

帯分数のかけ算では、帯分数を仮分数に変える

それに対して、帯分数のかけ算はどのようにすればいいのでしょうか。帯分数のたし算や引き算をする場合、帯分数のまま計算していいです。たとえば、以下のようになります。

\(1\displaystyle\frac{1}{4}+2\displaystyle\frac{2}{4}=3\displaystyle\frac{3}{4}\)

一方、帯分数のままかけ算をしてはいけません。帯分数のままかけ算をすると、間違った答えをだすことになります。たとえば、以下のかけ算はどのように計算すればいいでしょうか。

\(1\displaystyle\frac{1}{4}×1\displaystyle\frac{1}{2}\)

たし算のときと同じように、整数と分数をわけて計算すると間違います。2つの帯分数の整数部分を確認すると、両方とも1です。そのため、\(1×1=1\)です。また、分数同士をかけると\(\displaystyle\frac{1}{4}×\displaystyle\frac{1}{2}=\displaystyle\frac{1}{8}\)になります。そのため、\(1\displaystyle\frac{1}{4}×1\displaystyle\frac{1}{2}=1\displaystyle\frac{1}{8}\)が答えになると考える人は多いです。

しかし、この答えは間違っています。\(1\displaystyle\frac{1}{2}\)は1よりも大きい数字です。そのため\(1\displaystyle\frac{1}{2}\)をかけると答えが\(1\displaystyle\frac{1}{4}\)よりも大きくならなければいけません。先ほどの答えである\(1\displaystyle\frac{1}{8}\)は\(1\displaystyle\frac{1}{4}\)よりも小さい数字です。そのため、明らかに間違いであると分かります。

いずれにしても、帯分数のままかけ算をすると間違った答えがでてくると理解しましょう。

それでは、帯分数でのかけ算をするにはどうすればいいのでしょうか。以下の計算を考えてみましょう。

\(\displaystyle\frac{1}{4}×1\displaystyle\frac{1}{2}\)

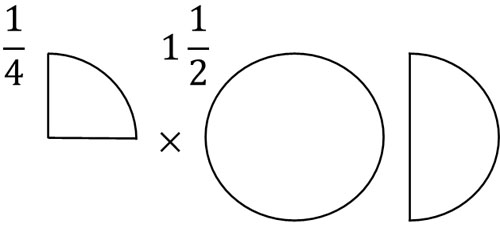
\(1\displaystyle\frac{1}{2}=1+\displaystyle\frac{1}{2}\)です。つまり、\(\displaystyle\frac{1}{4}×1\displaystyle\frac{1}{2}\)というのは、\(\displaystyle\frac{1}{4}\)が1つと\(\displaystyle\frac{1}{4}\)が\(\displaystyle\frac{1}{2}\)つあることを意味しています。そのため、以下のようになります。

\(\displaystyle\frac{1}{4}×1\displaystyle\frac{1}{2}\)

\(=\displaystyle\frac{1}{4}×1+\displaystyle\frac{1}{4}×\displaystyle\frac{1}{2}\)

\(=\displaystyle\frac{1}{4}+\displaystyle\frac{1}{8}\)

\(=\displaystyle\frac{2}{8}+\displaystyle\frac{1}{8}\)

\(=\displaystyle\frac{3}{8}\)

こうして、答えを出すことができました。

ただ、帯分数のまま計算をするのは非常にめんどうです。そこで、帯分数を仮分数に直しましょう。そうすれば、以下のように計算がかんたんになります。

\(\displaystyle\frac{1}{4}×1\displaystyle\frac{1}{2}=\displaystyle\frac{1}{4}×\color{red}{\displaystyle\frac{3}{2}}=\displaystyle\frac{3}{8}\)

仮分数（または真分数）であれば、分子同士・分母同士のかけ算をすることができます。ただ帯分数のかけ算では、必ず仮分数に直す必要があります。

約分できる場合の分数のかけ算

ここまで、約分をしない場合のかけ算について解説してきました。一方で約分できる場合、かけ算をするときに約分をしなければいけません。

分子と分母を同じ数でわったとしても、同じ答えになります。そこで、約分できる場合は必ず約分をしましょう。以下のようになります。

\(\displaystyle\frac{2}{3}×\displaystyle\frac{6}{3}=\displaystyle\frac{12}{9}=\displaystyle\frac{4}{3}\)

約分をしない場合、間違った答えになります。そのため分子と分母の公約数をみつけ、約分をしましょう。

かけ算をする前に約分をして数字を小さくする

なおかけ算をするとき、先に約分をするようにしましょう。つまり、答えをだした後に約分をするのではなく、かけ算をする前に約分をするのです。

さきにかけ算をする場合、以下のような計算になります。

\(\displaystyle\frac{3}{7}×\displaystyle\frac{14}{5}=\displaystyle\frac{42}{35}=\displaystyle\frac{6}{5}\)

42と35の最大公約数は7です。そこで分子と分母を7でわり、答えを出します。ただ大きい数字の公約数を探すのは大変です。そこで、かけ算をする前に約分をしましょう。

約分をするというのは、わり算をするのと意味が同じです。また同じ数字を利用する場合、かけ算をした後に割り算をするのと、わり算をしたあとにかけ算をするのでは、同じ答えになります。例えば、以下は同じ答えになります。

\(6\color{red}{÷2×4}=12\)
\(6\color{red}{×4÷2}=12\)

計算をするとき、通常は左から順に計算をしていきます。そうすると、\(÷2×4\)と\(×4÷2\)では順番が異なるものの、答えは同じになります。これは分数でも同じであり、かけ算をした後にわり算をするのではなく、わり算をした後にかけ算をしましょう。

そこで\(\displaystyle\frac{3}{7}×\displaystyle\frac{14}{5}\)について、分子と分母を確認しましょう。約分では分子と分母について、同じ数でわります。そこで分子と分母を確認し、同じ数でわれる場合、先にわり算をします。以下のようになります。

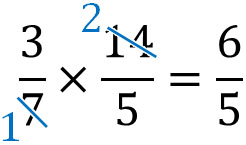
分子にある14と分母にある7をみると、公約数が7です。そこで、両方の数字をそれぞれ7でわりましょう。そうすると、このように\(\displaystyle\frac{3×14}{7×5}\)を\(\displaystyle\frac{3×2}{1×5}\)に変えることができます。そうすれば、分数のかけ算は非常にかんたんです。

分数のかけ算では、かけ算をする前に必ず約分をしましょう。これによって計算ミスを少なくすることができ、さらにはすばやく計算できるようになります。