数学では2つの方程式を利用して、計算問題を解くことがあります。式の中に分からない数字が2つある場合、答えを出すことはできません。ただ式が2つある場合、分からない数字が2つあったとしても答えを出すことができます。
2つ以上の方程式を組み合わせたものを連立方程式といいます。連立方程式を利用すれば、分からない答えが複数あったとしても答えを導き出せます。
連立方程式を解くには、2つのやり方があります。また中学数学は日常で利用するためのものであり、連立方程式では文章題を解けることが重要です。連立方程式の定義や解き方を学ぶだけでなく、あなた自身が式を作って問題を解けるからこそ意味があります。
そこで連立方程式の解き方だけでなく、どのように文章題で式を作ればいいのかについて解説していきます。
もくじ
連立方程式には2つの解き方がある
数学で学ぶ一次方程式は以下のような計算式です。
- \(2x+3y=8\)
ただ、この式だけでは答えが無限に存在します。\(x\)と\(y\)の値を自由に変えることができるからです。答えが8になる\(x\)と\(y\)のパターンはいくつもあります。
そこで、連立方程式では2つ以上の式を組み合わせます。例えば、以下のようになります。
\(\begin{eqnarray} \left\{\begin{array}{l}2x+3y=8\\2x+5y=12\end{array}\right.\end{eqnarray}\)
両方の式を満たす\(x\)と\(y\)は1つです。分からない数字が複数あったとしても、連立方程式を利用すれば明確な答えを出せるのです。重要なのは、連立方程式の解き方が2つあることです。以下の2つになります。
- 加減法
- 代入法
それぞれの方法について、解説していきます。
加減法は足し算・引き算によって\(x\)または\(y\)を消す
足し算または引き算によって、連立方程式の式を解く方法を加減法といいます。一次方程式の足し算または引き算をすることで、\(x\)または\(y\)のどちらか一方を消すのです。
例えば先ほどの連立方程式であれば、共通する文字として\(2x\)があります。そこで、引き算をすることによって以下のような一次方程式にすることができます。

係数が同じ場合、加減法によって文字を消すことができます。今回の計算では、方程式同士の引き算によって\(y=2\)と答えを出せます。
・代入して\(x\)または\(y\)の値を出す
その後、もう一方の答えも出しましょう。\(y=2\)と分かったため、次は\(x\)の値を出すのです。以下の式に対して、どちらか一方に\(y=2\)を代入します。
\(\begin{eqnarray} \left\{\begin{array}{l}2x+3y=8\\2x+5y=12\end{array}\right.\end{eqnarray}\)
どちらに\(y=2\)を代入してもいいです。両方とも、同じ答えになるからです。
- \(2x+3y=8\)の場合
\(2x+3×2=8\)
\(2x+6=8\)
\(2x=2\)
\(x=1\)
- \(2x+5y=12\)の場合
\(2x+5×2=12\)
\(2x+10=12\)
\(2x=2\)
\(x=1\)
2つの式を満たす\(x\)と\(y\)を出すのが連立方程式です。そのため当然ながら、どちらの式に代入しても最終的な答えは同じです。
プラスとマイナスで足し算・引き算を区別する
なお足し算をすればいいのか、それとも引き算をすればいいのかについては、符合を確認しましょう。係数の絶対値が同じであったとしても、符合がプラスなのかマイナスなのかによって計算方法が変わります。
先ほどの連立方程式では、係数の絶対値と符合が同じでした。そのため、引き算をしました。一方で係数の絶対値は同じであるものの、符合が違う場合はどうすればいいのでしょうか。例えば、以下のようなケースです。
\(\begin{eqnarray} \left\{\begin{array}{l}2x+2y=8\\4x-2y=10\end{array}\right.\end{eqnarray}\)
この場合、足し算をしましょう。以下のようになります。
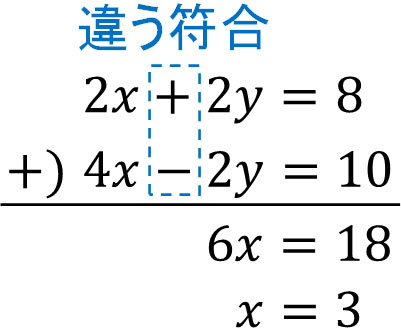
その後、\(x=3\)を代入することで\(y=1\)と答えを出すことができます。
加減法で足し算をするのか引き算をするのかについては、消したい文字がプラスなのかマイナスなのかによって区別するようにしましょう。
\(x\)または\(y\)の係数を揃える
先ほど、連立方程式で非常に簡単な例を用いて説明しました。ただ実際の計算では、それぞれの方程式の\(x\)や\(y\)の絶対値が異なることがよくあります。例えば、以下の連立方程式の答えは何でしょうか。
\(\begin{eqnarray} \left\{\begin{array}{l}2x+3y=16\\3x-4y=10\end{array}\right.\end{eqnarray}\)
\(x\)と\(y\)の両方とも、数字の絶対値は異なります。そこで、両辺の掛け算をすることで絶対値を合わせるようにしましょう。以下のようになります。

このように、文字の前にある数字の絶対値を揃えることができます。その後、方程式の足し算または引き算をすることによって、\(x\)と\(y\)の値を出すことができます。
\(x\)と\(y\)のうち、どちらの絶対値を揃えるのかはあなた次第です。計算しやすいように、係数の絶対値を合わせるようにしましょう。
・分数計算では、分数をなくすのが基本
なお、連立方程式では式の中に分数があるケースがよくあります。分数の足し算と引き算は難しく、計算ミスが頻繁に起こります。
そこで両辺の掛け算をすることで、分数をなくすようにしましょう。連立方程式で分数が式の中にある場合、分数をなくすことが答えを出すコツです。
代入法により、文字を消去する
なお連立方程式では、もう一つ解き方があります。それが代入法です。問題を解くとき、\(x\)や\(y\)に特定の数字を代入することで、答えを出したことがあるはずです。数学では、代入するのは数字だけでなく文字でも可能です。
そこで連立方程式では、代入することによって答えを出せます。例えば、以下の連立方程式を代入法によって解いていきましょう。
\(\begin{eqnarray} \left\{\begin{array}{l}x+3y=11\\2x-4y=-8\end{array}\right.\end{eqnarray}\)
代入法では、必ず\(x=☐\)または\(y=☐\)の式にします。さらに、文字の前の係数は必ず1でなければいけません。
先ほどの連立方程式では、\(x+3y=11\)の形を変えましょう。以下のように、\(3y\)を移項することで\(x=☐\)の形に変換することができます。
\(x+3y=11\)
\(x=-3y+11\)
方程式の形を変えることで、\(x=-3y+11\)となります。\(x\)は\(-3y+11\)であるため、これをもう一方の方程式である\(2x-4y=-8\)に代入しましょう。そうすると、加減法と同じように\(x\)を消すことができます。
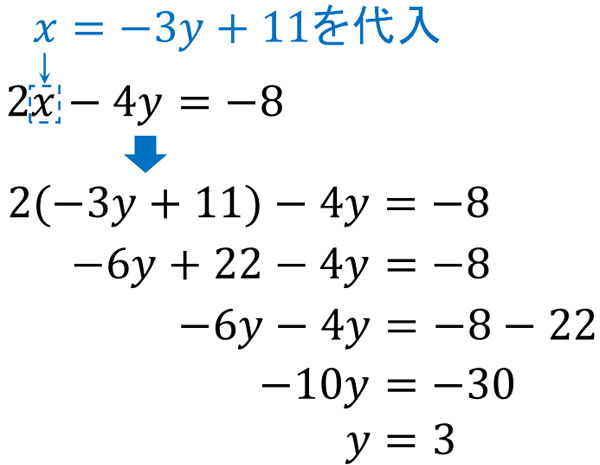
また\(y=3\)を式に代入することで、\(x=2\)と答えが出ます。
\(x=-3y+11\)
\(x=-3×3+11\)
\(x=2\)
代入法では、\(x\)または\(y\)の係数を1にしましょう。\(x=☐\)または\(y=☐\)の式を作った後、もう一方の方程式に代入することで答えを出すことができます。
加減法と代入法はどっちを使ってもいい
連立方程式を解くとき、加減法と代入法のどちらを使えばいいのか疑問に思う人がいます。これについては、どちらの方法を利用してもいいです。
問題によって、加減法を利用する方が簡単なことがあります。また、あるときは代入法を利用する方が簡単な計算になることがあります。数学ではできるだけ簡単な計算をするほど、計算ミスが少なくなります。そこで、加減法と代入法の両方の計算を行えるようにしましょう。
重要なのは、連立方程式では答えを出す方法が2つあるという事実です。
どちらの解き方が最適なのかについては、問題によって変わります。そこで、「計算が簡単になるほうはどちらか」を考えて連立方程式を解きましょう。
連立方程式の文章題の解き方
連立方程式の解き方を理解した後は、文章題の答えを出せるようにならなければいけません。
連立方程式を習う前は、必ず一次方程式を学びます。一次方程式でも、文章問題を解かなければいけません。数学で文章問題を解く方法は決まっており、問題文から式を作る必要があります。連立方程式でも、最初に式を作らなければいけません。
一次方程式では、分からない数字を\(x\)とします。一方で連立方程式では、分からない数字が2つあります。そこで、分からない数字をそれぞれ\(x\)と\(y\)にします。その後、連立方程式を作って答えを出します。全体の流れは以下のようになります。
- 分からない数字を\(x\)と\(y\)にする
- 2つの方程式を作る
- 連立方程式を解く
代数式では、必ず分からない数字をアルファベットにします。そこで、\(x\)と\(y\)を使って式を作りましょう。
連立方程式を利用した文章問題の例
それでは、実際に連立方程式の文章問題を解いてみましょう。
Q. 次の文章題を解きましょう
1個200円のオレンジと1個500円のスイカを合計で20個買い、合計金額は8200円でした。オレンジとスイカはそれぞれ、いくつ買いましたか。
A. 解答
連立方程式の文章題では、分からない数字を\(x\)と\(y\)にします。分からない数字としては、オレンジとスイカを買った数です。そこで、以下のようにします。
- オレンジを買った数:\(x\)
- スイカを買った数:\(y\)
そうすると、以下の2つの式を作ることができます。
\(\begin{eqnarray} \left\{\begin{array}{l}x+y=20\\200x+500y=8200\end{array}\right.\end{eqnarray}\)
オレンジとスイカの合計は20個です。そのため、\(x+y=20\)です。
また、オレンジの金額は\(200×x\)です。スイカの金額は\(500×y\)です。合計金額は8200円なので、\(200x+500y=8200\)とならなければいけません。そこで、この連立方程式を解きます。代入法を利用する場合、以下のようにします。
\(x+y=20\)
\(x=20-y\)
そこで、\(x=20-y\)を代入します。
\(200\color{red}{(20-y)}+500y=8200\)
\(4000-200y+500y=8200\)
\(300y=4200\)
\(y=14\)
また\(y=14\)を代入することで、\(x=6\)となります。そのためオレンジを6個、スイカを14個買ったと分かります。
必ず答えを代入して見直しをする
なお連立方程式では、答えを出した後に必ず見直しをするクセを付けましょう。見直しをすることが、問題を解くときに計算ミスを減らすコツになります。
例えば、以下の連立方程式を解くとします。
\(\begin{eqnarray} \left\{\begin{array}{l}4x+3y=14\\3x+2y=11\end{array}\right.\end{eqnarray}\)
例えば、この問題を解いて\(x=3,y=1\)となったとします。ただ、この答えは本当に正しいのでしょうか。一つの式だけでなく、両方の式に当てはめてみましょう。
- \(4x+3y=14\)の計算
\(4×3+3×1=15\) : 間違い
- \(3x+2y=11\)の計算
\(3×3+2×1=11\) : 正しい
このように、一つの方程式で答えが合いません。そのため、計算が間違っていると分かります。2つの方程式を満たすのが答えだからです。
そこで計算し直すと、\(x=5,y=-2\)となります。この場合、答えは両方の式を満たします。誰でも計算ミスをします。ただ、計算ミスは見直しによって防げるようになります。
練習問題:連立方程式の計算と文章題の解き方
Q1. 次の連立方程式を解きましょう
(a)
\(\begin{eqnarray} \left\{\begin{array}{l}0.4x+0.8y=6\\2x+1.2y=16\end{array}\right.\end{eqnarray}\)
(b)
\(\begin{eqnarray} \left\{\begin{array}{l}\displaystyle\frac{2}{3}x-\displaystyle\frac{3}{4}y=-5\\-\displaystyle\frac{1}{6}x+\displaystyle\frac{4}{2}y=23\end{array}\right.\end{eqnarray}\)
A1. 解答
分数が式の中に含まれる場合、両辺の掛け算によって分数をなくしましょう。同時に、絶対値を揃えるといいです。
(a)
\(\begin{eqnarray} \left\{\begin{array}{l}0.4x+0.8y=6\\2x+1.2y=16\end{array}\right.\end{eqnarray}\)
\(x\)と\(y\)を確認すると、\(x\)の係数を合わせる方が簡単そうに思えます。そこで、以下のようにします。
\(0.4x+0.8y=6\)
\((0.4x+0.8y)\color{red}{×5}=6\color{red}{×5}\)
\(2x+4y=30\)
そのため、以下の連立方程式に直すことができます。
\(\begin{eqnarray} \left\{\begin{array}{l}2x+4y=30\\2x+1.2y=16\end{array}\right.\end{eqnarray}\)
これを計算すると、以下のようになります。
\(\begin{array}{r}2x+4y=30\\\underline{-)\phantom{0}2x+1.2y=16}\\2.8y=14\end{array}\)
\(2.8y=14\)を計算すると、\(y=5\)となります。また連立方程式に\(y=5\)を代入することで、\(x=5\)となります。そのため、\(x=5,y=5\)が正解です。
(b)
\(\begin{eqnarray} \left\{\begin{array}{l}\displaystyle\frac{2}{3}x-\displaystyle\frac{3}{4}y=-5\\-\displaystyle\frac{1}{6}x+\displaystyle\frac{4}{2}y=23\end{array}\right.\end{eqnarray}\)
加減法でも代入法でも、問題を解くことができます。また、両辺の掛け算によって分数を消しましょう。以下の計算によって、それぞれの方程式の分数を消すことができます。
- \(\displaystyle\frac{2}{3}x-\displaystyle\frac{3}{4}y=-5\)
\(\left(\displaystyle\frac{2}{3}x-\displaystyle\frac{3}{4}y\right)\color{red}{×12}=-5\color{red}{×12}\)
\(8x-9y=-60\)
- \(-\displaystyle\frac{1}{6}x+\displaystyle\frac{4}{2}y=23\)
\(\left(-\displaystyle\frac{1}{6}x+\displaystyle\frac{4}{2}y\right)\color{red}{×(-6)}=23\color{red}{×(-6)}\)
\(x-12y=-138\)
\(x=12y-138\)
その後、\(x=12y-138\)を代入します。この例では、加減法ではなく代入法で問題を解きます。
\(8\color{red}{(12y-138)}-9y=-60\)
\(96y-1104-9y=-60\)
\(87y=1044\)
\(y=12\)
その後、\(y=12\)を代入して答えを出すと、\(x=6,y=12\)になります。
Q2. 次の文章題を解きましょう
家を出発して、2400m離れた図書館に向かいます。最初は分速100mで走ったものの、途中で疲れてしまい、分速40mで歩きました。図書館に到着するまで30分かかりました。走った時間と歩いた時間を求めましょう。
A3. 解答
走った時間を\(x\)分、歩いた時間を\(y\)分にします。走った時間と歩いた時間の合計は30分なので、以下の式が成り立ちます。
- \(x+y=30\)
また、走った距離は\(100×x\)です。それに対して、歩いた距離は\(40×y\)です。家から図書館まで2400mなので、以下の式が成り立ちます。
- \(100x+40y=2400\)
そこで、以下の連立方程式を解きます
\(\begin{eqnarray} \left\{\begin{array}{l}x+y=30\\100x+40y=2400\end{array}\right.\end{eqnarray}\)
加減法で解くと、以下のようになります。
\(x+y=30\)
\((x+y)\color{red}{×40}=30\color{red}{×40}\)
\(40x+40y=1200\)
\(\begin{array}{r}40x+40y=1200\\\underline{-)\phantom{0}100x+40y=2400}\\-60x=-1200\end{array}\)
\(-60x=-1200\)を計算すると、\(x=20\)になります。その後、\(x=20\)を代入することで\(y=10\)となります。そのため走った時間は20分、歩いた時間は10分です。
加減法と代入法によって連立方程式を解く
連立方程式を利用することで、分からない数字が2つあったとしても答えを出すことができます。この方法としては、加減法と代入法の2つがあります。連立方程式では、どちらも使います。そこで、最適な方法を選択するようにしましょう。
なお連立方程式では、分数の問題が出されることが頻繁にあります。分数があったとしても解き方は同じです。両辺に対して、掛け算をして係数を揃えましょう。
また数学で重要なのは、文章題を解けることがあります。式をあなたが作れるようになることで、日常生活で数学を応用できます。2つの式を作ることが文章題を解くときに重要です。
なお連立方程式では、必ず見直しをしましょう。あなたが出した答えを両方の式に代入することで、正しい答えになっているかどうか確認するのです。見直しまですることが、連立方程式の問題で正解を出すコツです。