中学数学で学ぶ内容として三平方の定理(ピタゴラスの定理)があります。長さの分からない辺があったとしても、三平方の定理を使うことで長さを計算できるようになります。
三平方の定理を理解するためには、平方根について既に学んでいる必要があります。ただ平方根を理解しているのであれば、三平方の定理を利用できます。
三平方の定理については、公式を暗記してしまいましょう。数学で頻繁に利用される公式が三平方の定理であり、公式を覚えていなければ計算問題を解くことができません。また特殊な三角形では、より簡単に辺の長さを出すこともできます。
そこでどのように三平方の定理を利用し、中学数学の計算問題を解けばいいのか解説していきます。
もくじ
三平方の定理の内容:直角三角形と辺の長さの関係
まず、三平方の定理とは何なのでしょうか。古代ギリシャの数学者、ピタゴラスが証明した公式が三平方の定理(ピタゴラスの定理)です。
三平方の定理では、必ず直角三角形を利用しなければいけません。直角三角形の場合、斜辺とその他の辺の関係は以下のようになります。
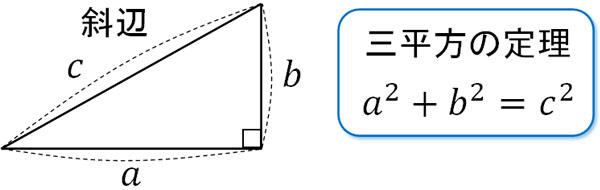
直角三角形の場合、すべての図形で三平方の定理が成立します。シンプルな公式なので、多くの計算で三平方の定理が利用されます。
分からない辺の長さを計算できる三平方の定理
なぜ三平方の定理が頻繁に利用されるのでしょうか。それは、分からない辺の長さを計算できるからです。
例えば、以下の辺\(a\)の長さはいくらでしょうか。
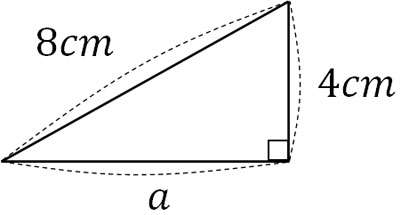
三平方の定理を利用すると、以下の式を作ることができます。
- \(8^2=a^2+4^2\)
この式を解くと、以下のようになります。
\(8^2=a^2+4^2\)
\(64=a^2+16\)
\(a^2=48\)
\(a=4\sqrt{3}\)
\(a^2=48\)の答えは\(±4\sqrt{3}\)の二つがあります。ただ図形の場合、答えがマイナスになることはありません。そのため、答えは\(a=4\sqrt{3}\)cmの一つだけです。
・斜辺やその他の辺の長さを計算できる
直角三角形で2つの辺の長さが分かれば、三平方の定理を利用して辺の長さを計算できます。斜辺やその他の辺の利用することによって、辺の長さを導き出すことができるのです。
なお、斜辺の場所を間違わないようにしましょう。以下が斜辺に該当します。
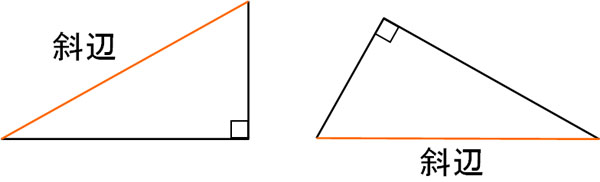
三平方の定理を利用する場合、必ず直角三角形でなければいけません。このとき、直角の向かい側にある辺が斜辺です。
ピタゴラスの定理が成り立つ証明
それでは、なぜピタゴラスの定理が成り立つのでしょうか。数学の問題を解くとき、三平方の定理を証明することはありません。ただ、公式が成立する理由を理解しておくのは知識として重要です。そこで、ピタゴラスの定理が成立する証明をしていきます。
まず、以下の三角形があるとします。
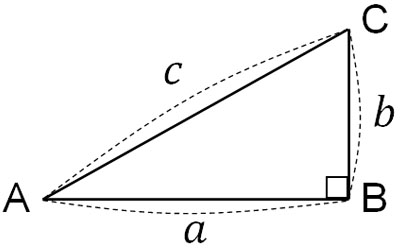
この三角形について、ACを辺とする正四角形を作ります。辺の長さは\(c\)であり、以下のようになります。
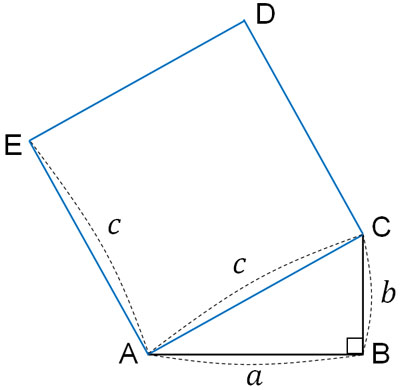
その後、正四角形ACDEの周辺に△ABCと合同の三角形を以下のように3つ配置します。
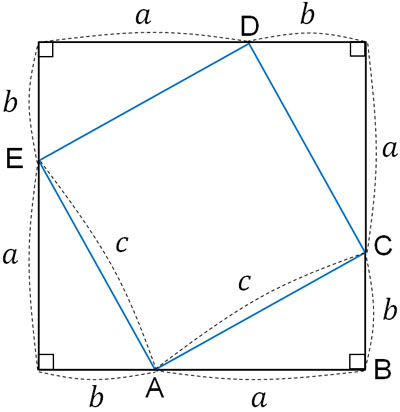
このとき、正方形ACDEの面積を出すためにはどのような計算式になるでしょうか。辺の長さは\(c\)なので、正方形ACDEの面積は\(c^2\)です。
また、正方形ACDEの面積は他の方法によって計算することができます。正方形ACDEの周辺に△ABCを配置することによって、大きい正方形を作りました。そこで大きい正方形の面積から、4つの△ABCを引けば、正方形ACDEの面積を出すことができます。
大きい正方形の面積は\((a+b)^2\)です。また、△ABCの面積は\(\displaystyle\frac{1}{2}ab\)です。そのため、正方形ACDEの面積は以下の式によって出すことができます。
- \((a+b)^2-\displaystyle\frac{1}{2}ab×4\)
そこで先ほどの正方形ACDEの面積\(c^2\)を利用することで、以下の式を作ることができます。
- \(c^2=(a+b)^2-\displaystyle\frac{1}{2}ab×4\)
この式を解くと、\(c^2=a^2+b^2\)になります。こうして、三平方の定理を証明することができました。
特殊な形の三角形で利用される三平方の定理
直角三角形であれば、すべての三角形で三平方の定理を利用できます。このとき中には、特殊な形の三角形があります。
特殊な形の三角形とはいっても、数学の問題では特殊な三角形と三平方の定理を利用して解かなければいけない問題が頻繁に出題されます。そこで三平方の定理の基本だけでなく、特殊な形の三角形を用いた三平方の定理を理解しましょう。
具体的には、以下の直角三角形が特殊な形に該当します。
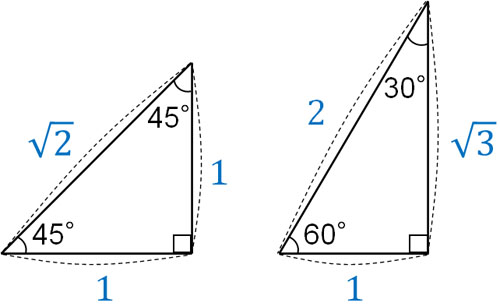
重要なのは、これらの直角三角形では辺の長さの比が決まっていることです。
角度が45°の直角三角形の場合、辺の比は\(1:1:\sqrt{2}\)になります。一方で角度が30°と60°の直角三角形では、辺の比は\(2:1:\sqrt{3}\)になります。
直角二等辺三角形:角度が45°の直角三角形
この辺の比は数学の計算で頻繁に利用されます。また辺の比を覚えていなければ、数学の問題を解くことができません。そのため、必ず辺の比を覚える必要があります。例えば、以下の辺\(a\)の長さはいくらでしょうか。
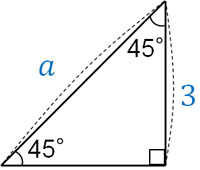
角度が45°の直角三角形の場合、上図で対応する辺の比は\(1:\sqrt{2}\)です。そのため、以下の比例式を作ることができます。
- \(1:\sqrt{2}=3:a\)
この式を解くと、\(a=3\sqrt{2}\)になります。辺の比を利用することによって、辺の長さを出すことができます。なお前述の通り、辺の比を覚えていなければ問題を解けないことに注意しましょう。
角度が30°と60°の直角三角形
一方で角度が30°と60°の直角三角形はどのように考えればいいのでしょうか。このときの考え方は先ほどと同じです。辺の比を利用することによって、辺の長さを計算しましょう。
例えば、以下の直角三角形で\(a\)の長さはいくらでしょうか。
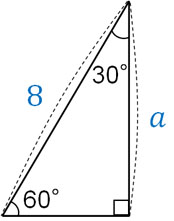
辺の比は\(2:1:\sqrt{3}\)です。このうち、上図に対応する辺の比は\(2:\sqrt{3}\)です。そのため、以下の比例式を作れます。
- \(2:\sqrt{3}=8:a\)
この式を解くと、\(a=4\sqrt{3}\)になります。\(2:\sqrt{3}\)のうち、どれが対応する辺なのか確認したうえで比例式を作りましょう。
立方体の対角線の長さを計算する:空間図形の計算
三平方の定理は平面図形で利用されるだけではありません。空間図形でも使われます。建築や構造力学で頻繁に三平方の定理が利用されるのは、空間図形で分からない辺の長さを計算することができるからです。
例えば、以下の直方体について、対角線の長さはいくらでしょうか。
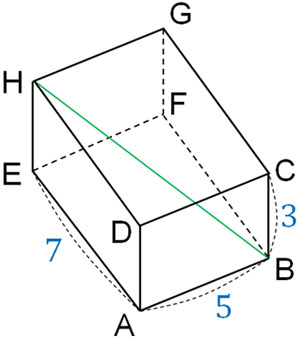
この計算をするためには、以下のように線を引きましょう。
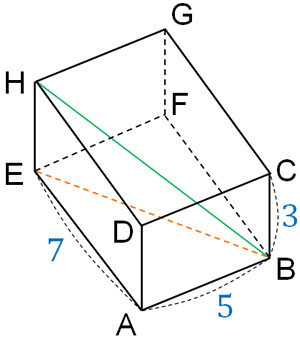
このとき、三平方の定理を利用することによって、EB2の数字を計算することができます。以下の通りです。
- \(EB^2=7^2+5^2=74\)
それでは、辺BHの長さはいくらでしょうか。△BEHは直角三角形なので、三平方の定理を使うことができます。またEB2の数字は分かっているため、以下のように辺BHの長さを計算できます。
- \(BH^2=74+3^2=83\)
- \(BH=\sqrt{83}\)
こうして、辺BHの長さは\(\sqrt{83}\)と計算することができました。
練習問題:ピタゴラスの定理を用いた計算
Q1. 以下の三角形について、辺ABを軸として1回転させたときにできる立体の体積を計算しましょう。
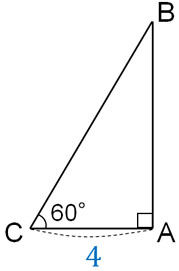
A1. 解答
まず、ABの長さを計算しましょう。ABが立体の高さになるからです。特殊な三角形の辺の比を利用することによって、以下の比例式を作ることができます。
- \(1:\sqrt{3}=4:AB\)
この計算を解くと、\(AB=4\sqrt{3}\)になります。ABを計算することができれば、あとは回転体の問題と同じです。ABを軸に一回転させる場合、以下の立体を作ることができます。
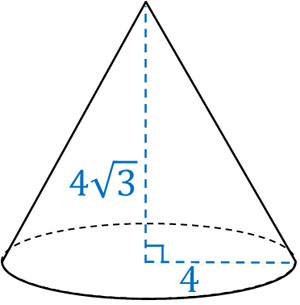
このような円錐になり、半径と高さが分かるので体積を計算することができます。
- \(4×4×π×4\sqrt{3}×\displaystyle\frac{1}{3}=\displaystyle\frac{64\sqrt{3}}{3}\)
こうして、円錐の体積は\(\displaystyle\frac{64\sqrt{3}}{3}\)と計算することができました。
分からない辺の長さを計算する
図形では、分からない長さの辺があったとしても計算することによって長さを導き出すことができます。直接、長さを測定しなくても計算できるのです。このとき頻繁に利用されるのが三平方の定理です。
直角三角形であれば、必ず三平方の定理を利用できます。2つの辺の長さが分かっている場合、残りの辺の長さを計算することができます。または特殊な形の直角三角形の場合、1つの辺の長さが分かれば、すべての辺の長さを計算できます。
ピタゴラスの定理を利用する場合、直角三角形を探すようにしましょう。その後、どれが斜辺なのかを確認し、計算問題を解くといいです。
ここでは、なぜ三平方の定理が成り立つのか証明しました。ただより重要なのは、三平方の定理を利用して問題を解けることだといえます。そこでピタゴラスの定理を利用して、平面図形や空間図形の辺の長さを計算できるようにしましょう。






