平方根の計算では分数が頻繁に出てきます。分数の計算では、分母にルートが含まれることがあります。その場合、分母に根号(ルート)があるままでは不正解です。
根号の計算問題では、分母にルートが含まれる場合、分母の根号を消すようにしましょう。この作業を分母の有理化といいます。平方根の分数では、分子にルートが含まれるのは問題ないが、分母にルートが含まれると微妙です。
それでは、どのようにして分母の有理化をすればいいのでしょうか。また、なぜ分母の有理化をする必要があるのでしょうか。
これらを学ぶことにより、数学で分母の有理化を正しく行う手順を理解できるようになります。どのように分母の有理化をするのかについて、やり方を解説します。
もくじ
分母にルートがある場合、有理化をする
平方根の分数では、分母にルートが表れることがあります。例えば、以下のような状態がこれに該当します。
- \(\displaystyle\frac{1}{\sqrt{2}}\)
この分数では、分母に\(\sqrt{2}\)が含まれています。そこで、分母にルートのない分数にしましょう。

ルートは無理数です。数学では、分母に無理数が含まれている状態は好ましくありません。そこで、分母の数を無理数ではなく、有理数の数字に変えます。分母に存在するルートを分子に移動させるのです。これが分母の有理化です。
中学数学では、分母にルートが残っていると不正解になります。そこで、分母の有理化を必ず行うようにしましょう。
分母の根号を整数にする手順
どのようにして分母の有理化をすればいいのでしょうか。方法としては、分母と分子に同じ数を掛けるようにしましょう。分数では、分子と分母に対して同じ数の掛け算または割り算をしても問題ありません。事実、以下の分数はすべて同じ数字です。
- \(\displaystyle\frac{1}{2}=\displaystyle\frac{2}{4}=\displaystyle\frac{3}{6}\)
また、\(\displaystyle\frac{1}{2}=\displaystyle\frac{1×2}{2×2}\)と考えることもできます。いずれにしても、分数では同じ数字を分子と分母に対して掛けることができます。
この性質を利用して、分母の有理化をしましょう。ルートを2乗すると、根号が外れます。そこで、分母にあるルートと同じ数字を分子と分母に掛けます。以下のようになります。
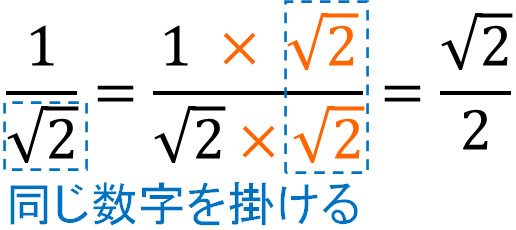
\((\sqrt{2})^2=2\)であり、同じ数のルートの掛け算によって分母の数を整数に変換できます。分母の有理化のやり方は難しくありません。分母にある平方根の掛け算をするだけです。
ルート内の数字を小さくすると計算ミスが少ない
なお分母の有理化をするとき、ルート内の数字を小さくすると計算ミスが少なくなります。最初に素因数分解をすることで、数字を小さくするのです。
例えば、以下の分数はどのように有理化すればいいのでしょうか。
- \(\displaystyle\frac{\sqrt{63}}{\sqrt{72}}\)
分母の有理化をするとき、2つのやり方があります。一つは、最初にルート内の数字を小さくする方法です。もう一つは、最初に素因数分解をせずに分母の有理化をする方法です。2つの方法を比べてみると、以下のようになります。
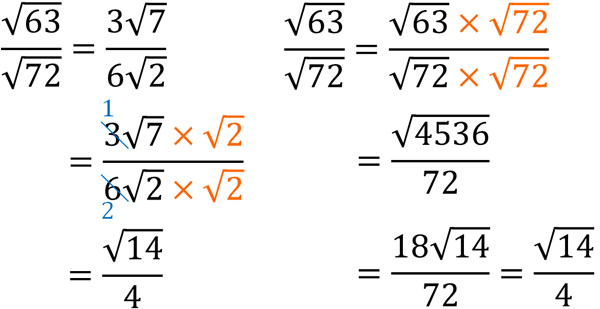
このように比較すると、最初に素因数分解をすることで、根号の中にある数字を小さくしたほうが計算は簡単です。つまり、計算ミスが少なくなります。
どのような人であっても、数学の計算でミスをします。そこで、ミスをできるだけ少なくする方法を選択しなければいけません。分母の有理化をするにしても、最初に素因数分解をすると計算ミスが少なくなります。
分母に項が2つある足し算・引き算の有理化
なお分母の有理化を行うときの応用問題として、分母に2つの項があるケースがあります。ルートが一つだけでなく、足し算または引き算が含まれているのです。
例えば、以下の分数では分母に項が2つ含まれています。
- \(\displaystyle\frac{1}{3-\sqrt{2}}\)
この場合、どのように計算すればいいのでしょうか。2つの項がある場合、乗法公式を利用します。具体的には、以下の公式を使いましょう。
- \((x+a)(x-a)=x^2-a^2\)
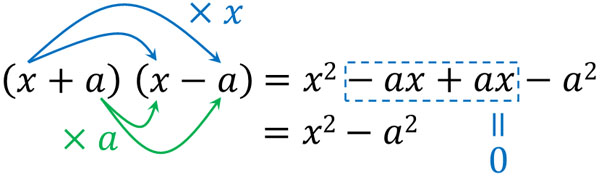
この公式を利用することで、分母の有理化が可能です。例えば先ほどの計算式であれば、以下のように計算できます。
\(\displaystyle\frac{1}{3-\sqrt{2}}\)
\(=\displaystyle\frac{1\color{red}{×(3+\sqrt{2})}}{(3-\sqrt{2})\color{red}{×(3+\sqrt{2})}}\)
\(=\displaystyle\frac{3+\sqrt{2}}{3^2-(\sqrt{2})^2}\)
\(=\displaystyle\frac{3+\sqrt{2}}{9-2}\)
\(=\displaystyle\frac{3+\sqrt{2}}{7}\)
このように、乗法公式を利用することで分母の有理化が可能です。項が2つあったとしても、以下の方法によって分母の有理化をすることができます。
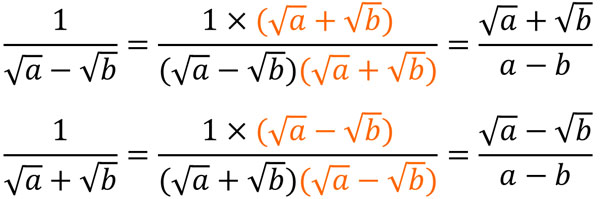
分母にルートの足し算や引き算が含まれていることがあります。その場合、乗法公式を利用して分母の有理化をしましょう。
分数でなぜ分母の有理化が必要なのか
それでは、なぜ平方根の分数では分母の有理化が必要なのでしょうか。分母にルートがあると、何が問題なのでしょうか。
分母の有理化をしないといけない理由として、数字を分かりやすくすることがあります。例えば、以下の分数ではどのような数字なのか理解しにくいです。
- \(\displaystyle\frac{1}{\sqrt{2}}\)
無理数は数字が永久に続きます。そのような数字で分子を割るのは不可能であり、どのような数字になるのか想像しにくいです。
一方で分母の有理化を行い、分数を以下の形に変えればどうでしょうか。
- \(\displaystyle\frac{\sqrt{2}}{2}\)
無理数なので、分子にある数字が永久に続くのは同じです。ただ、どのような数字になるのか容易に想像できます。\(\sqrt{2}≒1.41\)です。そのため、\(\displaystyle\frac{\sqrt{2}}{2}\)は約0.7と分かります。
分母に無理数があると、数字が分かりにくいです。一方でルートがあったとしても、分子であればどのような数字なのか理解しやすいです。
通分をする場合、分母の有理化が必要
また通分をするときについても、分母を有理化しているほうが好ましいです。分数の足し算と引き算では、必ず分母が揃っていなければいけません。分母が揃うことで、分数の性質が同じになるからです。
ただ分母が無理数を含んでいると、分母を揃えるのが困難です。例えば、以下の計算はどのようにすればいいでしょうか。
- \(\displaystyle\frac{1}{3}+\displaystyle\frac{1}{2+\sqrt{2}}\)
この状態では、計算が困難です。分母に無理数があるため、数字を揃えることができません。そこで、分母の有理化をしましょう。そうすれば、通分できるようになります。
\(\displaystyle\frac{1}{3}+\displaystyle\frac{1}{2+\sqrt{2}}\)
\(=\displaystyle\frac{1}{3}+\displaystyle\frac{1\color{red}{×(2-\sqrt{2})}}{(2+\sqrt{2})\color{red}{×(2-\sqrt{2})}}\)
\(=\displaystyle\frac{1}{3}+\displaystyle\frac{2-\sqrt{2}}{4-2}\)
\(=\displaystyle\frac{1}{3}+\displaystyle\frac{2-\sqrt{2}}{2}\)
\(=\displaystyle\frac{2}{6}+\displaystyle\frac{(2-\sqrt{2})×3}{6}\)
\(=\displaystyle\frac{2}{6}+\displaystyle\frac{6-3\sqrt{2}}{6}\)
\(=\displaystyle\frac{8-3\sqrt{2}}{6}\)
分母を整数にするからこそ、分数の通分が可能になります。無理数が分母にあると、通分できません。分母の有理化が必要な理由としては、通分することで分数同士を計算できるようにする必要があるからです。分母の有理化をしないと、計算できないのです。
練習問題:分母の有理化の計算
Q1. 分母の有理化をしましょう
- \(\displaystyle\frac{4}{\sqrt{8}}\)
- \(\displaystyle\frac{\sqrt{3}}{\sqrt{24}}\)
- \(\displaystyle\frac{1}{\sqrt{6}+\sqrt{3}}\)
A1. 解答
これまで説明してきたことを理解すれば、どの問題も簡単に解くことができます。
(a)
\(\displaystyle\frac{4}{\sqrt{8}}\)
\(=\displaystyle\frac{4}{2\sqrt{2}}\)
\(=\displaystyle\frac{2}{\sqrt{2}}\)
\(=\displaystyle\frac{2\color{red}{×\sqrt{2}}}{\sqrt{2}\color{red}{×\sqrt{2}}}\)
\(=\displaystyle\frac{2\sqrt{2}}{2}\)
\(=\sqrt{2}\)
(b)
\(\displaystyle\frac{\sqrt{3}}{\sqrt{24}}\)
\(=\displaystyle\frac{\sqrt{3}}{2\sqrt{6}}\)
\(=\displaystyle\frac{\sqrt{3}\color{red}{×\sqrt{6}}}{2\sqrt{6}\color{red}{×\sqrt{6}}}\)
\(=\displaystyle\frac{\sqrt{18}}{2×6}\)
\(=\displaystyle\frac{3\sqrt{2}}{12}\)
\(=\displaystyle\frac{\sqrt{2}}{4}\)
(c)
\(\displaystyle\frac{1}{\sqrt{6}+\sqrt{3}}\)
\(=\displaystyle\frac{1\color{red}{×(\sqrt{6}-\sqrt{3})}}{(\sqrt{6}+\sqrt{3})\color{red}{×(\sqrt{6}-\sqrt{3})}}\)
\(=\displaystyle\frac{\sqrt{6}-\sqrt{3}}{(\sqrt{6})^2-(\sqrt{3})^2}\)
\(=\displaystyle\frac{\sqrt{6}-\sqrt{3}}{3}\)
平方根では分母にある根号を消す
数学で平方根を取り扱うとき、必ず行わなければいけない計算があります。その一つが分母の有理化です。分母に根号が含まれている場合、そのままの状態では間違いです。必ず分母の有理化をするようにしましょう。
分母の有理化をするからこそ、どのような数字なのか計算しやすくなります。また分数の通分が可能になり、足し算や引き算が可能になります。なぜ、分母の有理化が必要なのかまで含めて理解しましょう。
なお、分母の有理化を行うやり方は簡単です。分母にあるルートと同じ数を分子と分母に掛けましょう。このとき、先に素因数分解によって根号の中の数字を小さくしておくと計算ミスが減ります。また、分母に項が2つある場合は乗法公式を利用しましょう。
分母の有理化では正しいやり方があります。分母の有理化をする方法を理解して、平方根の計算をするようにしましょう。