中学数学の二次関数：問題の解き方の基本とグラフの書き方

中学数学では二次関数を学びます。二乗のグラフが二次関数であり、グラフにはカーブがあります。

グラフを含む数学では、中学生では最初に比例を学びます。比例を応用させたグラフが一次関数です。一次関数のさらなる発展問題が二次関数です。一次関数と二次関数は考え方がほぼ同じであり、違いは$x^2$が式の中にあるかどうかだけです。

ただ二次関数では、グラフの形が大きく異なります。また覚えなければいけない二次関数の特徴も存在します。

さらに二次関数の問題では、一次関数と組み合わせることがよくあります。そこで、どのようにして二次関数の問題を解けばいいのか解説していきます。

$y=ax^2$の方程式が二次関数

$x$に数字を代入したとき、$y$の値が明確に決定される方程式が関数です。一次関数では、例えば以下の式になります。

• $y=x+2$

このような式では、$x$が2倍になると、$y$の増加量も2倍になります。そのため、$y$と$x$の値は比例の関係にあります。

一方で二次関数では、例えば以下のような式になります。

• $y=x^2$

この場合、$x$の値が2倍になると、$y$の値は2²倍（4倍）になることが分かります。つまり、$y$の値は$x^2$に比例しているといえます。$x$の値が増えると、$y$の値は二乗の掛け算によって増えていきます。

二次関数の式では、例えば以下のようなものがあります。

• $y=5x^2$
• $y=-3x^2$
• $y=x^2$
• $y=\displaystyle\frac{1}{2}x^2$

このように、式によって$x^2$の前にある数字が変わります。そのため二次関数は以下の公式によって表されます。

• $y=ax^2$

二次関数で最も基本的な式が$y=ax^2$で表される方程式です。

世の中の自然現象の多くが二次関数

なぜ、二次関数を学ぶ必要があるのでしょうか。それは、私たちの身の回りにある多くの現象が二次関数になっているからです。

例えば斜面にボールを置いて離すとき、ボールの速度はどのようになるでしょうか。ボールから手を離した直後、ボールのスピードは遅いです。ただ、時間経過と共にボールの速度は徐々に早くなります。常に一定の速度となる比例ではなく、時間経過と共に速度が速くなる二次関数になるのです。

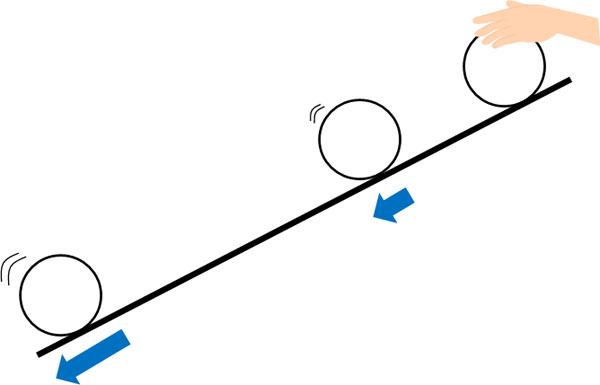
他にも、止まっている車がスピードを上げるとき、二次関数にて速度が上昇します。もちろん車に限らず、ロケットを打ち上げるときのスピードを計算するとき、二次関数を利用します。あらゆる場面で二次関数が利用されていることを理解しましょう。

二次関数の表は$x^2$に比例する

それでは、二次関数はどのような表になるのでしょうか。比例とは異なり、前述の通り二次関数は$x^2$に比例します。

例えば$y=x^2$の式では、以下のような表になります。

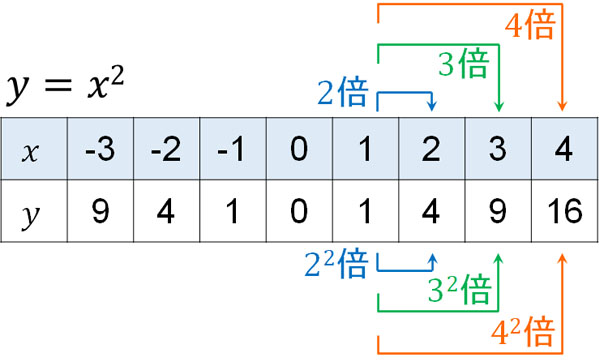
$x$が2倍になれば、$y$は4倍になります。$x$が3倍になれば、$y$は9倍になります。$x$が4倍になれば、$y$は16倍になります。

$y=x^2$の式になっているため、$x$の値が増えると、$y$の値は$x$の二乗になります。重要なのは、$y$の値が2乗で増えていく式であることです。

二次関数は放物線のグラフになる

それでは、二次関数の式をグラフに書くとどのようになるのでしょうか。例えば$y=x^2$のグラフは以下のようになります。

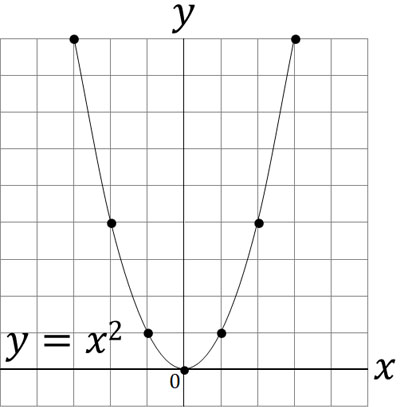
このように、曲線のグラフになります。グラフの書き方としては、$x$と$y$の座標をグラフ上に記入します。その後、座標をなめらかな曲線で結ぶことで二次関数のグラフを書けるようになります。

$y=ax^2$のグラフは必ず原点を通ります。$(0,0)$の座標を通るのが、$y=ax^2$のグラフによる二次関数です。

なお、二次関数のグラフの曲線はボールを投げたときに描く軌道と同じです。事実、物を空中に投げるとき、スピードは二次関数で計算できます。

先ほど、ロケットの軌道は二次関数で計算すると解説しました。この理由としては、ロケットは空中を飛ぶからです。また大昔であれば、大砲を飛ばすときの軌道を計算するときに二次関数を利用していました。二次関数は科学技術や戦争を含め、あらゆる場面で応用されています。

二次方程式のグラフの線は放物線といいます。空中にある物体はどれも放物線を描くようになり、二次関数と同じ曲線になります。

$a$の値でグラフの形が変わる

なお$y=ax^2$のグラフを書くとき、グラフの形は$a$の値によって変わると考えましょう。$a$の絶対値が大きくなるほど、グラフは急になります。一方で$a$の絶対値が小さくなるほど、グラフはゆるやかになります。

以下のように、$a$の値によってグラフの形が変わります。

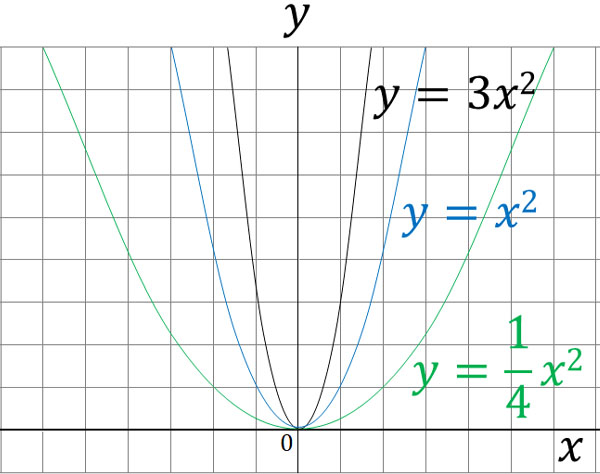
グラフが原点$(0,0)$を通るのは同じです。また放物線の曲線になるのも共通しています。違うのは、$a$の値によってグラフの形が変わることです。

$a>0$で下に凸になり、$a<0$で上に凸になる

また、他に重要なポイントがあります。それは、$a$の値が正の数なのか、それとも負の数なのかによってグラフの向きが変わることです。

二次関数のグラフでは、$a$が正の数（$a>0$）だと下に凸になります。一方で$a$が負の数（$a<0$）だと、上に凸になります。具体的には、以下のようになります。

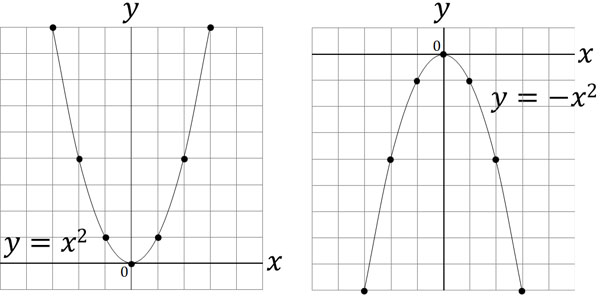
二次関数では$x$の値を二乗します。そのため$x$の値がプラスでもマイナスでも、必ず答えはプラスになります。

ただ二次関数では、$a$の値を掛けます。そのため$a$の値が正の数だと、$x$の値が大きくなるほど$y$の値も大きくなります。一方で$a$の値が負の数だと、$x$の値が大きくなるほど$y$の値は小さくなります。

二次関数での変化の割合は異なる

なお二次関数では、変化の割合を求めなければいけないことがあります。一次関数の計算をするとき、変化の割合は非常に重要です。「変化の割合＝傾き」だからです。変化の割合を計算することで、傾き$a$を出すことができます。

ただ一次関数と二次関数では、変化の割合に対する考え方が異なります。一次関数では、変化の割合は常に一定です。一方で二次関数では、変化の割合が場所によって変化します。

変化の割合を計算するとき、以下の公式があります。

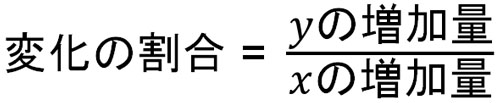
一次関数ではこの公式を覚えなくてもいいです。前述の通り、変化の割合と傾きは意味が同じだからです。一方で二次関数ではどうなのでしょうか。二次関数でも、変化の割合の公式を覚える意味はありません。

変化の割合とは、要は「$x$の値が1増えたとき、$y$の値がいくら増えるのか」を指します。この定義を理解していれば、変化の割合の公式を覚える必要はありません。比の性質を使えばいいからです。以下のようになります。

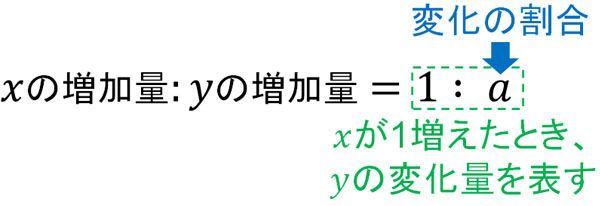
比の性質を利用すれば、変化の割合を出すことができます。例えば、以下のようになります。

• $x$の値が1増えたとき、$y$の値が2増えている：変化の割合は2
• $x$の値が1増えたとき、$y$の値が-4増えている：変化の割合は-4
• $x$の値が7増えたとき、$y$の値が3増えている：変化の割合は$\displaystyle\frac{3}{7}$

例えば$x$の値が7増えたとき、$y$の値が3増えている場合、比は$7:3=1:a$です。これを解くと、$a=\displaystyle\frac{3}{7}$です。利用頻度が低く、そこまで重要でない公式を覚えても確実に忘れます。そうではなく、「なぜそうなるのか」の原理原則を理解して、公式なしに値を出さなければいけません。

数学では、公式を覚えなければいけない場面とそうでない場面があります。変化の割合については、公式を覚える意味はありません。

・二次方程式の変化の割合

なお前述の通り、二次関数では座標によって変化の割合が変わります。どのように二次関数での変化の割合を考えればいのでしょうか。例として、$y=x^2$のグラフで以下のとき、変化の割合を計算してみましょう。

• $x$の値が1から2へ変化するとき
• $x$の値が-3から-1へ変化するとき

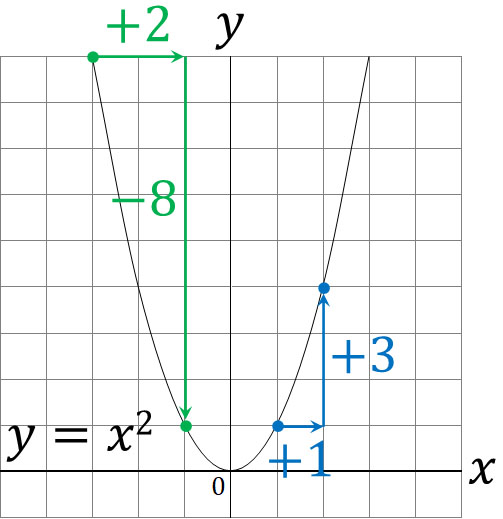
$x$の値が1から2へ変化するとき、$y$の値は3増えます。$x$が1増えると、$y$は3増えるため、変化の割合は3です。

一方で$x$の値が-3から-1へ変化するとき、$y$の値は-8増えます。$x$が2増えると、$y$は-8増えます。$2:-8=1:a$の比になるため、変化の割合は-4です。

2点を通る一次関数を求める

それでは、二次関数でなぜ変化の割合を求める必要があるのでしょうか。それは、以下のように二次関数と一次関数を組み合わせた問題を解かなければいけないからです。

二次関数の変化の割合は変わるものの、一次関数の変化の割合は変わりません。そのため二次関数について、2点の座標を結ぶ直線については、変化の割合は常に一定です。傾きが変化の割合だからです。

二次関数で変化の割合を求めるというのは、「2つの座標を結ぶ直線の傾きを出す」のと意味が同じです。参考までに、先ほどのグラフでは$(-1,1)$と$(3,9)$が交点です。つまり$x$が4増えた結果、$y$は8増えています。

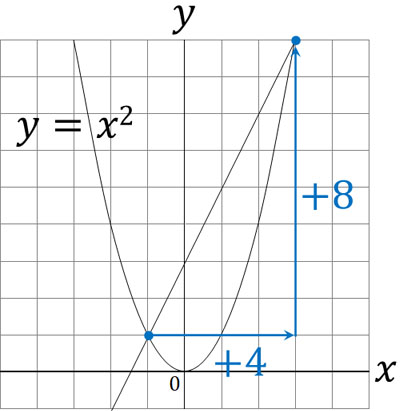
「$x$の増加量：$y$の増加量＝1：$a$」に当てはめると、$4:8=1:a$になります。これを解くと、$a=2$となります。

また2点の座標を通る直線を確認すると、$(0,3)$の座標を通っていることが分かります。つまり、切片は3です。そのため、2点の交点を通る直線の一次関数は以下になります。

• $y=2x+3$

こうして、二次関数の2つの座標を結ぶ直線について、一次関数を導き出すことができます。二次関数の発展問題として、こうした数学の計算問題が頻繁に出されるため、解けるようにしておきましょう。

練習問題：二次関数のグラフの問題

Q1. 次の問題を解きましょう

$y=ax^2$のグラフ(1)と$y=ax+b$のグラフ(2)があります。原点をO、(1)と(2)の交点をA、Bとします。Aの$x$座標は-2、Bの$x$座標は6です。また、(2)の直線と$x$座標との交点をCとします。

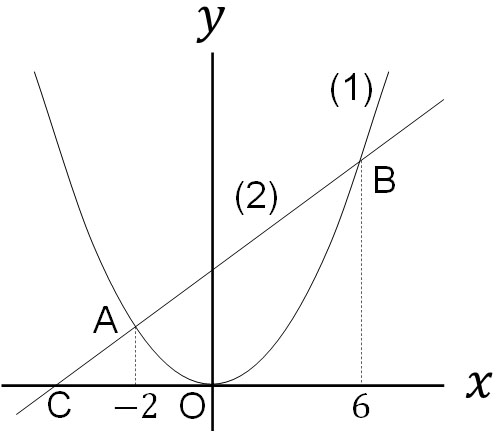
1. (1)のグラフについて、$x$の値が-6から-2に増加したとき、$y$の値は-16増えました。$a$の値を求めましょう
2. (2)の直線の式を求めましょう
3. △AOBの面積を求めましょう
4. (1)のグラフ上に点Dを取ります。△CODの面積が27となるとき、点Dの$x$座標を求めましょう

A1. 解答

二次関数の問題では、二次関数に関する問題だけが出されるとは限りません。この問題のように、二次関数と関連させた一次関数や連立方程式、図形など多くの問題の複合問題となるのは普通です。

(a)

変化の割合から二次関数の式を出すためにはどうすればいいのでしょうか。これについて、$x$と$y$の増加量を考えてみましょう。

$x$の値が-6から-2に増加したとき、$x$の値は4増えています。このとき、$y$の値はいくら増えているでしょうか。$y=ax^2$の式に代入してみましょう。

$x$の値が-6のとき、$y=a×(-6)^2=36a$です。$x$の値が-2のとき、$y=a×(-2)^2=4a$です。36aから4aになっているため、$y$は-32a増えています。

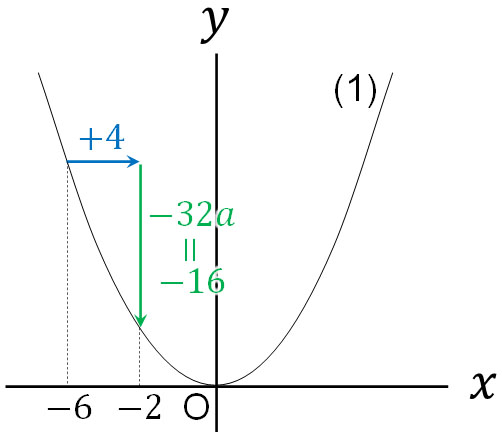
$y$の変化量は-16と既に分かっているため、以下のように計算できます。

$-32a=-16$

$a=\displaystyle\frac{-16}{-32}$

$a=\displaystyle\frac{1}{2}$

こうして、(1)の関数は$y=\displaystyle\frac{1}{2}x^2$と分かります。

(b)

$y=\displaystyle\frac{1}{2}x^2$なので、AとBの座標が分かります。$x$の値を代入することで、それぞれ以下の座標になると分かります。

• A$(-2,2)$
• B$(6,18)$

2つの座標が分かっている場合、連立方程式によって一次方程式を解くことができます。つまり、(2)の式が分かります。$y=ax+b$に代入することで、以下の連立方程式を解くのです。

$\begin{eqnarray} \left\{\begin{array}{l}2=–2a+b\\18=6a+b\end{array}\right.\end{eqnarray}$

この連立方程式を解くことによって、一次関数の式を出せます。

ただ、もう一つの方法によって(2)の式を出すことも可能です。それは、変化の割合を使う方法です。二次関数で変化の割合について学んだため、この問題では変化の割合を利用して(2)の式を出してみましょう。

点Aと点Bを比べたとき、変化の割合はいくらでしょうか。A$(-2,2)$からB$(6,18)$に移動するとき、$x$の値は8増え、$y$の値は16増えています。変化の割合は$x$の値が1増えるとき、$y$の値がいくら増えるのかを表します。そのため、以下の比になります。

• $8:16=1:a$

比の性質を利用すると以下のように計算できます。

$16=8a$

$a=2$

こうして、(2)の一次関数の傾き（変化の割合）は2と分かります。そのため、一次関数の式は$y=2x+b$です。

その後、A$(-2,2)$またはB$(6,18)$を代入することで切片を出しましょう。例えば、$(6,18)$を代入すると以下のようになります。

$18=2×6+b$

$18=12+b$

$b=6$

こうして、(2)の一次関数は$y=2x+6$と分かります。

(c)

△AOBの面積はどのように計算すればいいのでしょうか。(2)の切片（$y$座標との交点）をPとすると、以下のようになることが分かります。

• $△AOB=△AOP+△BOP$

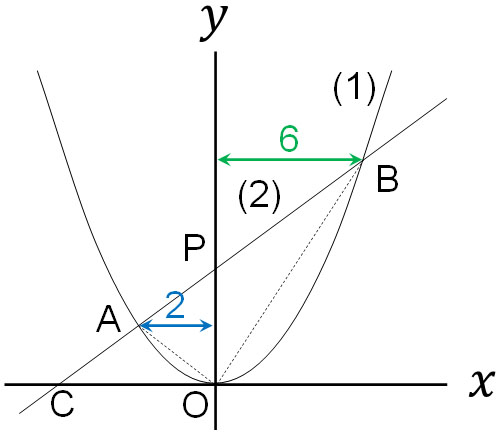
そこで、△AOPと△BOPの面積を求めましょう。(2)の式は$y=2x+6$なので、Pの座標は$(0,6)$です。つまり、三角形のたて（線分PO）の長さは6です。

一方でAの$x$座標は-2なので、△AOPの横の長さは2です。Bの$x$座標は6なので、△BOPの横の長さは6です。そのため、以下のようにそれぞれの面積を出せます。

• △AOPの面積：$6×2×\displaystyle\frac{1}{2}=6$
• △BOPの面積：$6×6×\displaystyle\frac{1}{2}=18$

それぞれの三角形の面積を足すと、以下のように答えがでます。

• $△AOB=6+18=24$

(d)

(1)の上に点Dがある場合、△CODは以下のようになります。

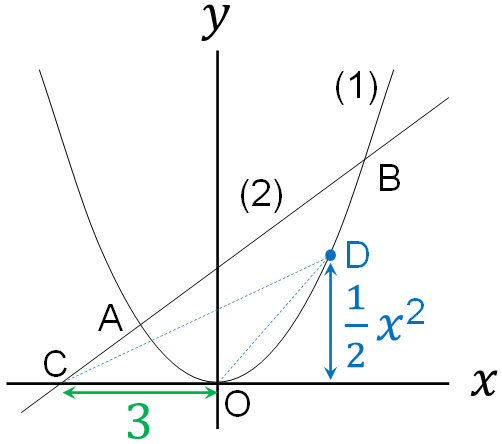
(2)の一次関数は$y=2x+6$です。そのため、$x$軸との交点は$y=0$を代入することで以下のように計算できます。

$0=2x+6$

$-2x=6$

$x=-3$

点Cの座標は$(-3,0)$です。つまり、COの長さは3です。一方で△CODのたての長さはいくらでしょうか。(1)の二次関数は$y=\displaystyle\frac{1}{2}x^2$です。そのため点Dの座標は$(x,\displaystyle\frac{1}{2}x^2)$です。つまり、たての長さは$\displaystyle\frac{1}{2}x^2$です。

△CODの面積は27です。三角形の面積の公式に当てはめると、以下のように計算できます。

$3×\displaystyle\frac{1}{2}x^2×\displaystyle\frac{1}{2}=27$

$x^2=27×\displaystyle\frac{4}{3}$

$x^2=36$

$x=-6,x=6$

こうして$x=-6$または$x=6$のとき、△CODの面積が27になります。

二次関数のグラフを読み、方程式を解く

中学数学で学ぶ二次関数は一次関数と性質が似ています。ただ、覚えることはそれなりに多く、放物線の概念を理解しなければいけません。

また二次関数の問題を解く場合、二次関数に関することだけを問われるとは限りません。一次方程式や連立方程式、一次関数、図形を含めた複合問題になることが多いです。そこで、二次関数の性質を使いながら問題を解けるようにしましょう。

特に二次関数で重要になるのが、$a$の値と変化の割合です。$a$の値によって、二次関数のグラフの形が変わります。また変化の割合を計算することで、2つの座標を通る直線の傾きを出すことができます。

世の中の自然現象で二次関数になっていることは多いです。二次関数の性質を学び、グラフの書き方や問題の解き方を理解するようにしましょう。