気体の溶解度とヘンリーの法則：圧力・物質量・体積の関係と公式の利用

気体は水に対して溶解度が非常に低いです。つまり、気体は水にわずかしか溶けません。ただ多少は溶けることができるため、どれだけ気体が水に溶けることができるのか計算できるようになりましょう。

気体の溶解度で重要なのがヘンリーの法則です。圧力が変化するとき、ヘンリーの法則を利用すれば、どれだけ気体が水に溶けるのか計算できます。

気体を水に溶かすのは、私たちが多くの場面で利用しています。例えば炭酸水では二酸化炭素が水に溶けています。ヘンリーの法則を利用することによって、二酸化炭素を水に溶かしているのです。

それでは、溶解度の低い気体がどれだけ水に溶けるのかについて、どのように計算すればいいのでしょうか。気体の溶解度では圧力や物質量、体積の関係が重要になります。そこで、これらの関係性を解説していきます。

気体の溶解度と分圧は比例する

通常、気体の水に対する溶解度は低いです。窒素や酸素、二酸化炭素は水に溶けるものの、少量の気体のみ溶けることができます。このとき、気体の溶解度は分圧と比例することが知られています。

例えば1Paで1つの分子が溶ける気体があるとします。この場合、2倍である2Paでは2つの分子が溶けます。また圧力が3倍になって3Paになると、3つの分子が溶けることができます。

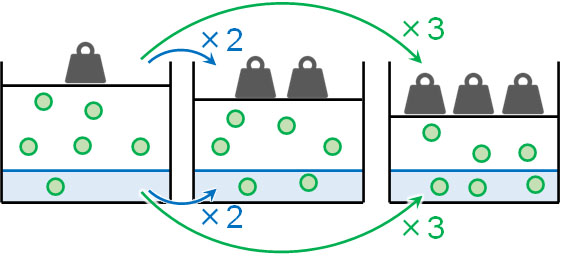
温度が同じ場合、圧力が増加すると、それに比例して溶ける気体の量が増えます。これをヘンリーの法則といいます。気体の溶解度を計算するとき、ヘンリーの法則を利用する必要があります。

・溶解度の高い気体はヘンリーの法則が成立しない

なおアンモニア（NH₃）や塩酸（HCl）など、水に対する溶解度が大きい気体はヘンリーの法則が成り立ちません。これらの気体は水と反応してイオンを生成するため、効率よく水に溶けるからです。

ヘンリーの法則が成り立つのは、窒素や酸素、二酸化炭素など、水と反応しない気体に限定されます。こうした気体の場合はイオンを作らず、水への溶解度は小さいです。そのため、ヘンリーの法則が成り立ちます。

炭酸飲料水の容器を開けると気泡が発生する理由

なお、ヘンリーの法則は多くの場面で利用されており、私たちにとって身近な例では炭酸水があります。

炭酸水というのは、水に二酸化炭素が溶けています。このとき炭酸飲料水やシャンパンなどでは、容器内の圧力を高めることによって多くの二酸化炭素が溶けるようにしています。

また炭酸飲料水やシャンパンのフタを開けると、二酸化炭素が勢いよく出てきます。シャンパンの場合、二酸化炭素が外に勢いよく出ることにより、シャンパンの液体まで外に飛び出してしまうこともあります。

フタを開けると二酸化炭素の分圧が低くなり、結果として液体の中に溶けていた二酸化炭素が空気中に放出されます。ヘンリーの法則というのは、私たちが日常的に経験している法則の一つです。

気体の溶解度は物質量で計算する：溶ける気体の体積は同じ

ヘンリーの法則で重要なのは、「溶ける気体の物質量が圧力と比例する」ことです。先ほど解説した図では、圧力が2倍になると、溶ける分子の量も2倍になっています。言い換えると、圧力が増えると溶ける気体の物質量が増加するのです。

一方、物質量ではなく体積に着目する場合はどうでしょうか。溶ける気体の体積については、圧力に関係なく一定です。ヘンリーの法則を学ぶとき、物質量と体積を区別していないと、確実に混乱してしまいます。

温度が同じの場合、圧力が2倍になると体積は\(\displaystyle\frac{1}{2}\)になります。これはつまり、2倍の分子が濃縮されていることを意味しています。また溶けることのできる気体の体積は同じなので、結果として2倍の物質量の気体が水に溶けます。

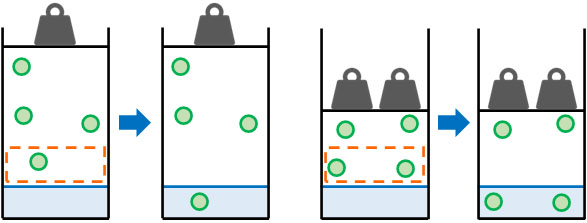
同様に、圧力が3倍になると体積は\(\displaystyle\frac{1}{3}\)になります。つまり、気体は3倍に濃縮されます。このとき、水に溶ける気体の体積は同じです。ただ、全体では3倍の物質量の気体が水に溶けます。

ヘンリーの法則では、温度が一定のとき、圧力が増えると溶ける気体の物質量が増加します。一方、溶ける気体の体積は変化しないことを理解しましょう。

ヘンリーの法則を利用して計算問題を解く

それでは、ヘンリーの法則を利用して計算問題を解いてみましょう。以下の問題の答えは何でしょうか。

• 1.0×10⁵Pa で20℃のとき、水1.0Lへの溶解度はO₂で1.3×10^-3mol です。温度を一定にして3.0×10⁵Pa の圧力をかけると、水1.0LへのO₂の溶解度はいくらでしょうか。

前述の通り温度が一定の場合、気体の溶解度は圧力に比例します。そこで、以下のように計算しましょう。

\(1.0×10^5:3.0×10^5=1.3×10^{-3}:x\)

\(x=3.9×10^{-3}\)

こうして、水1.0LへのO₂の溶解度は3.9×10^-3molと計算できます。

圧力を戻したときの体積を計算する

次に物質量ではなく、体積の問題を解いてみましょう。以下の問題の答えは何でしょうか。

• 1.0×10⁵Paで20℃のとき、O₂は水1.0Lへ0.031L溶け、O₂の溶解度は1.3×10^-3mol です。

1. 温度を一定にして3.0×10⁵Pa の圧力をかけると、水1.0Lへ溶ける酸素は何Lでしょうか。
2. 3.0×10⁵Paで溶けるO₂の体積というのは、1.0×10⁵Paでは何Lに相当するでしょうか。

1)

圧力を変化させても、水に溶ける酸素の体積は同じです。そのため、水へ溶ける酸素の体積は0.031Lです。

2)

3.0×10⁵Paで溶ける酸素の体積は0.031Lです。ただ、仮に3.0×10⁵Paを1.0×10⁵Paに変更する場合、気体は3倍に膨張します。そのため3.0×10⁵Paで0.031Lというのは、1.0×10⁵Paでは0.093Lに相当します。

\(0.031×3=0.093\)

混合気体ではそれぞれの分圧を利用して計算する

気体の溶解度を計算するとき、混合気体についても答えを得られるようにしましょう。混合気体の場合、分圧を計算することによって、溶けている気体の物質量をそれぞれ計算するといいです。

例えば、以下の問題の答えは何でしょうか。

• 27℃、1.0×10⁵PaにてN₂とO₂の混合気体があります。容器内に水が1.0Lあり、N₂とO₂の物質量の比が4:1のとき、それぞれ水に何mol溶けているでしょうか。なお、水1.0Lに溶ける気体の溶解度は27℃、1.0×10⁵PaでN₂が6.0×10^-4mol、O₂ が 1.2×10^-3molとします。

まず、窒素と酸素についてそれぞれの分圧はいくらでしょうか。物質量の比が「窒素：酸素＝4：1」であり、全圧が1.0×10⁵Paのため、それぞれの分圧は以下のようになるとわかります。

• 窒素の分圧：0.8×10⁵Pa
• 酸素の分圧：0.2×10⁵Pa

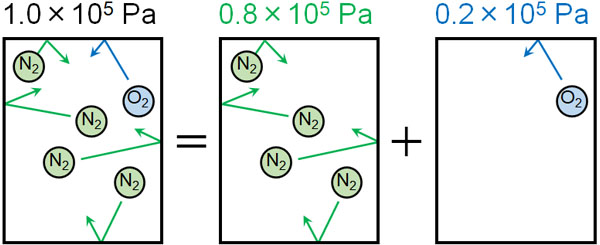
分圧がわかれば、それぞれの気体が溶けている量を計算できます。

・窒素の計算

1.0×10⁵PaでN₂は6.0×10^-4mol溶けることができます。それでは、0.8×10⁵Paではいくら溶けることができるでしょうか。以下のように比例式を利用して計算しましょう。

\(1.0×10^5:6.0×10^{-4}=0.8×10^5:x\)

\(x=4.8×10^{-4}\)

・酸素の計算

1.0×10⁵PaでO₂は1.2×10^-3mol溶けることができます。それでは、0.2×10⁵Paではいくら溶けることができるでしょうか。先ほどと同様に、比例式を利用して計算しましょう。

\(1.0×10^5:1.2×10^{-3}=0.2×10^5:x\)

\(x=2.4×10^{-4}\)

こうしてN₂は4.8×10^-4mol、O₂は2.4×10^-4molが溶けているとわかります。

ヘンリーの法則を用いて気体の溶解度を得る

水に対する溶解度が低い場合、ヘンリーの法則を利用することで溶解度の計算が可能です。窒素や酸素、二酸化炭素などはヘンリーの法則が有効です。

ヘンリーの法則を利用した現象は私たちが日常生活でひんぱんに経験しています。圧力が高いほど多くの気体が溶けるため、炭酸飲料水では容器内の圧力を高くしています。

なお、多くの人で混乱するのが圧力と体積の関係です。ヘンリーの法則では、圧力と気体の溶解度（物質量）が比例します。一方、圧力を変えたとしても水に溶ける気体の体積は一定です。そのため気体の溶解度を計算するとき、物質量と体積を区別しましょう。

気体の溶解度はヘンリーの法則を利用することによって計算できます。ヘンリーの法則を利用するときの注意点を理解し、気体の溶解度を計算しましょう。