原子核：ボーアの水素原子模型と電子のエネルギー準位

物理では原子を学びます。私たちは既に原子の構造を知っています。それでは、かつての科学者はどのように原子の構造を推測したのでしょうか。

原子の内部構造を理解するとき、重要な概念にボーアの水素原子模型があります。電子が波であると捉えることにより、電子が一定間隔で原子核の周囲に存在することがわかったのです。

またボーアの水素原子模型を利用することにより、電子が円軌道で原子核の周囲に存在する事実がわかるだけでなく、電子殻のエネルギー準位を計算することもできます。電子が光を吸収したり、放出したりする原理もわかります。

それでは、原子核と電子による構成はどのようになっているのでしょうか。原子の内部構造とボーアの水素原子模型、電子殻のエネルギー準位について解説していきます。

1 原子核と電子による構成を考える
- 1.1 トムソンのブドウパンモデルと長岡半太郎の土星型原子モデル
- 1.2 ラザフォードによる散乱実験：ラザフォードの原子模型
2 ボーアの水素原子模型とラザフォードの原子模型の欠点
- 2.1 電子の量子条件と量子数を得る公式：ボーアの量子条件
- 2.2 ボーアの水素原子模型を利用し、円軌道の半径を計算する
3 エネルギー準位の計算と公式
4 原子の構造を数式によって解き明かす

原子核と電子による構成を考える

物理や化学では、陽子や中性子、電子を学びます。また、原子核は陽子と中性子で構成されており、原子核の周囲に電子が存在することをあなたは既に知っています。

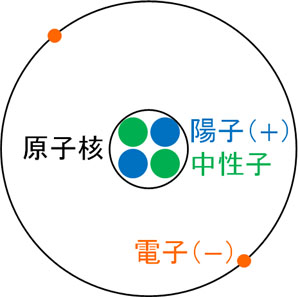
それでは、これらの事実が明らかでなかった時代で考えてみましょう。電子はマイナスの電荷をもっており、原子は中性です。そのため、原子には正電荷をもつ何かが存在するのは明らかです。この「正電荷である何か」を原子核と呼ぶことにしました。

原子（中性）＝原子核（正電荷）＋電子（負電荷）

それでは、原子核と電子はどのような配置になっていると当時の科学者は考えたのでしょうか。

トムソンのブドウパンモデルと長岡半太郎の土星型原子モデル

原子の質量はほとんど原子核が占めています。そのため、原子核は電子に比べて非常に大きいと考えることができます。

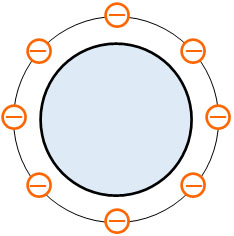
また原子核は正電荷であるため、薄く広がっている大きい正電荷に電子（負電荷）が静電気力によって結合しているとイギリスの物理学者であるトムソンは考えました。つまり、原子はブドウパンのような形をしているとトムソンは提唱したのです。

それに対して、日本の物理学者である長岡半太郎は原子の形として土星型原子モデルを提唱しました。原子核の周りを土星の惑星のように電子が回っていると彼は考えたのです。

静電気力の公式と万有引力の公式はそれぞれ以下のようになっています。

静電気力：\(F=k\displaystyle\frac{q_1q_2}{r^2}\)
万有引力：\(F=G\displaystyle\frac{mM}{r^2}\)

このように、公式は非常に似ています。そのため地球が月（衛星）を万有引力によって引き付けているのと同じように、サイズの大きい原子核（正電荷）がサイズの小さい電子（負電荷）を静電気力によって引き付けていると彼は考えたのです。

ラザフォードによる散乱実験：ラザフォードの原子模型

理論が正しいように思えたとしても、実験によって証明できない場合、その理論は役に立ちません。一方で考えられない理論であったとしても、実験によって証明できれば受け入れられます。原子の形についても、実験によって証明されれば、それが正しい理論となります。

原子の構造を確かめる実験はラザフォードによって行われました。彼は放射線の一種であるα粒子を利用して実験しました。α線は正電荷をもつため、この性質を利用してα粒子の軌道を確かめたのです。

トムソンのブドウパンモデルが正しい場合、原子核では正電荷が薄く広がっているため、静電気力は弱くアルファ粒子は通り抜けます。一方で長岡半太郎の土星型原子モデルが正しい場合、中心に強い正電荷をもつ原子核が存在するため、アルファ粒子は中心を通過できません。

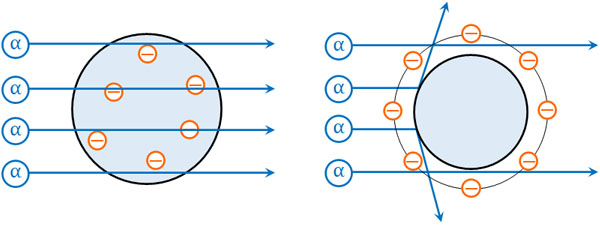
ラザフォードによる実験の結果、原子の中心でα粒子の散乱が起こり、原子の中心に正電荷をもつ物質が存在するとわかりました。つまり、トムソンのブドウパンモデルは間違っているとわかったのです。

ただラザフォードの実験により、長岡半太郎の土星型原子モデルも少し異なるとわかりました。長岡半太郎は中心に土星のような非常に大きい原子核が存在すると考えました。ただ実験をすると、原子核の大きさは原子に比べて非常に小さかったのです。

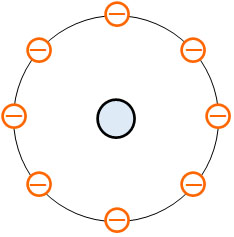
具体的には、原子核の大きさは原子の直径の1万分の1以下であるとわかったのです。こうして、非常に小さい原子核の周囲に電子が存在するとわかりました。これをラザフォードの原子模型といいます。

ボーアの水素原子模型とラザフォードの原子模型の欠点

ラザフォードの原子模型により、電子は原子核の周囲を回っていることがわかりました。そのためラザフォードの原子模型は問題ないように思えてしまいます。ただ実際には、ラザフォードの原子模型には矛盾点があります。ラザフォードの原子模型の何が問題なのでしょうか。

電子が加速度をもって動いている場合、電磁波（光）を放出することがわかっています。電磁波はエネルギーをもつため、電磁波を出す場合、その分だけエネルギーが減って電子は原子に引き寄せられます。

こうして、電子は円軌道を維持することができなくなります。つまり、時間が経過すると電子は原子核と合体してしまうのです。これが、ラザフォードの原子模型の欠点です。

ラザフォードの原子模型では、電子は原子核の周囲を回っており、具体的にどの軌道を回るのかは規定していませんでした。それに対して、ニールス・ボーアは電子の波動性についても考慮しました。彼は以下のように考えたのです。

電子が波として存在し、原子核の周囲に存在する電子殻上で回転する場合、電子は定常状態として安定して存在するため、電磁波を出さない。

この条件をボーアの量子条件といいます。つまり、電子が原子核の周囲を回転するとき、安定して存在するレーン（電磁波を出さず、定常状態で存在できるレーン）が存在するというわけです。

電子の量子条件と量子数を得る公式：ボーアの量子条件

それでは、ボーアの量子条件を計算してみましょう。電子が一つの波として存在するとき、下図のようにAとA’が同位相である必要があります。

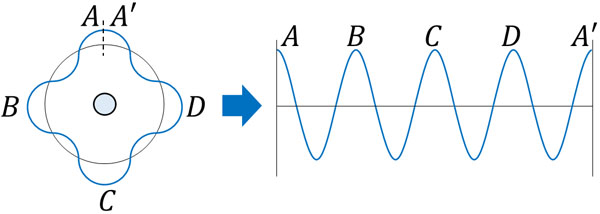
上図の場合、AとA’はつながることができるため、電子は一つの波となるのです。もし、AとA’の位相が少しでも異なると電子は波として存在することができません。位相が異なると波は打ち消し合うのです。一方で定常状態では波（電磁波）による打ち消し合いがなく、電磁波を出すことがなくなるのです。

なお半波長の偶数倍であれば、同位相となることで電子は波として存在することができます。電子が円を描くときの半径を\(r\)とすると、円周の長さは\(2πr\)です。そのため、\(2πr\)が半波長の偶数倍となるように以下の式を作りましょう。

\(2πr=\displaystyle\frac{λ}{2}×2n\) （\(n=1,2,3…\)）

注意点として、電子は先ほど示した図のように、波打ちながら原子核の周囲を回っているわけではありません。電子は波そのものであり、先ほどの図は波として存在するための性質（波長）を表しています。

・ボーアの量子条件を得る

なお、電子による波は物質波（ド・ブロイ波）です。そのため、物質波の公式である\(λ=\displaystyle\frac{h}{mv}\)を利用しましょう。先ほどの式に\(λ=\displaystyle\frac{h}{mv}\)を代入すると、以下のようになります。

\(2πr=n\displaystyle\frac{h}{mv}\) （\(n=1,2,3…\)）

※\(m\)は電子の質量、\(v\)は電子の速さ、\(h\)はプランク定数、\(n\)は量子数

この条件をボーアの量子条件といいます。この条件を満たす場合、電子は定常状態によって安定して原子核の周囲を回ることができます。

ボーアの水素原子模型を利用し、円軌道の半径を計算する

それでは、ボーアの水素原子模型を利用して円軌道の半径を計算してみましょう。先ほど説明した通り、静電気力は\(F=k\displaystyle\frac{q_1q_2}{r^2}\)によって計算できます。

電子の電気量を\(-e\)とすると、原子核は同じ電気量をもつため\(+e\)となります。また電子と原子核との半径が\(r\)の場合、静電気力は以下のようになります。

\(F=k_0\displaystyle\frac{e^2}{r^2}\)

※\(k_0\)は真空中のクーロン定数

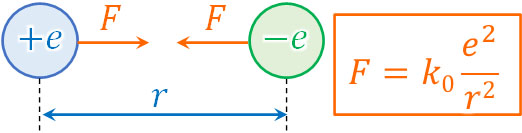
電子は原子核の周囲を回っているため、速さ\(v\)で等速円運動をしています。そのため、電子の質量を\(m\)、中心方向への加速度を\(a\)とすると、以下の式で表すことができます。

\(ma=k_0\displaystyle\frac{e^2}{r^2}\)

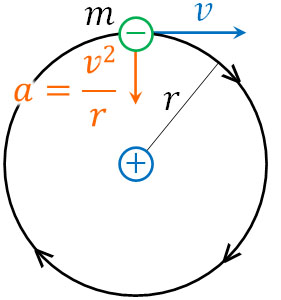
なお等速円運動の公式より、円の中心方向への加速度は\(a=\displaystyle\frac{v^2}{r}\)です。そこで、以下のように式を変形しましょう。

\(m\displaystyle\frac{v^2}{r}=k_0\displaystyle\frac{e^2}{r^2}\)

\(mv^2=k_0\displaystyle\frac{e^2}{r}\)

ただこの条件では、先ほど解説した通り、電子は電磁波を出すことによってエネルギーを放出してしまいます。そこで、この条件にボーアの量子条件を加えましょう。\(2πr=n\displaystyle\frac{h}{mv}\)を以下のように変形します。

\(2πr=n\displaystyle\frac{h}{mv}\)

\(v=\displaystyle\frac{nh}{2πrm}\)

そこで、\(v=\displaystyle\frac{nh}{2πrm}\)を\(mv^2=k_0\displaystyle\frac{e^2}{r}\)へ代入しましょう。

\(mv^2=k_0\displaystyle\frac{e^2}{r}\)

\(m×\displaystyle\frac{n^2h^2}{4π^2r^2m^2}=k_0\displaystyle\frac{e^2}{r}\)

\(\displaystyle\frac{n^2h^2}{4π^2m}=rk_0e^2\)

\(r=\displaystyle\frac{n^2h^2}{4π^2mk_0e^2}\)

こうして、電子の半径が\(r=\displaystyle\frac{n^2h^2}{4π^2mk_0e^2}\) （\(n=1,2,3…\)）のとき、電子はボーアの量子条件を満たすことで定常状態となります。

なお\(n\)を量子数と呼び、正の整数を代入することができます。また先ほどの式を確認すると、以下のように量子数\(n\)以外はすべて定数です。

プランク定数：\(h=6.6×10^{-34}\)
真空中のクーロン定数：\(k_0=9.0×10^9\)
電子の質量：\(m=9.1×10^{-31}\)
電気素量：\(e=1.6×10^{-19}\)
円周率：\(π=3.14\)

そのため\(n\)に正の整数を代入することにより、電子による円の軌道半径を計算できます。この電子による軌道が化学で学ぶK殻、L殻、M殻です。\(n=1\)を代入すると、K殻の半径を計算できます。また\(n=2\)を代入すると、L殻の半径を計算できます。

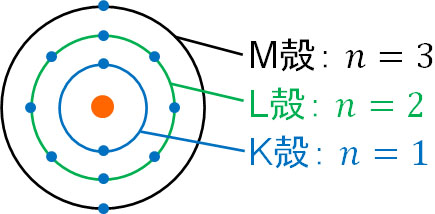
式を確認してわかる通り、電子殻の半径は\(n\)の二乗に比例します。そのため電子殻が大きくなると、原子核からの距離は大きく離れます。

なお電子による軌道で特定の電子殻（K殻、L殻、M殻）を学ぶのは、この軌道でなければ電子は波としての性質を示すことができず、定常状態となることができないからです。電子の軌道半径というのは、ボーアの水素原子模型を満たすことによって成立しているのです。

エネルギー準位の計算と公式

次に、電子が定常状態となっているときのエネルギー状態を確認しましょう。電子殻のそれぞれのレーン（K殻、L殻、M殻など）では、電子のエネルギー値が異なります。それぞれのレーンで電子がもつエネルギー値をエネルギー準位といいます。

それでは、原子核（電気量\(+e\)）の周りを質量\(m\)、電気量\(-e\)の電子が速さ\(v\)で回っている場合、電子がもつエネルギーはいくらでしょうか。電子は運動エネルギーをもち、さらには静電気力による位置エネルギーをもちます。

位置エネルギーは\(U=qV\)で計算できます。また点電荷（原子核の電気量である\(+e\)）によって起こる電圧は\(V=k_0\displaystyle\frac{e}{r}\)です。そのため、以下のように計算しましょう。

\(U=qV\)

\(U=-e×k_0\displaystyle\frac{e}{r}\)

\(U=-k_0\displaystyle\frac{e^2}{r}\)

そのため、電子がもつエネルギー\(E\)は以下のように表すことができます。

\(E=\displaystyle\frac{1}{2}mv^2-k_0\displaystyle\frac{e^2}{r}\)

電子の速度\(v\)が同じ場合、原子核と電子の距離\(r\)が近いほど静電気力が強くなって安定して存在できるため、\(k_0\displaystyle\frac{e^2}{r}\)による引き算するのは問題ないと思います。事実、L殻よりもK殻のほうがエネルギーは低いです。

なお先ほど記した通り、\(mv^2=k_0\displaystyle\frac{e^2}{r}\)なので、両辺に\(\displaystyle\frac{1}{2}\)をかけると\(\displaystyle\frac{1}{2}mv^2=k_0\displaystyle\frac{e^2}{2r}\)です。そこで、\(\displaystyle\frac{1}{2}mv^2=k_0\displaystyle\frac{e^2}{2r}\)をエネルギー\(E\)の式に代入しましょう。

\(E=\displaystyle\frac{1}{2}mv^2-k_0\displaystyle\frac{e^2}{r}\)

\(E=k_0\displaystyle\frac{e^2}{2r}-k_0\displaystyle\frac{2e^2}{2r}\)

\(E=-k_0\displaystyle\frac{e^2}{2r}\)

こうして、\(E=-k_0\displaystyle\frac{e^2}{2r}\)を得ることができました。

なお先ほど、\(r=\displaystyle\frac{n^2h^2}{4π^2mk_0e^2}\)であると計算しました。そこで、\(r=\displaystyle\frac{n^2h^2}{4π^2mk_0e^2}\)を\(E=-k_0\displaystyle\frac{e^2}{2r}\)に代入しましょう。

\(E=-k_0\displaystyle\frac{e^2}{2r}\)

\(E=-k_0\displaystyle\frac{e^2}{2}×\displaystyle\frac{4π^2mk_0e^2}{n^2h^2}\)

\(E=-\displaystyle\frac{2π^2mk_0^2e^4}{h^2}·\displaystyle\frac{1}{n^2}\)

式を確認すると、量子数\(n\)以外は定数です。つまり電子のエネルギー準位というのは、どの電子殻（K殻、L殻、M殻など）に入るのかによって決まります。

振動数条件：基底状態と励起状態

当然ながら、電子は最も低いエネルギーを保とうとします。例えば水素原子であれば、K殻に電子を1つもちます。酸素原子であればK殻に電子を2つ、L殻に電子を6つもちます。このような最も低いエネルギーとなる状態を基底状態といいます。

化学では、電子はK殻に入り、次にL殻に入り、次にM殻に入ると学びます。この理由としては、外側の電子殻にある電子はエネルギー準位が高くなるからです。

それでは、原子に存在する電子が常に基底状態となっているかというと、そういうわけではありません。光エネルギーを受け取ることにより、電子が外側の電子殻へ移動することがあります。電子が光子からエネルギーを受け取り、エネルギーの高い電子殻に存在する状態を励起状態（れいきじょうたい）といいます。

光子がもつエネルギーは\(hν\)です。そのため電子は\(hν\)のエネルギーを受け取り、基底状態から励起状態となります。

なお励起状態は不安定であるため、電子はエネルギーとして光子を放出します。光子を吸収して基底状態から励起状態になるというのは、光子を放出して励起状態から基底状態へ戻れることを意味しているのです。このとき電子が放出するエネルギーは\(hν\)です。

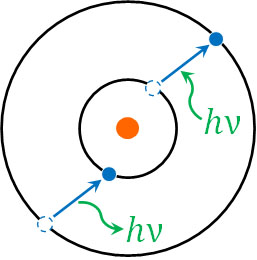
なお先ほど説明した通り、電子のエネルギー準位はどの軌道に存在するのかによって決まります。つまり「K殻とL殻のエネルギー差」や「L殻とM殻のエネルギー差」は決まっています。

またエネルギー準位の異なる軌道へ電子が移動するとき、光子のエネルギー\(hν\)を吸収または放出することになります。そのため、エネルギー準位の差と光子のエネルギー\(hν\)がぴったり合うとき、電子は他の軌道へ移動します。

例えば、基底状態にある電子が第\(n\)レーン（量子数\(n\)）にいるとします。このとき光子から\(hν\)のエネルギーを吸収し、第\(n’\)レーン（量子数\(n’\)）へ移り、励起状態になります（\(n<n’\)）。

この場合、\(hν\)が電子のエネルギー準位の差になるため、量子数\(n\)のエネルギー準位を\(E_n\)、量子数\(n’\)のエネルギー準位を\(E_n’\)とすると、以下の式を作ることができます。

\(hν=E_n’-E_n\)

この条件を振動数条件といいます。なお、電子がどの電子殻に移動するにしても、エネルギーの受け渡しで利用される光子は一つです。

原子のスペクトルとリュードベリ定数：ボーア半径

それでは、エネルギー準位の差に関する式を変形しましょう。光量子仮説の公式より、\(E=hν=h\displaystyle\frac{c}{λ}\)です。そのため、先ほどの式を以下のように変えることができます。

\(h\displaystyle\frac{c}{λ}=E_n’-E_n\)

また先ほど計算した通り、量子数が\(n\)のとき、電子がもつエネルギーは\(E=-\displaystyle\frac{2π^2mk_0^2e^4}{h^2}·\displaystyle\frac{1}{n^2}\)です。そのため、式は以下のようになります。

\(h\displaystyle\frac{c}{λ}=-\displaystyle\frac{2π^2mk_0^2e^4}{h^2}·\displaystyle\frac{1}{n’^2}\)\(+\displaystyle\frac{2π^2mk_0^2e^4}{h^2}·\displaystyle\frac{1}{n^2}\)

\(h\displaystyle\frac{c}{λ}=\displaystyle\frac{2π^2mk_0^2e^4}{h^2}\left(\displaystyle\frac{1}{n^2}-\displaystyle\frac{1}{n’^2}\right)\)

\(\displaystyle\frac{1}{λ}=\displaystyle\frac{2π^2mk_0^2e^4}{h^3c}\left(\displaystyle\frac{1}{n^2}-\displaystyle\frac{1}{n’^2}\right)\)

この式について、\(\displaystyle\frac{2π^2mk_0^2e^4}{h^3c}\)に含まれる値は決まっており、定数と考えることができます。そこで、\(R=\displaystyle\frac{2π^2mk_0^2e^4}{h^3c}\)としましょう。

なお、定数\(R\)をリュードベリ定数といいます。リュードベリ定数は\(R≒1.1×10^7\)[m^-1]です。リュードベリ定数を利用して式を記すと以下のようになります。

\(\displaystyle\frac{1}{λ}=R\left(\displaystyle\frac{1}{n^2}-\displaystyle\frac{1}{n’^2}\right)\)

こうして、電子が吸収または放出する光子の波長\(λ\)の逆数を計算できる公式を得ることができました。ボーアの理論を利用することにより、水素原子で起こる現象を説明できるのです。

原子ごとに、吸収・放出する光の波長は決まっている

リュードベリ定数\(R\)は値が決まっているため、基底状態の量子数\(n=1\)と励起状態の量子数\(n’\)が決まれば、水素原子が吸収または放出する光子の波長が決まります。つまり、水素原子で電子が励起状態から基底状態に戻るとき、特定の波長でしか光を発することができません。

なお水素に限らず、ほかの原子についても、励起状態から基底状態に電子が戻るときに発することのできる光の波長\(λ\)は決まっています。これを線スペクトルといいます。

線スペクトルは原子によって特有であるため、発せられる光が可視光の場合、光を見分けることによって原子の種類を判断できます。これを炎色反応といいます。

炎色反応では、色を見極めることによって含まれている元素を確認できます。この理由としては、エネルギーを与えて励起状態にした後、電子が基底状態に戻るときに発する光の波長（光の色）が決まっているからなのです。

なお電子のエネルギー準位の差\(hν\)は原子によって決まっており、光エネルギーを発するときだけでなく、光エネルギーを吸収するときも特定波長\(λ\)の光のみを吸収します。

原子が含まれている場合、光を当てると特定の波長のみ観察されなくなります。この理由として、原子は特定の波長のみ吸収するからです。吸収されたエネルギーは電子が励起状態になるために利用されます。これを吸収スペクトルといいます。

そのため吸収スペクトルを調べることにより、どの原子が含まれているのか把握できます。吸収スペクトルは分析化学など多くの分野で利用されており、原子が特定波長の光を吸収する性質を利用しています。

水素のイオン化エネルギーを計算する

それでは、水素のイオン化エネルギーを計算してみましょう。水素がイオンになると、H⁺となります。つまり、水素原子に電子は存在しません。そのため、量子数\(n’\)の値は∞になります。

また基底状態では、水素の量子数は\(n=1\)です。そこで\(n=1\)、\(n’=∞\)を利用してエネルギー差を計算しましょう。

\(E_n’-E_n=0-\left(-\displaystyle\frac{2π^2mk_0^2e^4}{h^2}·\displaystyle\frac{1}{1^2}\right)\)

\(=\displaystyle\frac{2π^2mk_0^2e^4}{h^2}\)

こうして、水素のイオン化エネルギーは\(\displaystyle\frac{2π^2mk_0^2e^4}{h^2}\)とわかりました。なおリュードベリ定数は\(R=\displaystyle\frac{2π^2mk_0^2e^4}{h^3c}\)であるため、先ほどの答えを\(E_n’-E_n=hcR\)としても正解です。

参考までに、\(E_n’-E_n=hcR\)は実験によって得られる水素のイオン化エネルギーと一致します。物理では、実験と一致すれば正しい理論として受け入れられます。そのため私たちが原子を学ぶとき、ボーアの水素原子模型が重要になるのです。