粒子として存在している物質であっても、波としての性質があります。粒子と波は相反する性質であるものの、すべての物質には粒子性と波動性があるのです。
物質が波として存在するとき、この波を物質波(ド・ブロイ波)といいます。電子など、非常に小さい物質は波として取り扱うことが可能なのです。通常、共存が不可能に思ってしまう粒子性と波動性ですが、すべての物質が波として扱えることができるのです。
粒子が波としての性質をもつのは、電子による干渉(ブラッグ反射)によって実験で証明されています。実験で明らかになっている以上、この事実を私たちは受け入れなければいけません。
それでは、どのように物質波に関する公式を利用すればいいのでしょうか。また、「粒子が波である」というのは、何を意味するのでしょうか。物体がもつ波動性について解説していきます。
もくじ
物質には波としての性質がある
粒子と波は性質が異なります。粒子は衝突することにより、反発します。一方で2つの波が重なっても反発することはなく、波は互いに独立しています。このように、粒子と波の性質は大きく異なります。
ただアインシュタインが光量子仮説を提唱し、光電効果が起こる理由を説明しました。また実験により、光は波としての性質をもつことが明らかになりました。そこでフランスの物理学者であるド・ブロイは次のように考えました。
- 光が粒子としての性質をもつのであれば、電子など粒子と考えられている物質も波としての性質がある。
アインシュタインが提唱した光量子仮説と同様に奇想天外な発想であったため、このド・ブロイの考えは当初、受け入れられませんでした。ただ実験によって電子の波動性が明らかになり、電子の波動性を発見した人物として彼はノーベル物理学を受賞しました。
粒子が波としてふるまうとき、この波を物質波(ド・ブロイ波)といいます。波として扱うため、電子などの粒子は波長\(λ\)をもつことになります。
物質波(ド・ブロイ波)の公式
それでは、ド・ブロイ波の公式には何があるのでしょうか。粒子の波長\(λ\)を得る公式を導出しましょう。物質波の公式を覚える必要はなく、コンプトン効果で利用する公式を変形すればいいです。
コンプトン効果では、光を粒子と捉えることで運動量保存則を利用します。光の粒子がもつ運動量\(p\)は以下の公式によって計算できます。
- \(p=\displaystyle\frac{hν}{c}=\displaystyle\frac{h}{λ}\)
この公式を以下のように変形しましょう。
\(p=\displaystyle\frac{h}{λ}\)
\(λ=\displaystyle\frac{h}{p}\)
こうして、公式として\(λ=\displaystyle\frac{h}{p}\)を得ることができました。なお、質量\(m\)の物質が速さ\(v\)で動いているとき、運動量は\(p=mv\)です。
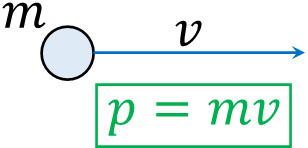
そのため、以下の公式を作ることができます。
- \(λ=\displaystyle\frac{h}{mv}\)
こうして、コンプトン効果で利用される公式と運動量の公式を変形することにより、物質波の計算で利用される公式を導出できます。物質波を計算するとき、新たに公式を覚える必要はありません。
人を波と捉えられるものの、値が小さくて認識できない
物質波(ド・ブロイ波)というのは、すべての物質に利用できます。\(λ=\displaystyle\frac{h}{mv}\)を見てわかる通り、質量と速さをもつ物質であれば波として捉えることができるのです。
そのため、人を波と捉えることもできます。ただ、私たちが日常生活で人や物体が波であると感じることはありません。この理由として、値が小さすぎて認識できないからです。
例えば、1.0m/sで歩いている体重66kgの人の波動性を計算しましょう。プランク定数は\(h≒6.6×10^{-34}\)[J·s]なので、以下のように計算できます。
\(λ=\displaystyle\frac{h}{mv}\)
\(λ=\displaystyle\frac{6.6×10^{-34}}{66×1}\)
\(λ=1.0×10^{-35}\)
このように、波長の長さは1.0×10-35mです。非常に小さい波であり、私たちの目で確認することはできません。これが、私たちが日常生活でド・ブロイ波を感じない理由です。物質波というのは、電子など非常に小さい物質で利用できるのです。
要は、万有引力と同じです。万有引力はすべての物質に働くものの、値が非常に小さいので私たちが日常生活で万有引力を感じることはありません。万有引力は地球などのように、非常に大きい物質で利用できます。物質波も同様であり、ド・ブロイ波は非常に小さい物質で利用できます。
光の干渉(ブラッグ反射)を観察することで物質波を観測する
なお、物理では理論が正しくても実験によって証明されなければ人々に受け入れてもらえません。一方、どれだけ理論の飛躍があっても、実験によって証明されれば、すべての人に受け入れられます。物質波がすべての物理の教科書に記載されているのは、実験によって証明されたからなのです。
具体的には、ブラッグ反射によって電子の粒子性が証明されました。X線は電磁波の一種であり、粒子性があると同時に、波としての性質があります。そのためX線を結晶に当てると、散乱することによってラウエ斑点(X線による干渉)を生じます。
X線の散乱によって波が強め合い、以下のようなラウエ斑点をスクリーンで観察できるのです。
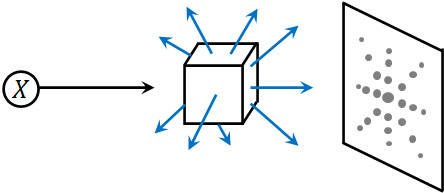
干渉は波に特有の現象です。そこで電子を結晶に当てて散乱させることにより、ラウエ斑点を観察できれば、電子には粒子性だけでなく、波動性をもつとわかります。
この仮説をもとに実験をすると、電子を用いてラウエ斑点を観察することができました。こうして、ド・ブロイの考えは正しかったと証明されました。
アインシュタインによる光量子仮説により、「波と考えられていた光(電磁波)には粒子性がある」とわかりました。またド・ブロイにより、「粒子と考えられていた電子には波動性がある」とわかりました。こうして、すべての物質は粒子性と波動性の両方の性質があるとわかったのです。
光量子仮説や物質波を学ぶと、X線や電子など、非常に小さいミクロの世界では、常識が通用しない法則がたくさん存在するとわかります。そこで、ミクロの世界を研究する分野として量子力学が生まれ、発展していったのです。なお、量子力学は大学物理で詳しく学びます。
物質波に関する練習問題
それでは、物質波(ド・ブロイ波)に関わる練習問題を解いてみましょう。公式を利用することにより、波長\(λ\)や電圧\(V\)を計算するのです。以下の問題の答えは何でしょうか。
- 静止している質量\(m\)、電荷\(-e\)の電子に対して、電圧\(V\)をかけて加速させたところ、速さ\(v\)となりました。なお、プランク定数を\(h\)とします。
- 電子の波長\(λ\)を求めましょう。
- 電圧\(V\)を大きくすると、電子の波長\(λ\)はどのように変化しますか。
- ブラッグ反射の条件と同様に\(2dsinθ=nλ\)(\(n=1,2,3…\))を電子に適用できる場合、反射強度がピークとなる電子の加速電圧\(V\)はいくらですか。
1) 電子の波長\(λ\)を求めましょう
電子の電荷が\(-e\)であり、電圧が\(V\)なので、静電気力の位置エネルギーは\(U=eV\)です。このエネルギーがすべて運動量に変わるため、以下の計算をしましょう。
\(eV=\displaystyle\frac{1}{2}mv^2\)
\(v^2=\displaystyle\frac{2eV}{m}\)
\(v=\sqrt{\displaystyle\frac{2eV}{m}}\)
次に、先ほど解説したド・ブロイ波で利用される公式を利用しましょう。
\(λ=\displaystyle\frac{h}{mv}\)
\(λ=\displaystyle\frac{h}{m}×\sqrt{\displaystyle\frac{m}{2eV}}\)
\(λ=\displaystyle\frac{h}{\sqrt{2meV}}\)
こうして、\(λ=\displaystyle\frac{h}{\sqrt{2meV}}\)であるとわかりました。
2) 電圧\(V\)を大きくすると、電子の波長\(λ\)はどのように変化しますか
\(λ=\displaystyle\frac{h}{\sqrt{2meV}}\)を確認してわかる通り、電圧\(V\)を大きくすると、電子の波長\(λ\)は小さくなります。
3) ブラッグ反射の条件と同様に\(2dsinθ=nλ\)(\(n=1,2,3…\))を電子に適用できる場合、反射強度がピークとなる電子の加速電圧\(V\)はいくらですか
X線を用いたブラッグ反射の条件では、位相は同じであるため、経路差が半波長の偶数倍であれば2つの光が強め合います。そのため\(2dsinθ=\displaystyle\frac{λ}{2}×2n\)と表すことができ、\(2dsinθ=nλ\)となります。
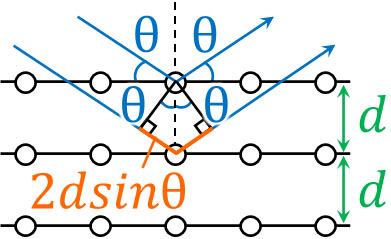
電子を波と捉え、X線と同様にブラッグ反射するのであれば、電子の波が強め合う条件はブラッグの式に従って\(2dsinθ=nλ\)となります。そのため、電子の波長\(λ\)を満たす電圧\(V\)を計算しましょう。\(λ=\displaystyle\frac{h}{\sqrt{2meV}}\)を利用すると、以下のようになります。
\(2dsinθ=nλ\)
\(λ=\displaystyle\frac{2dsinθ}{n}\)
\(\displaystyle\frac{h}{\sqrt{2meV}}=\displaystyle\frac{2dsinθ}{n}\)
\(\displaystyle\frac{h^2}{2meV}=\displaystyle\frac{4d^2sin^2θ}{n^2}\)
\(V=\displaystyle\frac{n^2h^2}{8med^2sin^2θ}\)
こうして、電子の波が強め合うときの電圧(反射強度がピークとなる電子の加速電圧\(V\))は\(V=\displaystyle\frac{n^2h^2}{8med^2sin^2θ}\)であると計算できました。
すべての物体は波動性をもつ
人を含め、すべての物体が波としての性質をもつとなると、多くの人は信じることができません。ただ、ミクロの世界では電子が波動性を示すことが実験で証明されているため、私たちはこの事実を信じる必要があります。
ド・ブロイは電子に波動性があると考え、これによって物質波(ド・ブロイ波)という概念が生まれました。こうして、量子力学が発展していったのです。
物質波で利用される公式を覚える必要はありません。コンプトン効果で利用される公式を変形すれば、物質波で使われる公式を導出できます。そこで、エネルギー保存則やブラッグの式を利用して計算問題を解けるようになりましょう。
物質波の発見により、多くの常識が覆されることになりました。こうして光量子仮説や物質波の概念が提唱され、量子力学が発展していったのです。






