2つの物体が衝突するとき、物理で利用される概念に運動量があります。2つの物体が衝突すると、その後のスピードは変化します。このとき、運動量を利用して衝突後の速度を計算できます。
運動量の計算をするとき、必ず力積を理解しなければいけません。物質に対して力積が加わることにより、速度が速くなります(または速度が遅くなります)。
また運動と力積で学ぶ重要な内容が運動量保存則です。2つの物体が衝突する前後では、運動量の総和は同じです。この法則を利用することにより、衝突後の速度を計算できるのです。作用・反作用による力のみが働く場合、運動量保存則が有効です。
なお、運動量保存則は力学的エネルギー保存則と似ています。ただ、両者は明確に分けて使わなければいけません。そこで運動量の詳細や運動量保存則の使い方、力学的エネルギー保存則との違いを解説していきます。
もくじ
運動量と力積の関係
衝突するためには、2つの物体が存在しなければいけません。1つの物体だけで衝突することはできません。1つの物体ではなく、2つの物体が関係していることが非常に重要であり、2つの物体が衝突している場面で運動量を利用しましょう。
運動量とは、運動の激しさを表します。また運動量\(p\)は質量\(m\)と速度\(v\)を利用して以下のように表されます。
- \(\overrightarrow{p}=m\overrightarrow{v}\)
公式を見てわかる通り、運動の激しさは質量と速度で決まります。例えば速度が同じであっても、軽い物質では衝撃が小さく、重い物体では衝撃が大きいです。同じ速度であっても、ピンポン玉が衝突するよりも、車が衝突するほうが衝撃は大きいです。これを公式で表しているのが運動量です。
また質量が同じであっても、速度が速いと物体は激しく運動します。例えば軽い物体であっても、銃弾のように速度が速い場合、衝撃は大きくなります。
加わる力の合計が力積
1つの物体に力を加えることで速度が変化するとき、どれだけの力を加えたのかを表す指標に力積があります。物体が\(t\)秒間、力\(F\)を受ける場合、力積は以下のように表されます。
- 力積\(=Ft\)
1つの物体に対して力(衝撃)を加え、速度を変化させるにしても、力を加える時間によって衝突後の速度は違います。同じ力を加えるにしても、力を1秒加えるのと、力を5秒加えるのでは、当然ながら力を5秒加えたほうが速度は速くなります。

そのため速度の変化では、力の大きさと力を与える時間の両方を考慮した力積を用いて計算する必要があるのです。
運動量と力積の関係を理解する
それでは、なぜ運動量と力積を同時に学ぶ必要があるのでしょうか。運動量と力積にはどのような関係性があるのでしょうか。
一定の力\(F\)を\(t\)秒間、受けるときに力積を計算できます。力\(F\)というのは、運動方程式より\(F=ma\)で表すことができます。つまり、加速度\(a\)を以下のように表せます。
\(F=ma\)
\(a=\displaystyle\frac{F}{m}\)
このとき力\(F\)と質量\(m\)は一定であるため、加速度\(a\)は一定です。つまり、等加速度直線運動をしています。そこで等加速度直線運動の公式を利用して、\(a=\displaystyle\frac{F}{m}\)を代入しましょう。以下のようになります。
\(v=v_0+at\)
\(v=v_0+\displaystyle\frac{F}{m}t\)
\(Ft=mv-mv_0\)
質量\(m\)と速さ\(v\)をかけると運動量を得られます。つまり、\(mv\)と\(mv_0\)は運動量を表します。また\(mv\)は衝突後の運動量、\(mv_0\)は衝突前の運動量です。つまり、力積\(Ft\)は衝突後の運動量\(mv\)から衝突前の運動量\(mv_0\)を引くことによって得られます。
- 力積 = 変化後の運動量 - 変化前の運動量
または、先ほどの公式\(Ft=mv-mv_0\)を以下のように変形することもできます。
- \(mv_0+Ft=mv\)
質量\(m\)で初速度\(v_0\)の物体に対して、力積\(Ft\)を加えると、運動量が\(mv\)になることをこの式は表しています。
- 変化前の運動量 + 力積 = 変化後の運動量
衝突後の運動量というのは、衝突前の運動量に力積を加えることで得られます。また力積を計算するとき、前述の通り変化後の運動量から変化前の運動量を引くことによって得られます。
運動量の計算ではベクトルが重要
なお運動量の計算をするとき、必ずベクトルを意識しましょう。先ほど、運動量\(p\)の公式を記すとき、\(p=mv\)ではなく以下のように記しました。
- \(\overrightarrow{p}=m\overrightarrow{v}\)
これには、当然ながら意味があります。運動量\(p\)を計算するとき、公式に矢印が存在することが重要です。
例えば右向きに運動している物体に対して、さらに右向きの力を加えると、右方向へ加速します。一方、右向きに運動している物体に対して、下から力を加えると、物体は右上に進みます。ただ、右方向の速度に変化はありません。
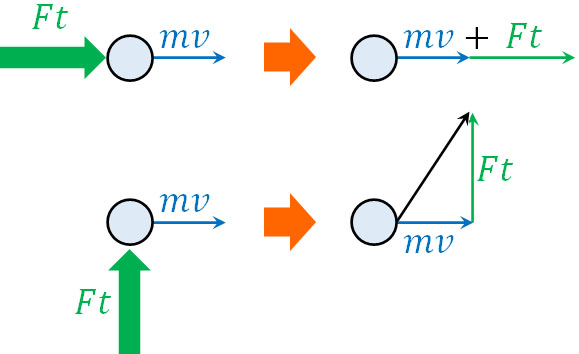
運動量の計算をするとき、物体の運動方向と力が同じ向き(または反対向き)である必要があります。物理では、運動の向きや力の向きが重要になり、ベクトルが異なる場合は力を分解しなければいけません。これは運動量や力積でも同様です。
運動量と力積の関係は仕事とエネルギーの関係と似ている
運動量と力積の関係というのは、仕事とエネルギーの関係と似ています。前述の通り、運動量と力積には以下の関係があります。
- \(mv_0+Ft=mv\)
- 変化前の運動量 + 力積 = 変化後の運動量
それに対して、仕事とエネルギーの関係は以下になります。
- \(\displaystyle\frac{1}{2}mv_0^2+Fx=\displaystyle\frac{1}{2}mv^2\)
- 変化前のエネルギー + 仕事 = 変化後のエネルギー
運動量と仕事は概念が異なります。ただ力学で計算問題を解くとき、運動量と仕事の2つを利用することがひんぱんにあります。そこで、2つセットで理解しましょう。
運動量保存則:作用・反作用の力のみが働くときに利用できる
それでは、どのようなときに運動量を利用できるのでしょうか。運動量を利用して計算するとき、最も重要な法則が運動量保存則です。衝突前と衝突後の2物体を比べると、運動量の和が等しくなるのが運動量保存則です。
質量\(m_1\)の物体1と質量\(m_2\)の物体2について、衝突前の速度を\(v_1,v_2\)、衝突後の速度を\(v_1′,v_2’\)とすると、運動量保存則の公式は以下になります。
- \(m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\)
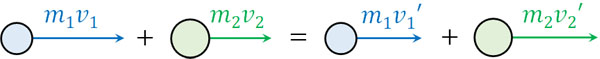
運動量保存則を利用できるのは、2つの物体に作用・反作用による力のみが働くケースです。
2つの物体が衝突すると、物体1は物体2から力\(F\)を受けます。同様に、作用・反作用の法則によって物体2は物体1から力\(F\)を受けます。力を受ける時間\(t\)は同じです。また、物体2が受ける力積を\(Ft\)とすると、物体1が受ける力積は\(-Ft\)です。
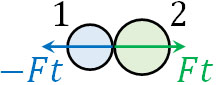
そこで、それぞれの物体と力積の関係を式にすると以下のようになります。
- 物体1:\(m_1v_1-Ft=m_1v_1’\)
- 物体2:\(m_2v_2+Ft=m_2v_2’\)
次に、2つの式を足しましょう。そうするとき、先ほどの公式を得ることができます。
- \(m_1v_1+m_2v_2=m_1v_1’+m_2v_2’\)
- 衝突前の運動量の和 = 衝突前の運動量の和
衝突する前後で運動量の和が同じであることを利用するとき、前述の通り作用・反作用の力のみが働いているかどうかが重要です。言い換えると、外から加えられる力がない場合、運動量保存則が成り立ちます。
2つの物体が衝突するときの運動量と力積
なお力学を学ぶとき、実際に問題を解かなければ式を作ることができません。そこで問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 質量\(2m\)のボールAが速さ\(v\)でなめらかな床を動いており、静止している質量\(m\)のボールBに衝突しました。衝突前の進行方向に対して、下図のようにボールAは衝突後に60°の角度、ボールBは衝突後に30°の角度で進みました。ボールAとボールBの速度はいくらですか。
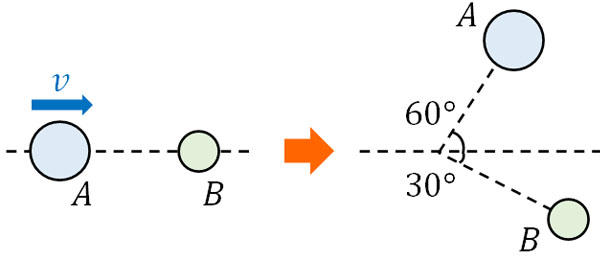
2つの物体が衝突するとき、働く力は作用・反作用のみです。そのため、運動量保存則を利用して式を作りましょう。衝突後の速度をそれぞれ\(v_A\)、\(v_B\)とすると、運動量保存則より、\(x\)軸方向と\(y\)軸方向で以下の式を作ることができます。
・\(x\)軸方向
\(2mv=2mv_Acos60°+mv_Bcos30°\)
\(2mv=mv_A+\displaystyle\frac{\sqrt{3}}{2}mv_B\)
\(2v=v_A+\displaystyle\frac{\sqrt{3}}{2}v_B\)
・\(y\)軸方向
\(0=2mv_Asin60°-mv_Bsin30°\)
\(mv_B=2\sqrt{3}mv_A\)
\(v_B=2\sqrt{3}v_A\)
そこで、\(v_B=2\sqrt{3}v_A\)を\(2v=v_A+\displaystyle\frac{\sqrt{3}}{2}v_B\)に代入しましょう。
\(2v=v_A+\displaystyle\frac{\sqrt{3}}{2}v_B\)
\(2v=v_A+\displaystyle\frac{\sqrt{3}}{2}×2\sqrt{3}v_A\)
\(2v=4v_A\)
\(v_A=\displaystyle\frac{v}{2}\)
また\(v_A=\displaystyle\frac{v}{2}\)なので、\(v_B=\sqrt{3}v\)と計算できます。こうして、運動量保存則を利用することによって衝突後の速さがわかりました。
運動量保存則と力学的エネルギー保存則の使い分け
それでは、運動量保存則と力学的エネルギー保存則はどのように使い分ければいいのでしょうか。両者の使い方を理解していないと、計算問題を解くことができません。また、公式を利用する場面を間違うと誤答になります。
運動量保存則というのは、ここまで解説した通り、2つの物体が衝突する場面で利用します。より正確には、作用・反作用の力が働く場面にのみ利用されます。
- 2つの物体が衝突する
- 物体の上をほかの物体がすべり、摩擦力が発生する
- 物体が内部で分裂し、2つの物体に分かれる

これらの場面に共通しているのは、作用・反作用の力のみが働いている点です。2つの物体が衝突、合体、分裂するとき、運動量保存則を利用しましょう。
・力学的エネルギー保存則は1つの物体、または衝突のないケースで利用する
それに対して、力学的エネルギー保存則はどのような場面で利用されるのでしょうか。運動量保存則とは異なり、力学的エネルギー保存則は基本的に1つの物体で利用されます。
なお、力学的エネルギー保存則を2つの物体で利用することは可能です。ただ2つの物体が関わる場合、衝突や合体、分裂がないケースで力学的エネルギー保存則が利用されます。
力学的エネルギー保存則というのは、エネルギーを取り扱います。エネルギーには熱や音も存在し、例えば摩擦がある場合は摩擦熱としてエネルギーが放出されてしまいます。つまり、摩擦力がある場面で力学的エネルギー保存則を利用することはできません。
物体が衝突、合体、分裂する場合、一部は熱や音などのエネルギーに変わります。そのため、力学的エネルギー保存則を利用できないのです。運動量保存則と力学的エネルギー保存則を学ぶとき、この違いを認識することが重要です。
運動量保存則と力学的エネルギー保存則を利用する練習問題
それでは、運動量保存則と力学的エネルギー保存則を利用して問題を解きましょう。2つの使い分けをすることで正解を得ることができます。以下の問題の答えは何でしょうか。
- 質量\(m\)の物体を高さ\(h\)の斜面上に置き、手を離すと加速しました。また、下図のように壁にはばね定数\(k\)のばねが存在し、ばねには質量\(m\)の板が取り付けられています。摩擦力は存在せず、重力加速度を\(g\)とするとき、以下の問題に答えましょう。
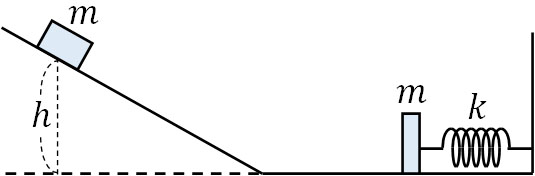
- 物体が板に衝突する直前の速度を求めましょう。
- 物体が衝突後、板と一体になって振動する場合、衝突直後の速度を求めましょう。
- ばねの縮みの最大距離\(x\)を求めましょう。
1) 物体が板に衝突する直前の速度を求めましょう
物体が衝突する前では、一つの物体による運動です。そのため、力学的エネルギー保存則を利用しましょう。求める速度を\(v\)とすると、以下のようになります。
\(mgh=\displaystyle\frac{1}{2}mv^2\)
\(v^2=2gh\)
\(v=\sqrt{2gh}\) (\(v>0\))
位置エネルギーがすべて運動エネルギーへ変わることにより、\(v=\sqrt{2gh}\) とわかりました。
2) 物体が衝突後、板と一体になって振動する場合、衝突直後の速度を求めましょう
衝突前とは異なり、衝突後では物体と板が一緒に振動するため、合計の重さは\(2m\)になります。また2つの物体が衝突するため、力学的エネルギー保存則ではなく、運動量保存則を利用しましょう。衝突直後の速度を\(V\)とすると、以下のように式を作ることができます。
\(mv=2mV\)
\(\sqrt{2gh}=2V\)
\(V=\displaystyle\frac{\sqrt{2gh}}{2}\)
運動量保存則を利用することで、\(V=\displaystyle\frac{\sqrt{2gh}}{2}\)とわかりました。
3) ばねの縮みの最大距離\(x\)を求めましょう
物体と板は一緒に振動しているため、質量\(2m\)の物体とみなすことができます。またばねの縮みが最大距離になるため、運動エネルギーがすべて弾性エネルギーに変わります。そこで、以下の式を作りましょう。
\(\displaystyle\frac{1}{2}·2mV^2=\displaystyle\frac{1}{2}kx^2\)
注意点として、\(mgh=\displaystyle\frac{1}{2}kx^2\)の式を作ってはいけません。2つの物体が衝突するとき、前述の通り熱や音としてエネルギーが逃げます。つまり、力学的エネルギー保存則が成立していません。
そこで、衝突直後の速度\(V\)を利用しましょう。この場合、物体と板を一つの物体とみなすことにより、力学的エネルギー保存則を利用できます。なお、計算すると以下のようになります。
\(\displaystyle\frac{1}{2}·2mV^2=\displaystyle\frac{1}{2}kx^2\)
\(m×\displaystyle\frac{gh}{2}=\displaystyle\frac{1}{2}kx^2\)
\(x^2=\displaystyle\frac{mgh}{k}\)
\(x=\sqrt{\displaystyle\frac{mgh}{k}}\) (\(x>0\))
こうして、ばねが縮むときの最大距離は\(\sqrt{\displaystyle\frac{mgh}{k}}\)と計算できました。運動量保存則と力学的エネルギー保存則のどちらを利用すればいいのか見極めるようにしましょう。
運動量と力積の概念を学び、運動量保存則を利用できるようにする
物理で力学を学ぶとき、すべての人が運動量と力積の概念を理解しなければいけません。運動の激しさを表すのが運動量であり、力積を利用することによって、2つの物体が衝突する前後での速度変化がわかります。
なお運動量と力積を計算するとき、ベクトルが重要です。物体の方向と力を加える向きが同じである必要があるため、必ずベクトルを意識しましょう。
2つの物体が衝突・合体・分裂するとき、運動量保存則を利用しましょう。作用・反作用による力のみが働いている場合、衝突の前後で運動量の合計は同じです。
なお、運動量保存則と力学的エネルギー保存則の使い分けができるようになりましょう。2つの法則の使い方を理解することにより、物理での計算問題を解けるようになります。






