2つの波が存在する場合、波は互いに強め合ったり弱め合ったりします。この現象を干渉と呼び、物理ではどのようなときに波の干渉が起こるのか学びます。
干渉が起こるときの概念は単純であり、同じ状態の波は強め合い、逆の状態の波は弱め合います。物理では、この現象について式を利用して計算します。
なお教科書に記載されている公式は多くの場合、理解しにくいです。そこで公式がもつ意味を学び、公式を覚えなくても波の干渉条件を導き出せるようにしましょう。事実、公式を覚えても応用問題を解けないため、公式を作れるようにしなければいけません。
2つの波が強め合ったり、弱め合ったりするのは条件があります。そこで、波の干渉条件や問題の解き方を解説していきます。
もくじ
干渉の概念はシンプル:同位相と逆位相
定常波を学んでいる場合、波は互いに強め合ったり弱め合ったりすることを既に理解していると思います。波は独立しており、重ね合わせの原理によって波同士が強め合ったり弱め合ったりするのです。この現象を干渉といいます。
波の山と山(または谷と谷)が重なることで、より大きな山(または谷)が作られます。つまり、同じ状態(同位相)の波では互いに強め合います。一方、山と谷のように逆の状態(逆位相)の波では互いに弱め合います。
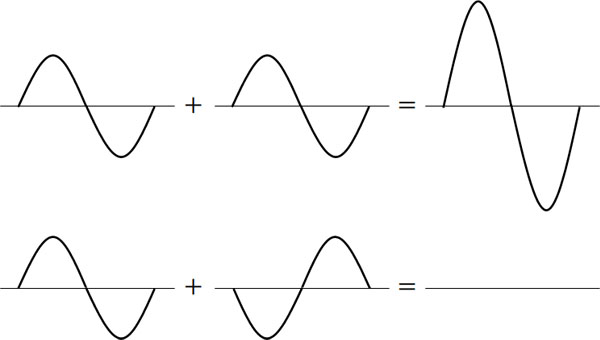
これらの内容を理解すると、干渉の概念は非常にシンプルであるとわかります。
なお位相とは、波の状態を表す言葉です。同じ状態の2つの波では同位相、逆の状態の2つの波では逆位相と呼ばれます。
波の干渉条件を理解するポイント
波が強め合ったり、弱め合ったりする点(場所)は限られます。強め合うには山と山(または谷と谷)が重なる必要があります。一方で波が弱め合うためには、山と谷が重ならなければいけません。
そこで以下の条件を想定し、波の干渉条件を学びましょう。
- 2つの波は同位相でスタートする(波の形は同じ)
- 2つの波は同じ媒質を進む
波の形が違うと、うなりを生じます。そのため理解が難しく、まったく同じ形の波が同位相でスタートする場面を考えましょう。また途中で媒質(空気や水など)が変わると波長が変化するため、同じ媒質を進むと仮定します。
このとき、点Aと点Bから同位相で発せられた波は点Pで強め合うでしょうか、それとも弱め合うでしょうか。

同位相で波が発生されるとき、2つの波は強め合うことがあれば、弱め合うこともあります。そこで、どの場所で波が強め合う(または弱め合う)のか理解するのです。
波の干渉条件の公式:山または谷が重なる点は互いに強め合う
波が強め合うかどうかを確かめるとき、それまで進んだ距離は無視できます。2つの波が一つの点で山と山(または谷と谷)が重なるかどうかが重要だからです。
そこで、点Aから点Pまでの距離(AP)と点Bから点Pまでの距離(BP)について、引き算をしましょう。またAPとBPでどちらの距離が長くなっても問題ないように絶対値を加えましょう。
- \(|AP-BP|\)
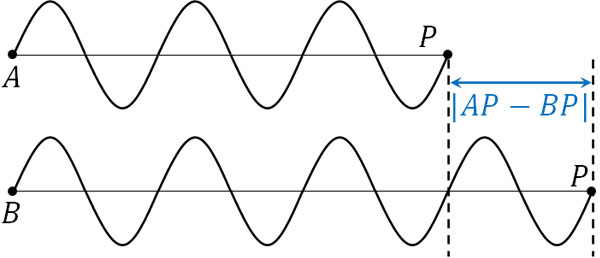
それでは、実際に山と山が重なる場面を考えてみましょう。以下のようにAPとBPの長さが同じ場合、同位相になるため、当然ながら山の部分で重なり合います。
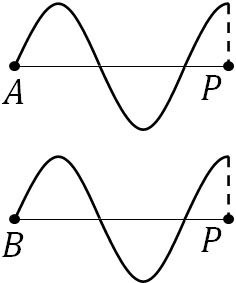
それでは、APの長さが先ほどと同じとして、BPの長さがいくらであれば2つの波は強め合うでしょうか。当然、BPが再び波の山を作れば波Aと波Bは強め合います。例えば以下の場合、2つの波は強め合います。
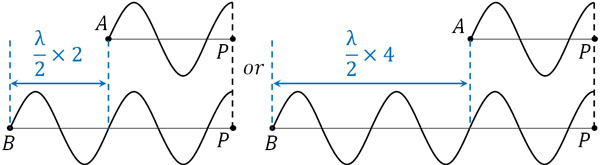
また図より、波長の半分\(\displaystyle\frac{λ}{2}\)を基準にして、偶数倍(0倍、2倍、4倍など)であれば、APとBPの山と山が重なるとわかります。そのため、2つの波が強め合うときの公式は以下になります。
- \(|AP-BP|=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
\(2m\)は必ず偶数になります。そのため、上記の式を利用することによって波が強め合うときの条件を表すことができます。
波が弱め合うときの考え方と公式
次に、波が弱め合うときの公式を確認しましょう。先ほどとは異なり、山と谷が合わさることによって2つの波は互いに打ち消し合います。そのため以下のように、例えばAPの長さで波に山ができ、BPの長さで波に谷ができる場合、2つの波が重なる点Pでは打ち消し合います。
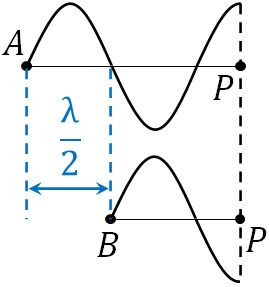
また図より、APとBPの距離の差が波長の半分\(\displaystyle\frac{λ}{2}\)の場合、山と谷が重なることで弱め合うことがわかります。
それでは、BPの長さを変えてみましょう。例えば、以下のようになります。
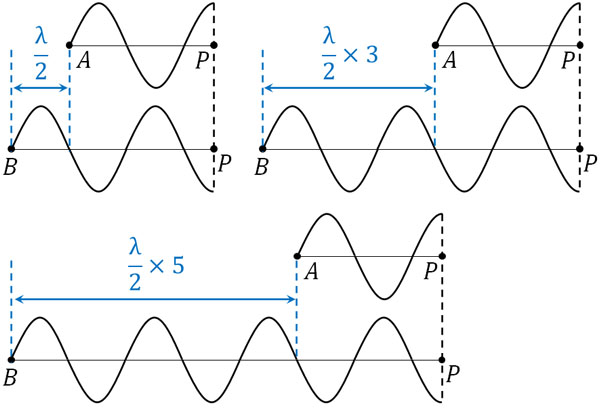
このように、APとBPの差が\(\displaystyle\frac{λ}{2}\)の奇数倍(1倍、3倍、5倍など)であれば、点Pで2つの波が山と谷で重なるとわかります。そこで公式として表すと、以下の場合で2つの波は弱め合います。
- \(|AP-BP|=\displaystyle\frac{λ}{2}×(2m+1)\) (\(m=0,1,2…\))
\(2m+1\)は必ず奇数です。\(\displaystyle\frac{λ}{2}\)と奇数をかければ、2つの波が弱め合う場所がわかります。
教科書に記載されている公式は覚えなくていい
なお物理の教科書によっては、以下のように公式を記していることがあります。
【同位相で強め合う場合】
- \(|AP-BP|=λm\) (\(m=0,1,2…\))
【同位相で弱め合う場合】
- \(|AP-BP|=\left(m+\displaystyle\frac{1}{2}\right)λ\) (\(m=0,1,2…\))
ただ、この公式は絶対に覚えないようにしましょう。その代わりとして、半波長\(\displaystyle\frac{λ}{2}\)を利用し、半波長の偶数倍であれば強め合い、奇数倍では強め合うことを理解しましょう。そうすれば、公式を作ることができます。
\(|AP-BP|=\displaystyle\frac{λ}{2}×2m\) は\(|AP-BP|=λm\)へ変形できます。同様に、\(|AP-BP|=\displaystyle\frac{λ}{2}×(2m+1)\)は\(|AP-BP|=\left(m+\displaystyle\frac{1}{2}\right)λ\)へ変形できます。
そこで教科書に記載されている公式ではなく、\(|AP-BP|=\displaystyle\frac{λ}{2}×2m\) と\(|AP-BP|=\displaystyle\frac{λ}{2}×(2m+1)\)を利用して計算しましょう。
同位相ではなく、逆位相のときは公式が変化する
なぜ教科書に記載されている公式を覚えてはいけないかというと、応用問題が出されると問題を解けないからです。一方で公式の意味を学び、公式を作れるようになれば、すべての応用問題を解けるようになります。
先ほど、点Aと点Bで同位相の波が発生する場面を考えました。それでは、点Aと点Bで逆位相の波が発生する場合、強め合う条件と弱め合う条件はどのようになるのでしょうか。先ほどと異なり、逆位相でスタートする場合の図を作りましょう。
【逆位相で強め合う場合】
2つの波が互いに強め合うためには、山と山(または谷と谷)が重ならなければいけません。そのため、以下のようになります。
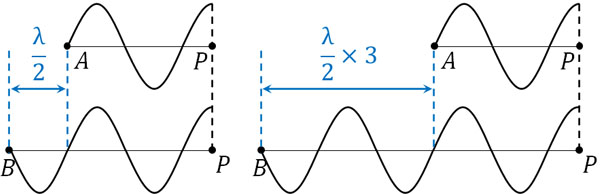
点Aから発生する波と点Bから発生する波の形は逆であり、互いに逆位相の波であるとわかります。この場合、半波長の奇数倍であると2つの波が強め合います。そのため、公式は以下のように変化します。
- \(|AP-BP|=\displaystyle\frac{λ}{2}×(2m+1)\) (\(m=0,1,2…\))
【逆位相で弱め合う場合】
次に逆位相で弱め合う場合の条件を確認しましょう。図にすると以下のようになります。
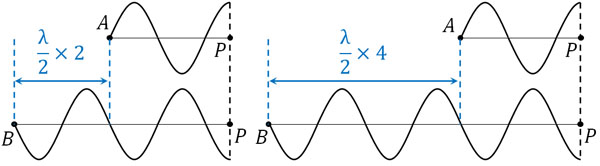
図を確認すると、逆位相の波でスタートする場合、APとBPの距離の差が半波長の偶数倍だと互いに弱め合うことがわかります。そのため、利用する式は以下になります。
- \(|AP-BP|=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
このように、波の条件によって式が変わります。これが、教科書に記載されている公式を暗記しても問題を解けない理由です。そこで公式を暗記するのではなく、なぜ公式が成り立つのか学びましょう。
強め合う点と弱め合う点は規則的に並ぶ
それでは、波の干渉によって強め合っている点または弱め合っている点を結ぶと、どのようになるのでしょうか。
これまで説明した通り、半波長ずれるごとに波は強め合ったり、弱め合ったりします。そこで点Aと点Bから同位相の波が発せられている場面を考えましょう。また理解しやすくするため、点Aと点Bが横軸上に存在するケースで説明します。
2つの点から発せられる波が重なることにより、前述の通り半波長ごとに強め合う部分と弱め合う部分が繰り返されることになります。図にすると以下のようになります。
- \(|AP-BP|=\displaystyle\frac{λ}{2}×n\) (\(n=0,1,2…\))
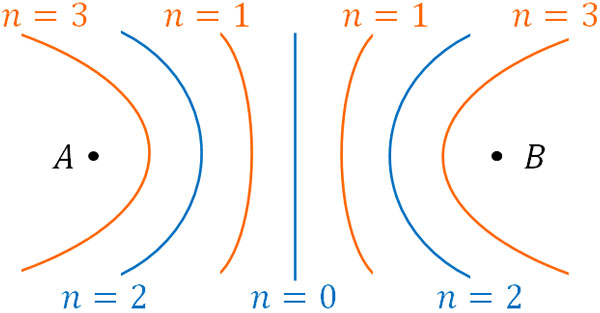
\(|AP-BP|=\displaystyle\frac{λ}{2}×n\)では、\(n\)の値によって半波長の偶数倍になることがあれば、奇数倍になることもあります。\(n\)が偶数の場合、前述の通り波は強め合います。一方で\(n\)が奇数の場合、波は弱め合います。
また図を見てわかる通り、\(|AP-BP|=\displaystyle\frac{λ}{2}×n\)のグラフは双曲線になります。点Aと点Bは2つの点であるため、必ず直線で結ぶことができます。そこでAとBを焦点として双曲線を描けば、どこで波が強め合うのか(または弱め合うのか)がわかります。
なお図ではAとBの間に7本の線があります。ただ何本の線を引けるのかについては、ABの距離と波長に依存します。そのため波の性質によって、AとBの間にある双曲線の数は異なります。
参考までに、逆位相で波が発生される場合、\(n\)が偶数倍であれば波は弱め合い、奇数倍であれば波は強め合います。この現象が起こる理由は既に説明した通りです。
練習問題:波長と位相を確認する
それでは、実際に練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- AとBから逆位相の波が発生しています。波の波長が4cmのとき、下図の点Pで観測される波は強め合っているでしょうか、それとも弱め合っているでしょうか。
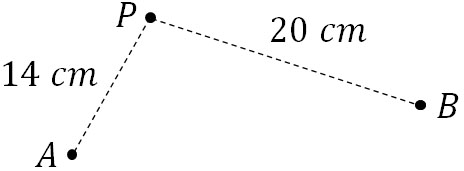
半波長を基準にする必要があり、波長の半分は2cmです。また、\(|AP-BP|=6\)です。そこで、以下の式を作りましょう。
\(|AP-BP|=\displaystyle\frac{λ}{2}×n\)
\(6=2×n\)
\(n=3\)
こうして、半波長を奇数倍できることがわかりました。
重要なのは、AとBから逆位相の波が発生している事実です。この場合、半波長の奇数倍の場所では2つの波が互いに強め合います。こうして、点Pでは波が強め合うと計算できました。
公式の意味を理解し、波の干渉を計算する
波の干渉は概念が簡単です。同じ波の場合は強め合い、逆の波では弱め合います。山と山(または谷と谷)で強め合い、山と谷で弱め合うのです。
ただ波の干渉条件を学ぶとき、公式を覚えてはいけません。また、教科書に記載されている公式を覚えると、応用問題を解くときに利用できないことが多いです。そこで半波長を基準にして、公式を作れるようにしましょう。
また図を描けることも重要です。同位相(または逆位相)の波が発生することにより、どのような場合に波が強め合うのかわかれば、公式を利用しなくても答えを得ることができます。この場合、応用問題であっても問題なく解けます。
波の干渉条件では公式を覚えず、なぜその物理現象が起こるのか原理を理解しましょう。これによって自然現象を理解できるようになり、応用問題を含めて解けるようになります。






