数学で速度の計算をする場合、観測者が静止している状態を基準にして速度計算をします。一方、実際には必ずしも静止している状態とは限りません。例えばあなたが車や電車に乗って移動している場合、静止している状態ではありません。
物理では静止していない状態を想定して計算するケースがひんぱんにあります。そのため静止している状態の速度ではなく、観測者が動いている場合の速度を計算できるようになりましょう。
双方が動いている場合、あなたが感じる速度を相対速度といいます。相対速度を計算することにより、あなたが体感する速度がわかります。
それでは、どのように相対速度を計算すればいいのでしょうか。一直線上でのケースと平面でのケースで相対速度の計算方法が異なります。そこで、具体的な計算方法を確認していきましょう。
もくじ
静止時とは感じる速度が異なる
速度を計算するとき、通常は静止時を想定します。ただ、あなたが動いている場合は体感速度が異なります。
例えば時速60kmで動いている車があるとします。このときあなたが電車に乗っており、車と同じ方向に時速40kmで動いている場合、あなたにとって車のスピードは時速いくらに感じるでしょうか。
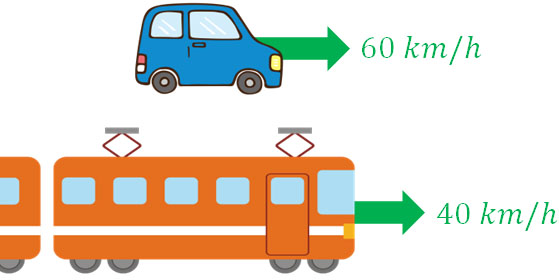
この場合、あなたにとって車の時速は20kmです。\(60-40-20\)により、相対速度を計算できます。
相対速度の公式は覚える必要がない
物理で相対速度を学ぶとき、教科書には相対速度の公式が記されています。あなたが速度\(v_A\)で動いているとき、同じ方向に速度\(v_B\)で動く物体Bの相対速度\(v\)は以下のようになります。
- \(v=v_B-v_A\)
ただ、この公式は意味がないので絶対に覚えないようにしましょう。問題文が変わると、どれが\(v_A\)でどれが\(v_B\)なのかわからないからです。そこで公式を覚えるのではなく、実際にその場面が起こっている状況を想定して、相対速度を計算しましょう。
実際の場面を想定し、相対速度(または相対加速度)を計算する
例えば以下のように、2台の車が反対向きで近づいている場合の相対速度はどのように考えればいいでしょうか。
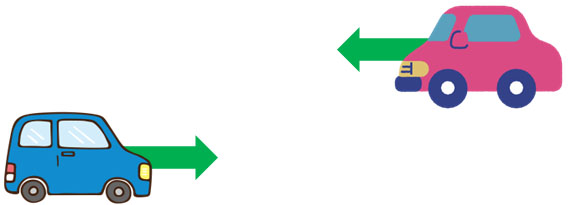
この場合、静止している場面に比べて、相対速度(あなたがどちらか一方の車に乗っている場合の体感速度)は大きくなると誰でも予想できます。そのため、車2台の速度を足せば相対速度を計算できるとわかります。
例えば車が時速30kmであり、もう一方の反対向きで近づいてくる車が時速50kmなのであれば、相対速度は時速80kmです。
他には、あなたが時速60kmの車Aに乗っている場合、同じ方向に向かっている時速50kmの車Bに対する相対速度はいくらでしょうか。
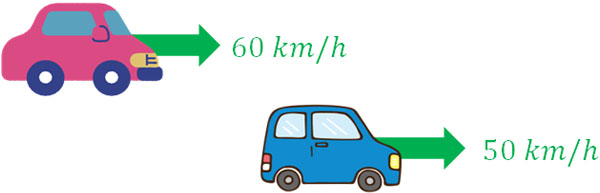
車Aは車Bよりも速度が速いため、あなた(車A)を基準にすると、車Bは時間経過と共に後ろへ下がっていきます。つまり、相対速度(あなたを基準にした車Bの速度)はマイナスでなければいけません。こうして、相対速度は\(50-60=-10\) km/hとわかります。
相対速度の公式を利用する意味はなく、実際に起こる現象を想像しましょう。そうすれば、答えを得ることができます。
なお、同じことは相対速度だけでなく相対加速度にもいえます。あなたを基準として、加速度が増加するのか減少するのかについては、実際に起こっている場面を想像しましょう。
平面上での相対速度の計算
それでは直線上ではなく、平面上での相対速度はどのように計算すればいいのでしょうか。例えば以下のように、一方は東に進み、もう一方は南に進んでいるケースがあります。

この場合、どのように相対速度を計算すればいいのか理解しましょう。例として、Aを基準とするときのBの相対速度を考えましょう。
あなたが車Aに乗って東(右)に進んでおり、車Bが南に向かって進んでいる場合、車Bはどのように動いているように見えるでしょうか。
車A(あなた)は東(右)に進んでいるため、あなたは車Bが左に進んでいるように感じます。また車Bは南に進んでいるため、あなたにとって車Bは南西(左下)へ進んでいます。そのためAを基準とする場合、相対速度\( \overrightarrow{v_{AB}} \)は以下の部分になるとわかります。
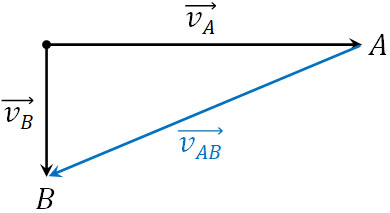
このように実際に起こっている現象を確認すると、どの部分が相対速度に該当するのかわかります。公式を利用しても理解できないため、実際にその現象が起こっている場面を想定し、どの部分が相対速度に当たるのか判断しましょう。
雨の落下速度(相対速度)を計算する
それでは、実際に平面上での相対速度を計算してみましょう。以下の問題の答えは何でしょうか。
- 雨が時速30kmで真下に降っています。あなたが時速30kmで走っている車に乗っている場合、あなたが感じる雨の速度はいくらでしょうか。
例えば、車が東(右)に向かって進んでいるとします。この場合、雨は西(左)に進みます。また雨は真下に降っているため、相対速度の図は以下のようになります。
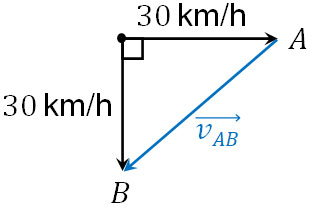
あなたが車に乗っており、東(右)に進んでいる場合、窓から見える雨の向きは左下であると想像できます。そのため、この図に間違いはないとわかります。物理では、実際にその現象が発生している場面を想定しましょう。
また図を確認すると、直角二等辺三角形となっています。そのため、\( \overrightarrow{AB} \)は\(30\sqrt{2}\) km/hとわかります。こうして、相対速度を求めることができました。
公式を利用せず、実際の現象を観察する
物理では、公式を覚えないほうが効率的に問題を解ける場面が多いです。その一つが相対速度であり、公式を利用する人ほど計算ミスをします。
相対速度で符号のプラスやマイナスを判断するとき、実際に起こっている現象を想像しましょう。あなたを基準にするとき、物体が遠ざかっている場合、相対速度はプラスです。一方、物体があなたに近づいている場合、相対速度はマイナスです。
また相対速度の計算が足し算になるのか、それとも引き算になるのかについても、実際の現象を想像すれば容易に判断できます。
それに加えて、平面上での相対速度も計算できるようになりましょう。平面ではベクトルで考えます。このときも実際の現象から、相対速度の向きを判断するといいです。公式を利用しないのが相対速度の問題を解くコツです。






