静止している物体は必ず力のつり合いが取れています。つまり、同じ力によって引っ張り合っています。もし力のつり合いがない場合、物体は動きます。
そこで物理で力学を学ぶとき、どのように力のつり合いが働くのか理解しなければいけません。力の単位にニュートンがあり、ニュートンが何を意味しているのか学びましょう。また、物体に働く力を見つけられるようになりましょう。
なお力のつり合いを理解するためには、ほかにも作用・反作用の法則を学ばなければいけません。また、力を水平方向と垂直方向に分けることも重要です。
力のつり合いでは、糸の張力や滑車を利用する問題がひんぱんに出されます。そこで、どのように物理でこれらの問題を解けばいいのか解説していきます。
もくじ
静止状態での力のつり合い
すべての静止している物体では力がつり合っています。力がつり合っているというのは、力の合計が0であることを意味しています。
力のつり合いが取れていない場合、必ず物体は動きます。言い換えると、加速度を生じます。例えば以下の状態では、物体は動くでしょうか、それとも静止しているでしょうか。
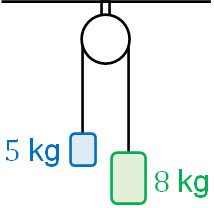
この場合、物体は静止しておらず動くと容易に想像できます。5kgよりも8kgのほうが重いため、物体は静止していません。静止していない状態というのは、このように力の大きさが異なっています。また、加速度を生じることによって時間経過と共に物体が動くスピードは速くなります。
一方、2つの物体の重さが同じ場合、静止します。この場合は力のつり合いが取れており、加速度はゼロです。すべての力を合わせるとゼロになる場合、力がつりあっており、物体は静止するのです。
力の単位:ニュートン(N)は重さと加速度をかける
物理で重要な力には複数の種類があります。その中でも、力学で最初に学ぶのが重力と接触力です。接触力には、垂直抗力や張力、ばねの弾性力、摩擦力など多くの種類があります。つまり、物体と接触する部分で働く力が接触力です。
他にも慣性力や電気的な力などの種類はあるものの、力学で力のつり合いを学ぶとき、重力と接触力だけで考えましょう。
このとき、力の単位はニュートン(N)です。1kgの物体に1m/s2の加速度が加わっている場合、1Nと定義されています。つまり力の単位は物体の重さと加速度のかけ算によって得られます。
例えば体重100kgの人では、重力加速度が9.8m/s2であるため、980Nの力で常に地面(地球)を押していることになります。
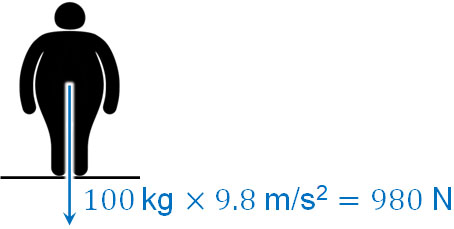
なお力学で力を表すとき、矢印を利用します。また物理ではベクトルが重要であり、矢印によって力が働く方向を記しましょう。例えば重力の場合、必ず下向きの力が働きます。すべての物体は地球に引っ張られているため、重力を表すときはすべてのケースにおいて下向きです。
ひもが引っ張る力の計算方法
それでは、実際に力のつり合いが取れている場面で力の大きさを計算してみましょう。以下の問題の答えは何でしょうか。
- 質量\(m\)の重りが天井から糸でつるされています。重力加速度を\(g\)とするとき、糸が重りを引っ張る力(張力\(T\))を求めましょう。
まず、以下の図を作ります。
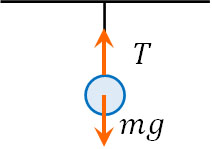
すべての物体には重力が働きます。球の重さは\(m\)であるため、重力加速度\(g\)をかけることで、重力による力は\(mg\)とわかります。
なお、球は静止しています。つまり、\(mg\)(重力による力)と同じ力で引っ張られているとわかります。
また物理ではベクトルを考慮する必要があり、すべてのベクトルを足して0になることで力のつり合いが取れます。球は糸で引っ張られているため、重力と反対向きの力で引っ張れば、球が静止するとわかります。
前述の通り、球に働く重力は\(mg\)です。そこで糸による張力\(T\)と重力\(mg\)が同じであれば、球は静止します。つまり\(T=mg\)であれば力のつり合いが取れることになり、糸が重りを引っ張る力は\(mg\) Nとわかります。
物体に働く力の見つけ方とベクトルの向き
先ほど、物体(球)に働く力を図示しました。ただ実際の問題では、あなたが図に力を記入して問題を解かなければいけません。どのようにして、物体に働く力を見つければいいのでしょうか。
物体に働く力の見つけ方は単純であり、一つの物体に着目した後、以下の操作をしましょう。
- 物体と接触している部分に対して力(ベクトル)を記す
- 重力によるベクトルを記す
一つの物体に対して、接触している部分は必ず何らかの接触力が働きます。そのため接触している部分には、必ず力(ベクトル)を記載しましょう。例えば以下の図で箱Aに着目する場合、以下の部分で接触しています。
- 箱Aと床
- 箱Aと指
- 箱Aとひも
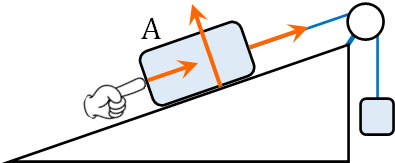
重要なのは、着目している物体が受ける力のみを記載することがあります。着目している物体が与える力ではありません。このポイントを理解すれば、ベクトルの向きがわかります。
箱Aに着目する場合、床は箱Aを下から上に押し上げています。また、ひもは箱Aを引っ張っています。指は箱Aを押しています。静止状態ではあっても、箱Aには3つの力が加わっているとわかります。
最後に、重力を加えましょう。箱Aと接している部分にベクトルを加えた後、以下のように箱Aの中心から真下に重力を記すことによって、物体に働くすべての力を図示できるようになります。
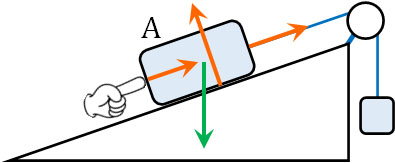
なお着目する物体が違うと、働く力も変わります。例えばひもを利用して天井から重りをつるす場合、着目する物体によって以下のようにベクトルが変化します。

球に着目する場合、球はひもと接触しています。そのため、ひもによる張力と重力を記載します。
一方でひもに着目する場合、ひとは球と天井に触れています。球はひもを下に引っ張り、天井はひもを上に引っ張っています。なおひもには重力が加わっているものの、ひもは軽く、球に比べて重さを無視できます。そのため、ひもに着目するケースでは例外的に重力を加えていません。
また天井に着目する場合、天井はひもと接触しています。また天井には重力が加わっています。ひもは天井を下に引っ張り、さらには重力によって天井は下に引っ張られています。
ただ天井は静止しているため、どこかに天井を上に押し上げる力が働かなければいけません。天井があるというのは、柱と接していることを意味します。そのため、天井は柱によって上に押し上げられています。こうして、天井は力のつり合いによって静止しています。
力学の問題を解くとき、着目する物体を決めましょう。その後、着目する物体と接している部分に対してベクトルを記載します。反対に、接していない部分で接触力が働くことはありません。また着目する物体が受ける力を記載することで、ベクトルの向きがわかります。
作用・反作用の法則で力の向きと大きさを探す
ここまで、物体に働く力を解説してきました。それでは、物体に働く力の大きさはどのように考えればいいのでしょうか。このとき重要な法則に作用・反作用の法則があります。
前述の通り、静止するためには物体に働く力がつりあっている必要があります。そのため特定の力で押し、さらには静止している場合、反対方向の力で押されていることを意味します。
例えば体重100kgの人であれば、980Nの力で地面(地球)を押しています。同時に、地面は人を980Nで押し上げています。

力を加える場合、静止しているのであれば、必ず反対方向の同じ力が加わっていると考えましょう。これを作用・反作用の法則といいます。例えば、以下の問題の答えは何でしょうか。
- 10kgの箱に糸をつけて引っ張ります。糸の張力が2kgであり、重力加速度が\(g\)のとき、床から箱への垂直抗力はいくらですか。
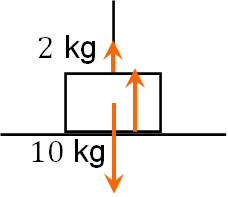
箱が床を押す力(重力)は\(10g\)です。そのため作用・反作用の法則により、重量以外に力が働いていないのであれば、上方向に\(10g\)の力で押し返されていることになります。
ただ糸の張力が\(2g\)であるため、垂直抗力の計算では\(10g\)から\(2g\)を引かなければいけません。そのため、答えは\(8g\) Nです。
力を水平方向と鉛直方向に分解する
なお力のつり合いについて、ベクトルが直線方向ではなく、異なる方向に向いていることがあります。この場合、水平方向の力と鉛直方向の力に分解しましょう。物理では力を分解することがひんぱんにあります。
物体が静止している場合、水平方向と鉛直方向の力を足すと必ずゼロになります。ゼロでない場合、物体は加速度を伴って動かなければいけません。静止しているというのは、すべての力の合計がゼロであることを意味しています。
それでは、実際に力を水平方向と鉛直方向に分解して物理の問題を解いてみましょう。
- 以下の図について、糸1の張力\(T_1\)と糸2の張力\(T_2\)はそれぞれいくらでしょうか。なお球の重さは10kgであり、重力加速度は\(g\)です。
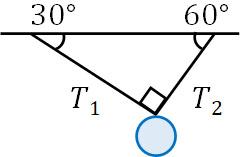
この問題を解くため、球に着目して力を書き加えましょう。

球は静止しているため、全体の力はつり合っています。ただ張力\(T_1\)と張力\(T_2\)はベクトルの向きが異なります。そこで、力を水平方向と鉛直方向に分解しましょう。力を分解すると、それぞれ以下のようになります。
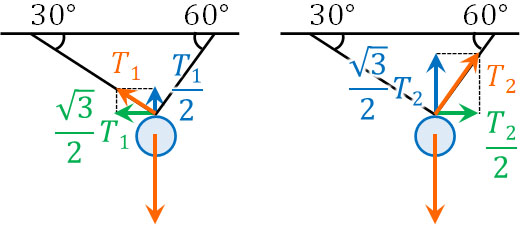
物体は静止しているため、水平方向の力はつり合っています。そのため、以下の関係が成り立ちます。
\(\displaystyle\frac{\sqrt{3}}{2}T_1=\displaystyle\frac{1}{2}T_2\)
\(\sqrt{3}T_1=T_2\)
こうして、張力\(T_1\)と張力\(T_2\)の力の大小関係がわかりました。
次に鉛直方向の力のつり合いを確認しましょう。球による重力と糸による張力はつり合っています。そのため、以下の関係が成り立ちます。
\(10g=\displaystyle\frac{1}{2}T_1+\displaystyle\frac{\sqrt{3}}{2}T_2\)
そこで、\(\sqrt{3}T_1=T_2\)を代入しましょう。
\(10g=\displaystyle\frac{1}{2}T_1+\displaystyle\frac{3}{2}T_1\)
\(10g=2T_1\)
\(T_1=5g\)
こうして、\(T_1\)の張力は\(5g\) Nとわかりました。また\(\sqrt{3}T_1=T_2\)なので、\(T_2\)の張力は\(5\sqrt{3}g\) Nです。
・力の分解は水平方向と鉛直方向とは限らない
わかりやすく説明するため、力の分解を水平方向と垂直方向で考えました。ただ、力を分解するときは必ずしも水平方向と鉛直方向ではないことを理解しましょう。例えば、以下のケースがあります。
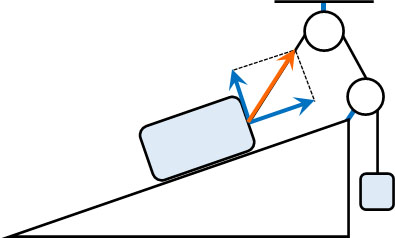
この場合、力を分解した後のベクトルは水平方向や鉛直方向ではありません。ただ、このように力を分解することによって力のつり合いを確認できます。
滑車とつり合いの練習問題
それでは、応用問題を解いてみましょう。一つの物体について力のつり合いを考えるのではなく、二つの物体での力のつり合いを考えることで計算するのです。以下の問題の答えは何でしょうか。
- 以下の図のように、10kgの板に50kgの人が乗っています。人が定滑車のひとも引っ張り、静止しています。ひもの質量と摩擦を無視でき、重力加速度を\(g\)とします。
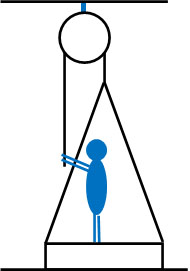
- 板が地面から離れるとき、どれだけの力でひもを引っ張ればいいでしょうか。
- 重さを無視できる体重計に人が乗っている場合、板が地面から離れるときに体重計は何kgを示しますか。
1) 板が地面から離れるとき、どれだけの力でひもを引っ張ればいいでしょうか
まず、人と板にわけて力のつり合いを考えましょう。以下のように力を分け、人と板に着目して力のベクトルを図示しましょう。
- T:人がひもを引っ張る力(ひもの張力)
- N:人が板から受ける垂直抗力(板が人から受ける力)
- R:板が地面から受ける垂直抗力
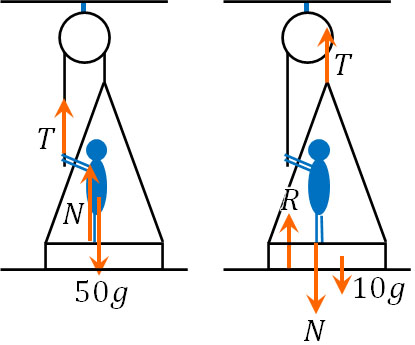
人に着目する場合、ひもと板に接しています。そのため、人に着目するときの接触力は2つでえす。さらに、人に加わる重力を加えましょう。そのため、人に着目するときの力のつり合いは以下のようになります。
\(T+N=50g\)
次に板(ゴンドラ)に着目します。この場合、板(ゴンドラ)はひも、地面、人と接しています。そのため、板が受ける接触力は3つです。これに重力を加えると、力のつり合いは以下のようになります。
\(T+R=10g+N\)
板が地面から離れるとき、当然ながら\(R=0\)となります。そこで\(R=0\)を代入すると、\(T=10g+N\)となります。そこで、\(T=10g+N\)を\(T+N=50g\)に代入しましょう。
\(T+N=50g\)
\(10g+N+N=50g\)
\(2N=40g\)
\(N=20g\)
\(N=20g\)とわかったため、\(T=30g\)と計算できます。つまり、\(30g\) Nの力で引っ張れば板は地面から離れます。
2) 重さを無視できる体重計に人が乗っている場合、板が地面から離れるときに体重計は何kgを示しますか
人の体重は50kgであるものの、張力\(T\)で引っ張っているため、その分だけ体重計が示す重さは軽くなります。言い換えると、\(N\)を確認することで体重計が示す重さがわかります。板(体重計)が人から受ける力が\(N\)だからです。
先ほどの計算より、\(N\)の力の大きさは\(20g\) Nです。力は重さと加速度のかけ算によって得られるため\(g\)で割ると、20kgを得られます。つまり、体重計が示す重さは20kgです。
物体に働く力とベクトルを理解する
物体が静止しているとき、すべての力を足すと必ずゼロになります。加速度がゼロである場合、力がつりあっているのです。
そこで、力の大きさと向き(ベクトル)を図に記入できるようになりましょう。一つの物体に着目し、接している部分と重力を書き加えると、物体に働く力を図示できるようになります。
このとき重要な法則に作用・反作用の法則があります。物体が静止している場合、力を加えると反対方向の力が生まれます。また力の向きが異なる場合、力を水平方向と鉛直方向に分解しなければいけないケースもあることを学びましょう。
力学は住宅建築や機械設計(エレベーター、クレーン)など、多くの場面で利用されています。力のつり合いは力学の基礎であるため、どのように力を図示すればいいのか理解しましょう。






