定積変化・定圧変化：定積モル比熱・定圧モル比熱とマイヤーの関係式

気体の状態変化では、気体の体積や圧力、温度が変化する場面を学びます。気体から液体など、物質の形が変化するときだけでなく、気体の環境が変化するときも気体の状態変化が利用されます。

そこで気体の状態変化の中でも、定積変化と定圧変化を学びましょう。体積が一定の場合、気体による仕事はゼロになります。また圧力が一定の場合、気体の状態方程式を利用して計算することができます。

また定積変化と定圧変化を学べば、定積モル比熱と定圧モル比熱の公式を導出できます。簡単に公式を得ることができるため、公式を覚えるのではなく、公式の導き出し方を理解しましょう。

それでは、定積変化や定圧変化の特徴には何があるのでしょうか。それぞれの状態変化について、熱力学第一法則を利用して性質を学びましょう。

1 体積が一定の場合、気体による仕事はゼロ
- 1.1 定積変化での公式と\(P-V\)グラフ
2 定圧変化では、気体が行う仕事は\(PΔV\)となる
- 2.1 熱力学第一法則と定圧変化の関係：状態方程式の利用
- 2.2 定圧変化での\(P-V\)グラフ
3 比熱とモル比熱の関係
4 定積変化と定圧変化の関係を理解する

体積が一定の場合、気体による仕事はゼロ

気体の状態変化で特殊なケースを想定しましょう。まず、体積が一定の場合を考えます。体積を一定に保ち、熱量を加える場合はどのような変化が起こるでしょうか。

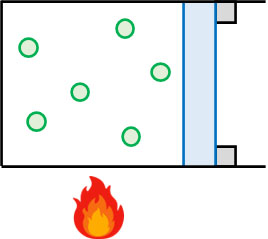
熱力学第一法則より、以下の公式が成り立ちます。

\(Q=ΔU+W\)

また、気体による仕事は\(W=PΔV\)で表すことができます。定積変化では、体積の変化量\(ΔV\)はゼロです。そのため、気体が行う仕事\(W\)はゼロです。そこで熱力学第一法則に\(W=0\)を代入すると、公式は以下のように変わります。

\(Q=ΔU\)

内部エネルギー\(U\)は気体の温度（運動エネルギー）を表します。そのため\(Q=ΔU\)というのは、熱量を加えるとすべて温度上昇に利用されることを意味します。

定積変化での公式と\(P-V\)グラフ

内部エネルギーの公式は\(U=\displaystyle\frac{3}{2}nRT\)です。また、内部エネルギーの変化量\(ΔU\)は温度変化\(ΔT\)を利用して以下のように表すことができます。

\(ΔU=\displaystyle\frac{3}{2}nRΔT\)

前述の通り定積変化では、加えた熱量はすべて内部エネルギー（温度）の上昇に利用されます。そのため熱力学第一法則より、定積変化では加えた熱量を以下のように表すこともできます。

\(Q=\displaystyle\frac{3}{2}nRΔT\)

\(ΔU\)を\(\displaystyle\frac{3}{2}nRΔT\)に変えただけなので、この関係が成り立つのは容易に理解できると思います。

・定積変化と\(P-V\)グラフ

それでは、定積変化するときの\(P-V\)グラフはどのようになるのでしょうか。横軸（体積）の変化はないため、たて軸（圧力）のみ変化することになります。そのため熱量\(Q\)を加える場合、\(P-V\)グラフは以下のように変化します。

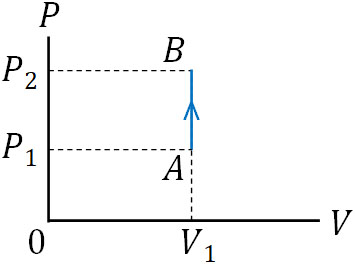
温度が上昇するとき、通常だと気体の体積は膨張します。ただ体積は一定であるため、温度上昇によって圧力が上がります。反対に温度を下げると、容器内の圧力は下がります。

なおボイル・シャルルの法則より、\(\displaystyle\frac{PV}{T}\)は一定です。定積変化では体積\(V\)に変化がないため、\(\displaystyle\frac{P}{T}\)は一定です。そのため、以下の式を作れます。

\(\displaystyle\frac{P}{T}=a\) （\(a\)は定数）
\(P=aT\) （\(a\)は定数）

式を確認すると、定積変化では圧力\(P\)と温度\(T\)が比例の関係になっているとわかります。そのため温度が2倍になれば、圧力は2倍になります。一方で温度が\(\displaystyle\frac{1}{3}\)になれば、圧力も\(\displaystyle\frac{1}{3}\)になります。

定圧変化では、気体が行う仕事は\(PΔV\)となる

次に定圧変化での計算方法を解説していきます。常に圧力が一定で気体の状態変化が起こる場合、定圧変化となります。

ピストンが自由に動く場合、シリンダー内の圧力は常に一定になります。シリンダー内の圧力は大気圧と同じになるからです。

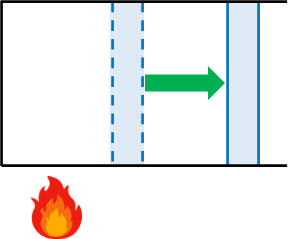
定圧変化で重要なのは、\(W=PΔV\)の公式を使えることです。圧力が一定でない場合、\(W=PΔV\)は成り立ちません。一方で定圧変化では\(W=PΔV\)を利用できるため、体積の増減によって仕事\(W\)を計算できます。

そこで熱力学第一法則の公式を\(W\)から\(PΔV\)に変えましょう。以下のようになります。

\(Q=ΔU+PΔV\)

気体による仕事を利用することにより、定圧変化で使用できる公式を得ることができました。

熱力学第一法則と定圧変化の関係：状態方程式の利用

なお定圧変化では、体積が増えることによって温度も上昇します。気体の状態方程式より、\(PV=nRT\)です。また\(ΔV\)の体積上昇による温度上昇が\(ΔT\)のとき、変化前の温度は\(T\)であり、変化後の温度は\(T+ΔT\)です。

変化量を計算するとき、後から前を引きましょう。そのため、以下の式を作ることができます。

\(PΔV=nR(T+ΔT)-nRT\)

\(PΔV=nRΔT\)

つまり定圧変化で体積が\(ΔV\)増えるとき、それに比例して温度は\(ΔT\)増えます。また体積が\(ΔV\)減る場合、それに比例して温度は\(ΔT\)減ります。そのため、定圧変化では熱力学第一法則を以下のように変形することもできます。

\(Q=ΔU+nRΔT\)

定圧変化では、\(PΔV=nRΔT\)となることを理解しましょう。

・定圧変化では\(Q=\displaystyle\frac{5}{2}nRΔT\)となる

なお内部エネルギーの公式より、\(ΔU=\displaystyle\frac{3}{2}nRΔT\)です。そのため定圧変化では、以下のように公式を変形できます。

\(Q=ΔU+nRΔT\)

\(Q=\displaystyle\frac{3}{2}nRΔT+nRΔT\)

\(Q=\displaystyle\frac{5}{2}nRΔT\)

定圧変化では、加えた熱量を物質量と温度変化のみで計算することができます。

定圧変化での\(P-V\)グラフ

それでは、定圧変化での\(P-V\)グラフはどのような形になるのでしょうか。定圧変化では圧力が一定であるため、たて軸の値は変化しません。横軸（体積）の値のみ変化します。そのため、\(P-V\)グラフは以下のようになります。

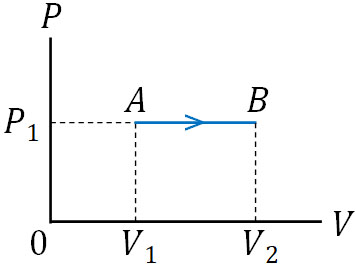
定圧変化で正の方向に値が上昇するとき、「気体は仕事を行い、温度が上昇した」と考えることができます。前述の通りボイル・シャルルの法則により、定圧変化では温度が上昇すると、それに比例して体積が上昇します。

一方、定圧変化で体積が減っている場合、「気体は外部から仕事をされ、温度が下降した」と捉えることができます。

比熱とモル比熱の関係

定積変化でも定圧変化でも、加えた熱量を温度変化の式のみで表現することができます。そこで、比熱を用いてこれらの関係を表しましょう。

物体1gを1K（1℃）上昇させるために必要な熱量が比熱です。質量をそろえることによって、物体の温まりやすさを表すのです。

それでは固体や液体ではなく、気体についてはどのように比熱を表せばいいのでしょうか。気体の場合、1gを測定するのは困難です。そこで気体では、質量ではなく物質量を基準にしましょう。物質量を用いる比熱をモル比熱といいます。具体的には、1molの気体を1K上昇させるために必要な熱量がモル比熱です。

比熱では、\(c\)を用いて以下の公式を利用します。

\(Q=mcΔT\)

一方でモル比熱では、質量\(m\)ではなく、物質量\(n\)を利用します。そこでモル比熱を\(C\)とすると、公式は以下になります。

\(Q=nCΔT\)

モル比熱\(C\)は定数であり、気体の種類によって変化します。また前述の通り、モル比熱は1molの気体の温度を1K上昇させるために必要な熱量を指します。そのためモル比熱に物質量と温度変化をかけると、熱量を得られるのは当然です。

モル比熱の定義を理解すれば、公式を覚えなくても式を作ることができます。

なおモル比熱には、定積モル比熱と定圧モル比熱があります。定積変化と定圧変化では、モル比熱の計算方法が異なります。そこで、それぞれのモル比熱を計算できるようになりましょう。

定積モル比熱を計算する

先ほど説明した通り、定積変化では\(Q=ΔU\)となります。定積変化では気体による仕事がないため、\(W=0\)です。熱を加える場合、すべて内部エネルギーの上昇に利用されます。

また\(ΔU=\displaystyle\frac{3}{2}nRΔT\)であるため、定積変化では以下の公式に変換することができます。

\(Q=\displaystyle\frac{3}{2}nRΔT\)

そこで、\(Q=nCΔT\)と比べてみましょう。定積変化でのモル比熱を\(C_V\)とすると、\(C_V=\displaystyle\frac{3}{2}R\)であれば、モル比熱の式に変換できるとわかります。\(Q=\displaystyle\frac{3}{2}nRΔT\)に\(C_V=\displaystyle\frac{3}{2}R\)を代入すれば、\(Q=nC_VΔT\)となります。

\(C_V=\displaystyle\frac{3}{2}R\)

なお\(C_V=\displaystyle\frac{3}{2}R\)であるため、理想気体である単原子分子では、定積モル比熱は気体定数だけで決まります。気体の種類に関係なく、定積モル比熱が決定されるのです。

定圧モル比熱の値も気体定数で決まる

同じように、定圧変化での気体のモル比熱を計算しましょう。定圧モル比熱を\(C_P\)とします。前述の通り、気体の熱量は以下の公式で表すことができます。

\(Q=\displaystyle\frac{5}{2}nRΔT\)

そこで、先ほどと同様に\(Q=nCΔT\)と比べてみましょう。\(Q=\displaystyle\frac{5}{2}nRΔT\)から\(Q=nCΔT\)を作るためには、定圧変化での気体のモル比熱が\(C_P=\displaystyle\frac{5}{2}R\)であればいいとわかります。\(Q=\displaystyle\frac{5}{2}nRΔT\)に\(C_P=\displaystyle\frac{5}{2}R\)を代入すれば、\(Q=nC_PΔT\)となります。