水平投射・斜方投射：物理でのベクトルとモンキーハンティング

物理を学ぶとき、多くの人が混乱する内容に水平投射と斜方投射があります。物理では水平方向と垂直方向に分けて動きを考える必要があります。また世の中の現象には、直感とは反する現象もひんぱんに存在します。その一つが水平投射です。

水平投射と斜方投射は直線運動ではなく、平面運動です。そこで、平面で動く物体の運動を理解しましょう。

なお斜方投射の応用問題としてモンキーハンティングがあります。水平投射や斜方投射に比べて内容は難しくなるものの、解き方や考え方は同じです。

それでは、どのように水平投射と斜方投射を考えればいいのでしょうか。高校物理で学ぶ水平投射と斜方投射を解説していきます。

1 水平投射では、水平方向と鉛直方向で運動を分解する
2 斜方投射では鉛直方向で初速度\(v_0\)が加わる
- 2.1 斜方投射に関わる練習問題
3 モンキーハンティング：空中での2物体の衝突
4 水平投射と斜方投射の考え方を学ぶ

水平投射では、水平方向と鉛直方向で運動を分解する

自由落下や鉛直投げ下げは直線上での運動です。一方で水平投射では、平面での運動になります。以下のように物体を真横に投げるときの運動が水平投射です。

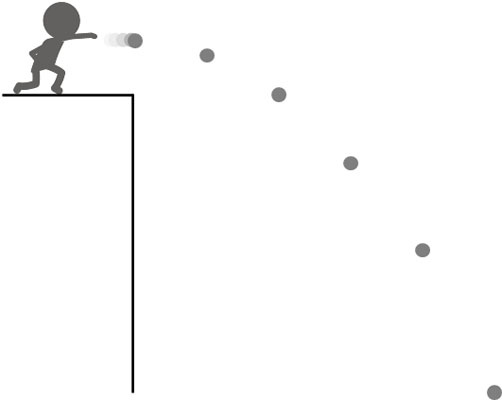
水平投射がどのような動きをするのか予想するのは簡単です。水平投射では、物体は横へ移動します。また、時間経過と共に落下スピードは速くなります。水平投射を学ぶとき、物体が実際に落下する場面を思い浮かべましょう。

水平投射では、物体は曲線を描くため、このままでは計算が難しいです。そこで、水平方向と鉛直方向に動きを分けましょう。物理ではベクトル（成分）ごとに分けて考えるケースが多く、これによって平面での物体の動きを把握できるのです。

水平方向の速さは一定であり、鉛直方向は自由落下と同じ

平面での物体の動きを考えるとき、水平方向と鉛直方向に分けましょう。図では以下のようになります。

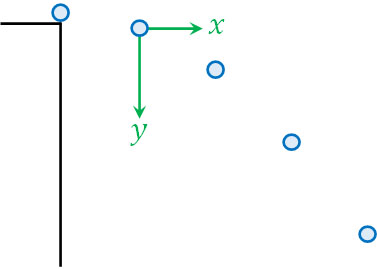
それでは、水平方向と鉛直方向に働く力は何でしょうか。

・水平方向：加わる力はなく、等速直線運動となる

物体を真横に投げた後、水平方向に加わる力は何もありません。そのため、水平方向では等速直線運動となります。つまり、同じ速度で水平方向へ移動します。

・鉛直方向：重力により、自由落下と同じになる

それに対して、鉛直方向では重力のみが加わります。つまり重力による加速度\(g\)が下向きに働くのです。

水平投射では、真横に物体を投げます。このとき鉛直方向で考えると、下向きの初速度\(v_0\)は0です。また重力加速度のみが加わるため、水平投射での鉛直方向というのは自由落下と同じです。

なぜ鉛直方向は自由落下と同じで考えるのか

水平投射では鉛直方向を自由落下として考えるため、実際に自由落下させる場合と水平投射を行う場合を比べると、地面に到着する時間は同じです。

例えば物体Aを自由落下させ、物体Bを水平投射させます。この場合、時間経過と共に、以下のように物体の動きが変化します。

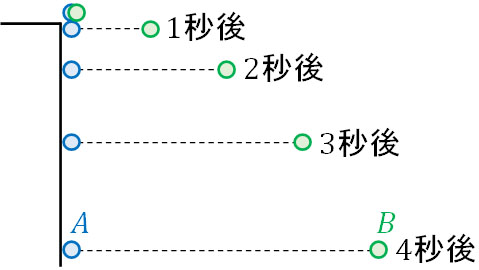
それでは、なぜ物体Aと物体Bは同時に地面に到着するのでしょうか。水平方向を加味すると、物体Bのほうが移動距離は長いため、物体Aと物体Bが同時に地面に到着するのは変に思えてしまいます。

物体Bは曲線にて移動しているものの、成分（ベクトル）で分けることで鉛直方向のみを取り出せば、直線運動をしています。物体Bに対して鉛直方向に加わる力（重力）は、物体Aへ下向きに加わる力と同じです。当然、重力に変化はありません。

例えば、物体Bと同じスピードであなたが水平移動する場面を考えましょう。

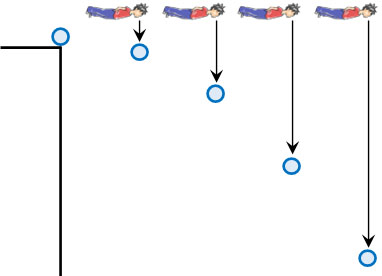
この場合、物体と同じスピードで横に移動しているあなたにとって、物体Bの水平方向への移動は0です。つまり、あなたを基準にすると物体は自由落下しています。当然、人が平行移動しているかどうかに関係なく、鉛直方向に働く力（重力）は常に一定であるため、自由落下と水平投射では同時に地面に到着します。

水平投射の計算問題

水平投射を理解するため、実際に問題を解いてみましょう。以下の問題の答えは何でしょうか。

高さ\(h\)のビルの上から水平方向に速度\(v’\)でボールを投げました。なお、重力加速度は\(g\)です。

ボールが地面に到着するまでの時間はいくらですか。
ボールが地面に到着するとき、水平方向ではどれだけ移動しますか。
ボールが地面に到着する直前の速さ\(v\)と地面との角度をθとするとき、tanθはいくらですか。
ボールが地面に到着する直前の速度\(v\)はいくらですか。

1) ボールが地面に到着するまでの時間はいくらですか

水平投射では、鉛直方向は自由落下と同じです。そのため自由落下と同様に計算しましょう。

\(x=v_0t+\displaystyle\frac{1}{2}at^2\)

\(h=\displaystyle\frac{1}{2}gt^2\)

\(t^2=\displaystyle\frac{2h}{g}\)

\(t=\sqrt{\displaystyle\frac{2h}{g}}\) \((t>0)\)

こうして、\(\sqrt{\displaystyle\frac{2h}{g}}\)秒後に地面にボールが到着するとわかります。

2) ボールが地面に到着するとき、水平方向ではどれだけ移動しますか

水平方向では、速度は常に\(v’\)です。また\(\sqrt{\displaystyle\frac{2h}{g}}\)秒後に地面がボールに到着することから、水平方向での移動距離は\(v’\sqrt{\displaystyle\frac{2h}{g}}\)です。

3) ボールが地面に到着する直前の速さ\(v\)と地面との角度をθとするとき、tanθはいくらですか。

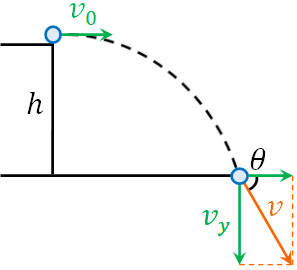
まず、ボールが地面に到着する直前の鉛直方向の速さ\(v_y\)を計算しましょう。

\(v=v_0+at\)

\(v_y=0+g\sqrt{\displaystyle\frac{2h}{g}}\)

\(v_y=\sqrt{2gh}\)

鉛直方向の速さは\(v_y=\sqrt{2gh}\)であり、水平方向の速さは\(v’\)です。そのため、tanθは以下のようになります。

\(tanθ=\displaystyle\frac{\sqrt{2gh}}{v’}\)

4) ボールが地面に到着する直前の速度\(v\)はいくらですか

ボールの速さは三平方の定理を利用することによって計算しましょう。鉛直方向の速さは\(v_y=\sqrt{2gh}\)であり、水平方向の速さは\(v’\)です。そのため、以下のように計算できます。

\(v^2=v_y^2+v’^2\)

\(v^2=2gh+v’^2\)

\(v=\sqrt{2gh+v’^2}\) （\(v>0\)）

こうして、ボールが地面に到着する直前の速さは\(\sqrt{2gh+v’^2}\)と計算できました。

斜方投射では鉛直方向で初速度\(v_0\)が加わる

水平投射を学べば、斜方投射を理解するのは簡単です。水平投射の場合、鉛直方向は自由落下になります。一方で斜方投射では、鉛直方向は鉛直投げ上げとなります。斜め上にボールを投げるのが斜方投射になるからです。

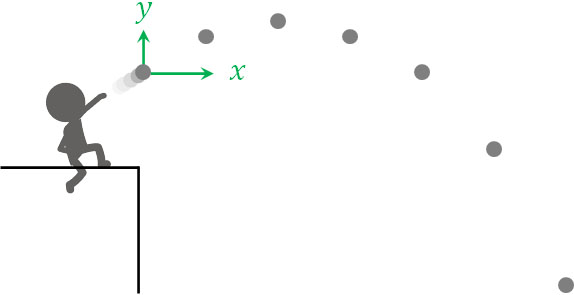
ただ水平投射とは異なり、斜方投射では斜め上に投げることになるため、水平方向の力と鉛直方向の力をそれぞれ計算しなければいけません。

計算方法は簡単であり、三角比を学んでいる場合は容易に計算できます。初速度\(v_0\)で投げ、地面との角度をθとするとき、水平方向の力と鉛直方向の速度はそれぞれ以下のようになります。

水平方向の力：\(v_0cosθ\)
鉛直方向の力：\(v_0sinθ\)

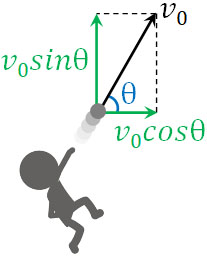
数学で三角比を学んでいる場合、問題なく理解できると思います。平面での運動ではベクトル（成分）によって分ける必要があるため、sinθとcosθを利用することで速度を分けるのです。

斜方投射に関するその他の考え方はこれまで説明した内容と同じです。なお鉛直方向は速度の向きと重力加速度の向きが逆であるため、重力加速度が\(-g\)になることに注意しましょう。

斜方投射に関わる練習問題

それでは、斜方投射の問題を解いてみましょう。以下の問題の答えは何でしょうか。

地面との角度がθとなるようにボールを初速度\(v’\)で斜め上に投射しました。

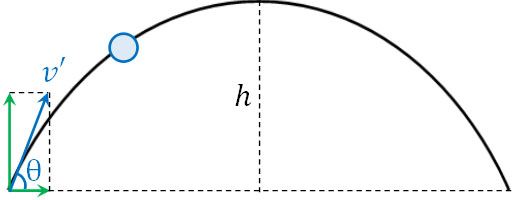
最高点に達するまでの時間\(t\)と高さ\(h\)を求めましょう。
ボールが地面に到着するとき、水平方向に移動した距離を計算しましょう。

1) 最高点に達するまでの時間\(t\)と高さ\(h\)を求めましょう

斜方投射では、水平方向と鉛直方向にベクトルを分解して計算しましょう。最高点への到達で考慮しなければいけないのは鉛直方向のベクトルです。地面との角度がθなので、鉛直方向の初速度は\(v’sinθ\)です。また、最高点での鉛直方向の速度は0です。

そこで等加速度直線運動の公式に当てはめて計算しましょう。

\(v=v_0+at\)

\(0=v’sinθ-gt\)

\(t=\displaystyle\frac{v’sinθ}{g}\)

こうして、最高点への到達時間は\(\displaystyle\frac{v’sinθ}{g}\)とわかります。同様に公式を利用し、高さを求めましょう。

\(v^2-v_0^2=2ax\)

\(0-v’^2sin^2θ=-2gh\)

\(h=\displaystyle\frac{v’^2sin^2θ}{2g}\)

最高点の高さは\(\displaystyle\frac{v’^2sin^2θ}{2g}\)と計算できました。

2) ボールが地面に到着するとき、水平方向に移動した距離を計算しましょう

ボールが最高点に達するまでの時間を2倍すると、ボールが地面に到着する時間になります。ボールを投射する位置とボールが到着する地面の位置は高さが等しいからです。最高点への到達時間は\(\displaystyle\frac{v’sinθ}{g}\)なので、地面に到着する時間は\(\displaystyle\frac{2v’sinθ}{g}\)です。

また水平方向の速さは\(v’cosθ\)です。水平方向は等速直線運動となるため、速さと経過時間をかけることによって水平方向の移動距離を計算できます。つまり、答えは以下のようになります。

\(v’cosθ×\displaystyle\frac{2v’sinθ}{g}\)

\(=\displaystyle\frac{2v’^2sinθcosθ}{g}\)

こうして、水平方向への移動距離は\(\displaystyle\frac{2v’^2sinθcosθ}{g}\)と計算できました。

モンキーハンティング：空中での2物体の衝突

ここまで解説した内容の応用問題としてモンキーハンティングがあります。ハンターがサルに銃弾を当てるとき、発砲と同時に大きな音が出るため、サルは驚いて木から落ちてしまいます。この状況にて、どのようにサルに銃弾を当てて仕留めるのか考えるのがモンキーハンティングです。

斜方投射と自由落下を組み合わせる物理の問題がモンキーハンティングであり、空中での2物体が衝突するにはどうすればいいのかを考えるのです。

それでは、実際に問題を解いてみましょう。

原点からボールAを地面との角度がθとなるように速さ\(v’\)で打ち出します。同時に原点から水平方向に\(l\)離れ、高さ\(h\)の位置からボールBを自由落下させます。なお重力加速度は\(g\)であり、空気抵抗は無視できます。また、「ボールAを発射する位置」「ボールBを落とす位置」「ボールBが地面に到着する位置」を結ぶと直角三角形になります。

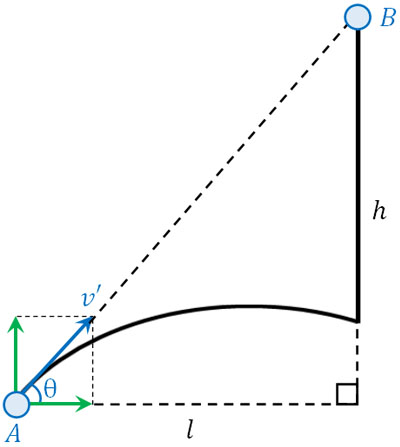
経過時間が\(t\)のとき、ボールAとボールBの高さを求めましょう。
ボールAとボールBが衝突するとき、ボールBを落とすときの高さ\(h\)を求めましょう。
ボールBが地面に到達する前にボールAがボールBに当たるとき、ボールAの初速度\(v’\)の条件を\(g,l,h\)を利用して示しましょう。

1) 経過時間が\(t\)のとき、ボールAとボールBの高さを求めましょう

まず、ボールAの座標を計算しましょう。これまで説明したやり方によって斜方投射のたて軸を計算します。なお鉛直方向の初速度は\(v’sinθ\)です。

\(x=v_0t+\displaystyle\frac{1}{2}at^2\)

\(x=v’sinθ·t-\displaystyle\frac{1}{2}gt^2\)

こうして、ボールAの高さは\(v’sinθ·t-\displaystyle\frac{1}{2}gt^2\)とわかりました。次に、ボールBは自由落下するため、移動距離は以下のようになります。

\(x=v_0t+\displaystyle\frac{1}{2}at^2\)

\(x=0-\displaystyle\frac{1}{2}gt^2\)

\(x=-\displaystyle\frac{1}{2}gt^2\)

なお、高さ\(h\)から自由落下させているため、\(t\)秒後のボールBの高さは\(h-\displaystyle\frac{1}{2}gt^2\)です。

2) ボールAとボールBが衝突するとき、ボールBを落とすときの高さ\(h\)を求めましょう。

ボールAとボールBが衝突するためには、衝突時の高さが同じである必要があります。そこで、先ほど計算したボールAの高さとボールBの高さをイコールで結びましょう。

\(v’sinθ·t-\displaystyle\frac{1}{2}gt^2=h-\displaystyle\frac{1}{2}gt^2\)

\(v’sinθ·t=h\)

こうして、ボールBを落とす高さ\(h\)は\(v’sinθ·t\)とわかりました。

3) ボールBが地面に到達する前にボールAがボールBに当たるとき、ボールAの初速度\(v’\)の条件を\(g,l,h\)を利用して示しましょう

照準が正確であっても、ボールAの速度が遅いとボールBは先に地面に落下してしまいます。そこで、ボールAはある程度の速さがなければいけません。

ボールAがボールBに当たるためには、ボールの時間を考えましょう。ボールBが地面に到着するよりも前に、ボールAが水平方向に距離\(l\)を動けば、ボールAとボールBは衝突します。そこで、ボールBが地面に到着する時間とボールAが距離\(l\)を移動する時間を計算しましょう。

ボールBが地面に到着する時間\(t_B\)は以下になります。

\(x=v_0t+\displaystyle\frac{1}{2}at^2\)

\(h=0-\displaystyle\frac{1}{2}gt_B^2\)

\(t_B^2=\displaystyle\frac{2h}{g}\)

\(t_B=\sqrt{\displaystyle\frac{2h}{g}}\) \((t_B>0)\)

次に、ボールAが距離\(l\)を移動する時間\(t_A\)を計算しましょう。ボールAの水平方向の速度は\(v’cosθ\)なので、以下のようになります。

\(l=v’cosθ×t_A\)

\(t_A=\displaystyle\frac{l}{v’cosθ}\)

こうして、\(t_A\)と\(t_B\)を得ることができました。ボールAとボールBが衝突するためには、ボールBが地面に到着する時間\(t_B\)よりも、ボールAが距離\(l\)を移動する時間\(t_A\)が小さければいいです。言い換えると、\(t_A<t_B\)であればボールAはボールBに衝突します。

そこで、以下のように計算しましょう。

\(t_A<t_B\)

\(\displaystyle\frac{l}{v’cosθ}<\sqrt{\displaystyle\frac{2h}{g}}\)

\(v’>\sqrt{\displaystyle\frac{g}{2h}}·\displaystyle\frac{l}{cosθ}\)

なお問題文より、「ボールAを発射する位置」「ボールBを落とす位置」「ボールBが地面に到着する位置」を結ぶと直角三角形になるため、\(cosθ=\displaystyle\frac{l}{\sqrt{h^2+l^2}}\)です。そこで、先ほどの式に代入しましょう。

\(v’>\sqrt{\displaystyle\frac{g}{2h}}·l·\displaystyle\frac{\sqrt{h^2+l^2}}{l}\)

\(v’>\sqrt{\displaystyle\frac{g(h^2+l^2)}{2h}}\)

こうして、初速度\(v’\)の条件は\(v’>\sqrt{\displaystyle\frac{g(h^2+l^2)}{2h}}\)になると計算できました。