原子を学ぶとき、電子の状態を知ることが重要になります。電子は荷電しており、最も小さい電気量を電気素量といいます。
電子の電気素量は1900年代に明らかになっています。それでは、かつての科学者はどのようにして電子という非常に小さい物質がもつ電気量を測定したのでしょうか。
これを理解するためには、2つの実験を学ぶ必要があります。一つはトムソンの実験であり、この実験によって電子の比電荷を得ることができます。また、もう一つの実験がミリカンの油滴実験であり、この実験によって電気素量が判明しました。
そこでそれぞれの実験内容を学び、どのように電子がもつ電気量を計算したのか理解しましょう。
もくじ
トムソンの実験:クルックス管(放電管)と陰極線(電子線)
ガラス管に電極を入れ、ガラス管内の空気を抜き、数千ボルトの高い電圧をかけると、電極間でひも状の光が発せられます。このとき利用されるガラス管をクルックス管(放電管)といいます。
クルックス管(放電管)の中に含まれている気体により、電極間で生じる光の色が変化します。ただ陽極側のガラス管壁で発生する光については、クルックス管の中に存在する気体の種類に関係なく、黄緑色の蛍光となります。

それでは、なぜクルックス管の中に存在する気体に関係なく、陽極側のガラス管壁では同じ色の蛍光を発するのでしょうか。当時の科学者は次のように考えました。
- 陰極から何らかの物質が発せられており、陽極側の壁にぶつかることで蛍光を発している。そのため、放電管内の気体の種類に関係なく黄緑色の蛍光を生じる。
科学者は正体不明の物質によって作られる線を陰極線と名付けました。なお、後になって陰極線の正体は電子とわかります。そのため、陰極線は電子線とも呼ばれています。
「陰極線の正体は電子である」と1897年に発見したのがイギリスの科学者であるトムソンです。これをトムソンの実験といいます。
力のつり合いを利用し、比電荷の式を得る
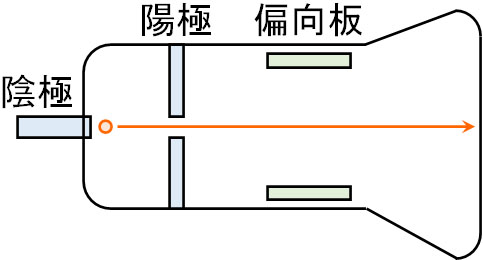
それでは、どのようにしてトムソンは「陰極線が負の電荷をもつ粒子の流れである」と解明したのでしょうか。トムソンの実験では、陰極と陽極、偏向板を用意します。偏向板に電圧をかけない場合、以下のように粒子(電子)はまっすぐ進みます。
次に、偏向板に電圧を加えます。そうすると、陰極線はプラスの電荷をもつ側へ曲がります。そのため、陰極線はマイナスの電荷をもつ粒子であるとわかりました。
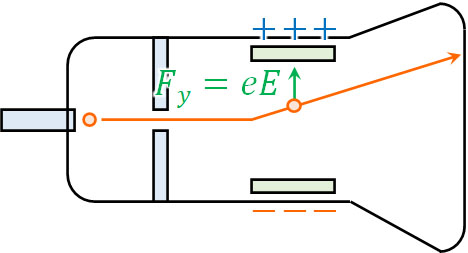
このとき、長さ\(l\)の偏光板に電圧をかけると、電場\(E\)が発生します。電子の電気量を\(-e\)とすると、\(y\)軸方向に加わる力\(F_y\)は\(F_y=eE\)となります。
なお電子の質量を\(m\)、\(y\)軸方向の加速度を\(a_y\)とすると、\(F_y=ma_y\)の式を作ることができます。つまり、以下の式が成り立ちます。
\(ma_y=eE\)
\(a_y=\displaystyle\frac{eE}{m}\)
こうして、粒子(電子)が偏向版を通過するときに加わる加速度\(a_y\)を得ることができました。
また陽極から発射された電子が等しい速さ\(v\)で動いている場合、偏向板の長さ\(l\)を利用し、偏向板を通過する時間\(t\)を以下のように表すことができます。
\(vt=l\)
\(t=\displaystyle\frac{l}{v}\)
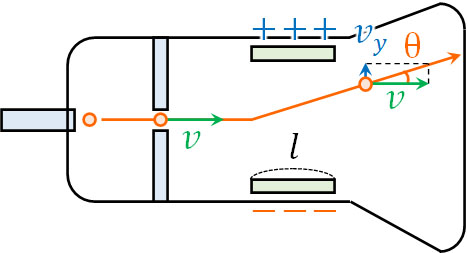
加速度が\(a_y=\displaystyle\frac{eE}{m}\)、経過時間が\(t=\displaystyle\frac{l}{v}\)であるため、等加速度直線運動の公式より、以下のように\(y\)軸方向の速さ\(v_y\)を計算できます。
\(v_y=a_yt\)
\(v_y=\displaystyle\frac{eE}{m}×\displaystyle\frac{l}{v}\)
\(v_y=\displaystyle\frac{eEl}{mv}\)
また図より、以下のように\(tanθ\)を表すことができます。
\(tanθ=\displaystyle\frac{v_y}{v}\)
\(tanθ=\displaystyle\frac{eEl}{mv^2}\)
この式を変形して、\(\displaystyle\frac{e}{m}\)の形にしましょう。
- \(\displaystyle\frac{e}{m}=\displaystyle\frac{v^2}{El}tanθ\)
こうして、粒子(電子)の電気量を重さで割るときの関係を計算することができました。\(\displaystyle\frac{e}{m}\)は電子がもつ電気量と質量の比であるため比電荷といいます。
ローレンツ力を利用し、電子の比電荷を計算する
次に、先ほどのクルックス管(放電管)に対して磁場を加えましょう。電子は磁場の影響を受けて曲がります。つまり、磁場によって電子は力を受けるのです。そこで陰極線(電子線)がまっすぐ進むように磁場(磁束密度\(B\))を加えます。
このとき以下のように、磁束密度\(B\)が画面の表側から裏に向かって進んでいるとします。
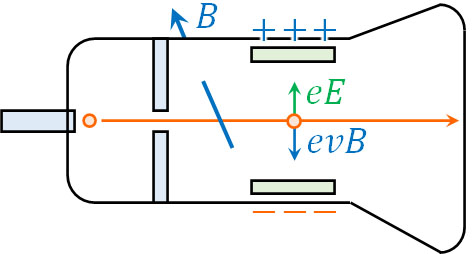
フレミングの左手の法則を利用すると、粒子(電子)は偏光板の負極側に力が加わるとわかります。ローレンツ力の公式より、ローレンツ力\(f\)は\(f=evB\)です。つまり、電場による力と磁場(磁束密度)によるローレンツ力がつり合います。そこで、以下の計算をしましょう。
\(eE=evB\)
\(v=\displaystyle\frac{E}{B}\)
そこで\(\displaystyle\frac{e}{m}=\displaystyle\frac{v^2}{El}tanθ\)と\(v=\displaystyle\frac{E}{B}\)を利用して、以下のように計算しましょう。
\(\displaystyle\frac{e}{m}=\displaystyle\frac{v^2}{El}tanθ\)
\(\displaystyle\frac{e}{m}=\displaystyle\frac{E}{B^2l}tanθ\)
磁場\(E\)、磁束密度\(B\)、偏向板の長さ\(l\)、\(tanθ\)はすべて測定可能です。そのため、電子の比電荷を計算することができます。
トムソンは何度も実験を行い、陰極線粒子の比電荷が常に同じ値になることを発見しました。つまり、陰極線は一つの粒子によって発生すると明らかにしたのです。
電子の電気素量を得た最初の実験がミリカンの油滴実験
ただトムソンの実験でわかったのは比電荷であり、一つの電子がもつ電気量(電気素量)はわかっていません。また、電子の質量\(m\)もわかっていません。
そうしたとき、電子の電気量\(e\)と電子の質量\(m\)を初めて測定したのがアメリカの物理学者であるミリカンです。彼は1909年、電気素量の計測に成功しました。この実験がミリカンの油滴実験です。どのようにして、彼は電気素量を計測したのでしょうか。
霧吹きを利用することにより、小さな油滴を作ることができます。このとき極板に開けた小さい穴から油滴を落下させます。また、油滴にX線を当てることで帯電させることができます。

このような装置を利用してミリカンは実験を行いました。なお極板は金属板であるため、電圧をかけることによって電場を発生させることができます。
電圧をかけない場合とかける場合の力のつり合い
まず、極板に電圧をかけない場合の力のつり合いを考えましょう。油滴の質量を\(m\)、重力加速度を\(g\)とするとき、油滴に加わる重力は\(mg\)です。
ただ油滴は軽く、空気抵抗によってすぐに終端速度(空気抵抗により、加速していない一定スピード)に達します。油滴は加速度のない落下をするため、空気抵抗による比例定数を\(k\)、終端速度を\(v_1\)とすると、力のつり合いは以下のようになります。
\(mg=kv_1\)
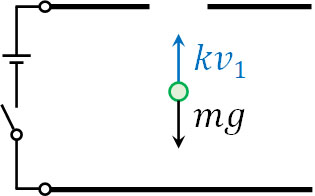
また\(mg=kv_1\)を変形すると、\(m=\displaystyle\frac{kv_1}{g}\)となります。
次に、極板に電圧をかけましょう。この場合、極板に電位差を生じることで電場\(E\)が発生します。油滴の電気量を\(-q\)とすると、静電気力(クーロン力)によって油滴は正電荷に引き寄せられます。また、電圧をかけて油滴を上昇させるときに発生する静電気力は\(F=qE\)です。
なお油滴が上昇するとき、空気抵抗が先ほどとは逆向きに加わります。そのため上昇の速さが\(v_2\)の場合、以下のつり合いの式を作ることができます。
\(qE=mg+kv_2\)
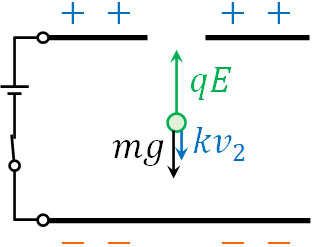
油滴の重さ\(m\)を調べるのは困難です。そこで\(m=\displaystyle\frac{kv_1}{g}\)を\(qE=mg+kv_2\)に代入しましょう。
\(qE=mg+kv_2\)
\(qE=\displaystyle\frac{kv_1}{g}×g+kv_2\)
\(qE=k(v_1+v_2)\)
\(q=\displaystyle\frac{k(v_1+v_2)}{E}\)
こうして、油滴の電気量は\(q=\displaystyle\frac{k(v_1+v_2)}{E}\)になるとわかります。また比例定数\(k\)は値が決まっており、速さ\(v_1\)、速さ\(v_2\)、電場\(E\)は測定できるため、油滴がもつ電気量を計算できます。
油滴実験を用いて電子の電気素量と質量を得る
ミリカンはこの油滴実験を行い、多くの油滴の電気量\(q\)を計算しました。当然、それぞれ油滴によって大きさが異なるため、実験によって油滴がもつ電気量\(q\)の値は異なります。油滴には多くの電子が存在するからです。
ただ、彼は多くの油滴の電気量\(q\)を測定することにより、すべてのケースにおいて、電気量が\(e≒1.6×10_{-19}\)[C]の整数倍になることを発見しました。この値が電気素量\(e\)です。電気素量は電気量の最小単位であるため、必ず整数倍になるのです。
また先ほど、トムソンの実験を解説しました。トムソンの実験では、比電荷\(\displaystyle\frac{e}{m}\)は以下の値になるとわかっています。
- \(\displaystyle\frac{e}{m}≒1.759×10^{11}\)
電気素量\(e\)がわかったため、\(\displaystyle\frac{e}{m}\)に値を代入すると電子の質量を計算できます。
- \(m≒9.1×10^{-31}\)
こうして、電子の質量は\(m≒9.1×10^{-31}\)[kg]であるとわかりました。
電子の比電荷と電気素量を得る方法を学ぶ
電子がもつ電気量や質量を実験によって測定するとなると、不可能に思えてしまいます。ただ、電子の比電荷や電気素量、質量はかなり昔に実験によって明らかにされています。そこで原子を学ぶとき、かつての科学者がどのように実験をしたのか学びましょう。
陰極線の正体を明らかにしたのがトムソンであり、彼によって行われた実験をトムソンの実験といいます。トムソンの実験により、電子の比電荷がわかりました。
またミリカンによって油滴を用いた実験が行われ、これによって電子がもつ電気量(電気素量)がわかりました。また比電荷と電気素量を利用することにより、電子の質量がわかります。測定可能な値を利用することにより、測定が困難な値を彼らは明らかにしたのです。
原子を学ぶとき、トムソンの実験とミリカンの油滴実験は基本的な内容なので、必ず実験内容を理解しましょう。