高校物理で学ぶ内容がばねの弾性力です。ばねを伸ばす、または縮めることによって力が発生します。このとき発生する力が弾性力です。
ばねの弾性力を計算するとき、フックの法則を利用します。フックの法則を覚える必要はないものの、定数とばねの伸びの長さをかけることによって弾性力を得られることを理解しましょう。これにより、力のつり合いを用いて式を作ることができます。
また複数のばねを利用するケースは多いです。ばねのつなぎ方には並列と直列があり、合成ばね定数がどのように変化するのか学びましょう。
力のつり合いを考えるとき、ばねによる力(弾性力)を理解することは重要です。そこで、どのように弾性力や力のつり合いの計算をすればいいのか解説していきます。
もくじ
ばね定数とフックの法則
ばねを伸ばす、または縮めると力が働くことは容易に想像できます。ばねが自然長に戻ろうとする力を弾性力といいます。ばねを伸ばすほど、または縮めるほどばねの弾性力は強くなります。
それでは、ばねの弾性力はどのように計算すればいいのでしょうか。ばねの弾性力は、ばねを伸ばす長さ(またはばねを縮める長さ)に比例します。イギリスの物理学者ロバート・フックが提唱したため、この法則をフックの法則といいます。
ばねは固有のばね定数(比例定数)\(k\) N/mをもっています。フックの法則を利用すれば、比例定数\(k\)と自然長との長さのズレ\(x\) mを利用して、以下のようにばねの弾性力\(F\) Nを計算できます。
- \(F=kx\)
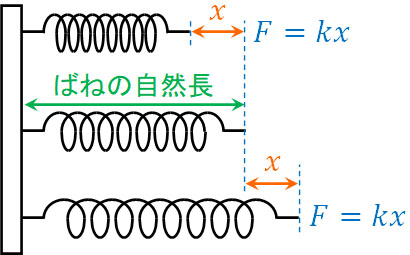
強いばねであれば比例定数\(k\)が大きく、少し伸ばすだけでも弾性力が大きいです。一方で力の弱いばねであれば比例定数\(k\)は小さいです。
いずれにしても、弾性力を計算するときは比例定数\(k\)と自然長との長さのズレ\(x\)をかけましょう。
力の大きさは定数と値をかけることで得られる
なおフックの法則を覚える必要があるかというと、覚えなくても問題ありません。それよりも重要なのは、力を表すときは定数と値をかけるという事実です。例えば物体に加わる重力\(F\)は重さ\(m\)と重力加速度\(g\)をかけることによって得られます。
- \(F=mg\)
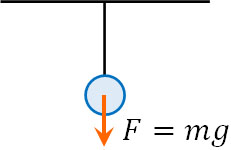
重力加速度\(g\)は一定であり、すべての物体に対して共通の定数です。ただ物体の重さはそれぞれ異なり、重さに比例して物体に加わる重力が大きくなります。
同様に、ばねは比例定数\(k\)をもちます。また、ばねを伸ばすほどばねの弾性力は大きくなります。そこで、比例定数とばねの自然長とのズレ\(x\)をかけるのです。このように考えると、物体に加わる重力もばねの弾性力も計算方法は同じとわかります。
・ばねを伸ばすとき、縮めるときの力の向き
なお、ばねを伸ばすとき(または縮めるとき)の力の向きを理解しましょう。
ばねは自然長に戻ろうとするため、ばねが伸びているとき、ばねは物体を引っ張ります。それに対して、ばねが縮んでいるとき、ばねは物体を押します。以下のようになります。
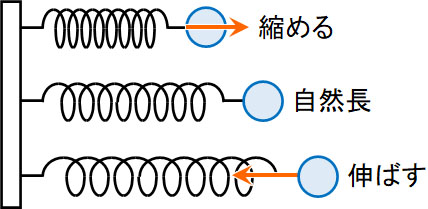
図に記しているように、ばねが実際に伸びているときや縮んでいる場面を想像すれば、ばねによる力の向きがわかります。
ばねの弾性力と重りとの力のつり合い
それでは、ばねの弾性力に関して練習問題を解いてみましょう。
- 重さを無視できるばねを利用し、下図のように球をつるしました。ばね定数を\(k\)、球の重さを\(m\)、重力加速度を\(g\)とするとき、ばねの伸びを求めましょう。
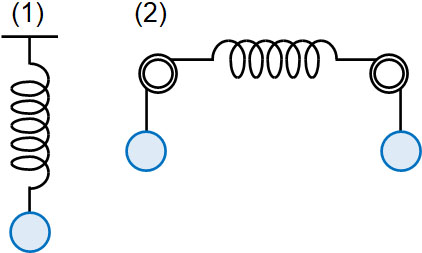
1)
まず、力のつり合いを考えましょう。球の重さは\(m\)であるため、\(mg\)の力でばねを引っ張っています。同時に、ばねは同じ力\(kx\)で球を引っ張ることで静止しています。
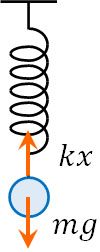
そのため、以下の式を作ることができます。
\(mg=kx\)
\(x=\displaystyle\frac{mg}{k}\)
こうして、ばねの長さは\(x=\displaystyle\frac{mg}{k}\) mとなります。
2)
球とばねに働く力を図示しましょう。以下のようになります。
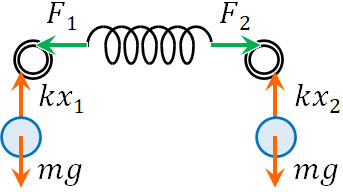
ばねに着目するとき、\(F_1\)と\(F_2\)の2つの力が働いているとわかります。また静止しているため、\(F_1=F_2\)です。
次に球に着目すると、\(mg=kx_1\)とわかります。また\(F_1\)というのは、球の重さに依存しています。言い換えると、作用・反作用の法則が働いています。つまり\(F_1=mg=kx_1\)です。
同様に考えると、\(F_2=mg=kx_2\)です。そのため、以下の関係が成り立ちます。
\(F_1=F_2=kx_1=kx_2=mg\)
つまり\(x_1=\displaystyle\frac{mg}{k}\)であり、\(x_2=\displaystyle\frac{mg}{k}\)です。ばねが伸びる長さは問1と同じです。
球が2つあるため、ばねは2倍伸びるように思った人がいるかもしれません。ただ片側を壁と捉えると、なぜ先ほどの問題と比べて答えが同じになるのか理由がわかります。
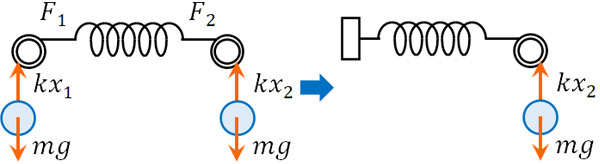
物体は静止しているため、片側を壁に変えても問題なく、このように考えることによって物理現象をとらえやすくなります。
並列での合成ばね定数
ここまで、一つのばねが存在する場面を解説してきました。それでは、複数のばねが存在する場合はどのように考えればいいのでしょうか。まず、以下のように並列でばねをつなぐ場面を考えましょう。
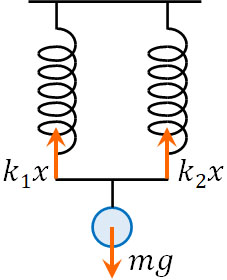
複数のばねを並列につなぐ場合、1つのばねが存在するときに比べて、重りを引っ張る力が強くなるのは容易に想像できます。1つのばねよりも、100個のばねがあるほうが重りを引っ張る力は強いです。当然、1つよりも2つのばねのほうが引っ張る力(比例定数)は大きくなります。
それでは、具体的な合成ばね定数を計算しましょう。ばねは静止しているため、球による重力と2つのばねによって押し上げられる力がつりあっています。
またばねが伸びるとき、2つのばねが伸びる長さ\(x\)は同じです。違うのは2つのばねの比例定数です。そのため、以下の式を作ることができます。
\(k_1x+k_2x=mg\)
\((k_1+k_2)x=mg\)
ここで、並列に存在する2つのばねについて、仮に1つのばねとみなしましょう。この場合、2つのばねを合体させた合成ばねでは、合成ばね定数\(K\)は\(k_1+k_2\)になるとわかります。
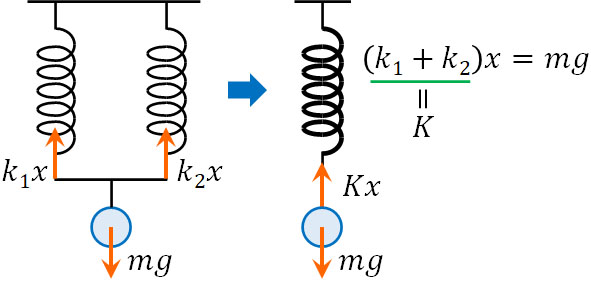
こうして、合成ばね定数を計算します。そのためばねを並列で並べる場合、合成ばね定数\(K\)は以下のようになります。
- \(K=k_1+k_2+k_3+…\)
ばねを並列につなげる場合、ばね定数は大きくなります。言い換えると、ばねを伸ばすときにより大きな力が必要になります。
直列での合成ばね定数
次に、直列でばねをつなげる場合の合成ばね定数を確認しましょう。並列にばねを並べる場合に比べると、2つのばねを直列でつなぐ場合は複雑です。そこで、以下のように3パターンに分けて考えましょう(ばねの重力は無視する)。
- 球に働く力に着目
- ばね1に働く力に着目
- ばね2に働く力に着目
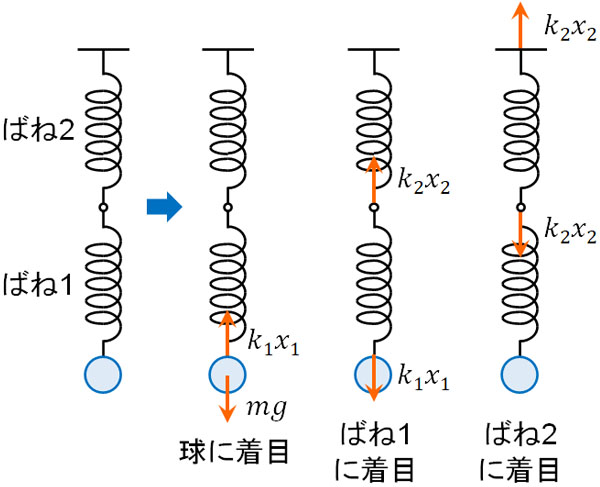
それぞれの物体に働く力に着目すると、上図より、以下の関係がわかります。
- 球に働く力に着目:\(mg=k_1x_1\)
- ばね1に働く力に着目\(k_1x_1=k_2x_2\)
つまり、以下の関係が成り立ちます。
- \(mg=k_1x_1=k_2x_2\)
この式からわかることは何でしょうか。球の重さ\(mg\)は、ばね1とばね2の両方に加わります。また、ばね1では\(x_1\) m伸び、ばね2では\(x_2\) m伸びます。そのため、ばね1つのときに比べて、直列につなぐとばねがより伸びます。
直列にばね1とばね2をつないでいる場面と、ばね1のみを使用している場面を考えてみましょう。この場合、以下の関係が成り立ちます。
- ばね2つの場合:\(mg=k_1x_1=k_2x_2\)
- ばね1つの場合:\(mg=k_1x_1\)
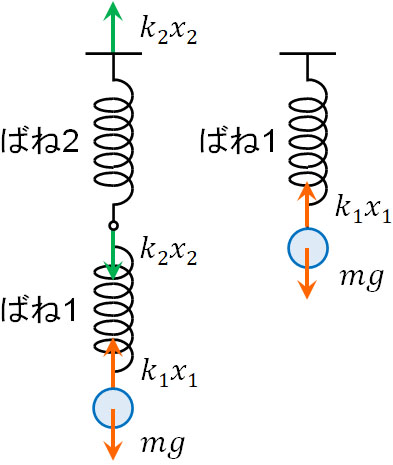
ばね1つだと働く力は\(mg=k_1x_1\)だけです。一方、ばねが2つあると\(mg=k_1x_1\)に加えて、\(mg=k_2x_2\)の影響が加わります。球の重さ\(mg\)によってばね1が\(x_1\)m伸ばされ、同じ重さ\(mg\)によってばね2が\(x_2\)m伸ばされるのです。これが、直列でばねをつなぐとばねが伸びやすくなる理由です。
ばねが伸びやすくなるというのは、合成ばね定数の比例定数\(K\)が小さくなることを意味します。
なお\(mg=k_1x_1\)より、ばね1での伸びは\(x_1=\displaystyle\frac{mg}{k_1}\)です。また\(mg=k_2x_2\)より、ばね2での伸びは\(x_2=\displaystyle\frac{mg}{k_2}\)です。
・直列でつなぐ場合のばね定数
それでは直列でばねをつなぐ場合、どのように比例定数を求めればいいのでしょうか。先ほどと同じように、2つのばねを直列でつないだケースについて、仮に1つのばねと仮定しましょう。この場合、ばねの伸びは\(x_1\)と\(x_2\)の合計なので、以下の関係式が成り立ちます。
- \(K(x_1+x_2)=mg\)
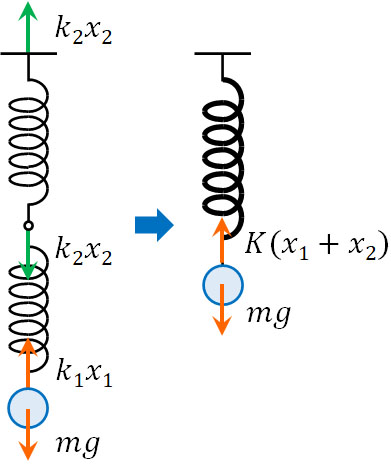
そこでへ\(x_1=\displaystyle\frac{mg}{k_1}\)と\(x_2=\displaystyle\frac{mg}{k_2}\)を代入しましょう。
\(K(x_1+x_2)=mg\)
\(K\left(\displaystyle\frac{mg}{k_1}+\displaystyle\frac{mg}{k_2}\right)=mg\)
\(K\left(\displaystyle\frac{1}{k_1}+\displaystyle\frac{1}{k_2}\right)=1\)
\(\displaystyle\frac{1}{K}=\displaystyle\frac{1}{k_1}+\displaystyle\frac{1}{k_2}\)
つまり直列でばねをつなげる場合、合成ばね定数\(K\)は以下のようになります。
- \(\displaystyle\frac{1}{K}=\displaystyle\frac{1}{k_1}+\displaystyle\frac{1}{k_2}+\displaystyle\frac{1}{k_3}+…\)
この公式を得るのは難しいため、直列での合成ばね定数を得る公式は覚えてもいいです。重要なのは、「直列でばねをつなぐことによって合成ばね定数が小さくなり、ばねが伸びやすくなる」という事実です。
ばねの弾性力に関する練習問題
並列にばねをつなぐ場合、比例定数を足せばいいので容易に計算できます。そこで、直列でばねをつないだ場合の練習問題を解きましょう。以下の問題の答えは何でしょうか。
- ばね定数がそれぞれ10N/mと20N/mの2本のばねを直列につなぎ、質量1kgの重りをつるしました。なお、重力加速度は\(g\)です。
- それぞれのばねの伸び\(x_1\)と\(x_2\)はいくらですか。
- 2本のばねを一本のばねとみなす場合、合成ばね定数はいくらですか。
1) それぞれのばねの伸び\(x_1\)と\(x_2\)はいくらですか
直列にばねをつなぐ場合、2本のばねに対して、それぞれ同じ重力が加わります。そのため、以下のように計算しましょう。
\(10x_1=20x_2=1\)
これを解くと\(x_1=0.1\)mであり、\(x_2=0.05\)mとわかります。
2) 2本のばねを一本のばねとみなす場合、合成ばね定数はいくらですか
先ほど解説した公式を利用して合成ばね定数を計算しましょう。以下のようになります。
\(\displaystyle\frac{1}{K}=\displaystyle\frac{1}{10}+\displaystyle\frac{1}{20}\)
\(\displaystyle\frac{1}{K}=\displaystyle\frac{3}{20}\)
\(K=\displaystyle\frac{20}{3}\)
こうして、合成ばね定数は\(\displaystyle\frac{20}{3}\) N/mとわかりました。
なお\(K=\displaystyle\frac{20}{3}≒6.67\)であり、10N/mや20N/mに比べて比例定数が小さいとわかります。そのため計算によっても、直列でばねをつなぐとばね定数が小さくなることがわかります。
ばねを含む力学の問題ではフックの法則を利用する
力のつり合いを学ぶとき、ばねに関する力学を理解しなければいけません。物理でばねを学ぶときはフックの法則が重要であり、比例定数とばねを伸ばす長さ(またはばねを縮める長さ)をかけることによってばねの弾性力を計算できます。
このとき物体が静止しているのであれば、力のつり合いが取れています。そこで重りやばねに着目し、力の大きさやベクトルを正確に図示できるようになりましょう。
また、複数のばねを利用する場面は多いです。ばねを並列でつないだり、直列でつないだりするのです。ばねを並列でつなぐ場合、ばね定数を足すことによって合成ばね定数を得られます。一方でばねを直列でつなぐ場合、ばね定数は低くなります。
機械工学でばねは必須であり、多くの機器でばねが利用されています。こうした機器類の設計をするとき、ここまで解説した計算が必要になります。そこで、ばねの弾性力の計算方法を理解しましょう。






