原子について学ぶとき、重要な内容の一つが光電効果です。私たちは物理で「光は波である」と学びます。光に波としての性質があるのは実験によって証明されています。
ただ、光には粒子としての性質もあります。これを光量子仮説といいます。光が粒子としての性質をもつ理由として、光電効果が知られています。アインシュタインが光量子仮説を提唱し、光電効果が起こる原理を説明しました。
それでは、光電効果とは何なのでしょうか。また、光電効果で利用される公式は何を意味しているのでしょうか。
公式を暗記しても意味がなく、公式がもつ意味や原理を学び、式を利用してグラフを描けるようになる必要があります。そこで、光電効果が起こる原理や光量子仮説の詳細を解説していきます。
もくじ
金属に光を当てると電子が飛び出す
金属に光を当てることにより、金属表面から電子が飛び出してくる現象が知られています。この現象を光電効果といいます。
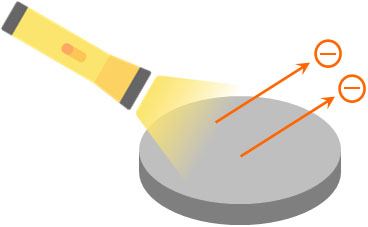
電子が金属表面から飛び出すためには、その分だけエネルギーが必要になります。つまり、光が電子にエネルギーを与えることにより、光エネルギーが運動エネルギーに変換されるのです。このとき、金属表面から飛び出す電子を光電子といいます。
光電効果でわかっている事実:限界振動数
それでは、なぜ光電効果が重要なのでしょうか。実験によって、光電効果には以下の性質があると明らかになっています。
・光の振動数によって光電効果が起こるかどうかが決まる
すべての光で光電効果が起こるわけではありません。光電効果が起こるためには振動数\(f\)が重要であり、光の振動数が特定の値(限界振動数)よりも小さい場合、どれだけ長時間、強い光を当てても金属から光が飛び出ることはありません。
一方、限界振動数よりも大きな値であれば、光を当てることによって、弱い光であっても金属から電子が飛び出ます。
・飛び出す電子の運動エネルギーは光の振動数で決まる
電子が飛び出すとき、当然ながら速さがあります。このときのスピード(運動エネルギー)は当てる光の振動数に依存します。つまり光の強さ(光の振幅)は関係なく、飛び出す電子の速さを決めるのは光の振動数となります。
・光を強くすると、飛び出す電子の量が増える
光の強さ(光の明るさ)に関与しているのが振幅です。波の幅が大きいほど振幅が大きくなり、それに伴って光は明るくなります。
前述の通り、光の強さは運動エネルギー(電子の速さ)に関与しません。一方、明るい光であるほど飛び出す電子(光電子)の量が増えるのです。
光が波の場合、光電効果を説明できない
それでは、なぜ先ほどの事実が重要なのでしょうか。先ほどの実験結果について、以前の物理学の知識では説明することができませんでした。光は波であると考えられており、実験によっても証明されています。ただ光が波である場合、光電効果が起こる理由を説明できないというわけです。
波長が長い光(振動数が小さい光)として、赤色の光が知られています。赤色の光では、どれだけ明るくしても光電効果が起こりません。
それに対して、波長が短い光(振動数が大きい光)として、紫色の光が知られています。光が紫色の場合、暗い光であっても光電効果が起こります。
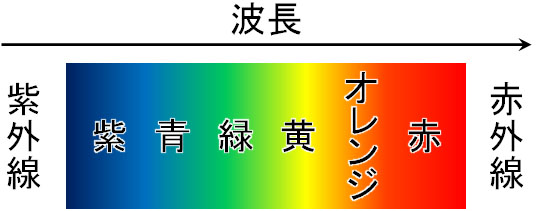
ただ、光エネルギーは波長だけでなく、振幅(光の明るさ)も関与しています。光の色が赤色であっても、紫色であっても、大きなエネルギーをもつ光であれば光電効果が起こらなければいけません。しかし、実際には赤色の光だと金属から電子が飛び出すことはありません。
光が波としての性質のみをもつと考える場合、光電効果の説明ができません。そのため、当時は多くの物理学者が光電効果の説明をすることができず、悩みました。
光の粒子性:アインシュタインによる光量子仮説
光電効果が起こる理由を説明したのがアインシュタインです。彼は光を以下のように説明しました。
- 光は粒子としての性質がある
光は波としての性質があり、前述の通りこの事実は既に実験として証明されています。そのため「光というのは、波に加えて、粒子としてもふるまう」とアインシュタインは考えたのです。これを光量子仮説といいます。
ただ、この考え方は意味不明です。粒子というのは、衝突することによってはね返ります。一方で波の場合、独立性があり、衝突することはなくすり抜けます。つまり、粒子と波は性質が大きく異なるのです。
それにも関わらず、彼は「光は粒子としての性質があり、波の性質も持つ」と主張したのです。しかし、実験によって理論を証明できる場合、物理ではそれで問題ありません。
物理では、理由が解明されていない現象が非常に多いです。ただ、実験でそのように示されている場合、ひとまず受け入れなければいけません。理論として変であっても、実験によって証明されている以上、納得する必要があるのです。
参考までに、アインシュタインがノーベル物理学賞を受賞した理由は相対性理論ではなく、光電効果の解明(光量子仮説の提唱)です。
光子がもつエネルギーの公式:プランク定数
光の粒子を光子(こうし)といいます。光子がエネルギーをもつことにより、金属に当たることによって電子が飛び出るのです。
それでは、一つの光子がもつエネルギーはどのように表されるのでしょうか。光の振動数を\(ν\)(ニュー)とするとき、一つの光子がもつエネルギー\(E\)を以下の公式によって得ることができます。
- \(E=hν\)
\(h\)はプランク定数と呼ばれており、比例定数です。\(h≒6.6×10^{-34}\)[J·s]であり、値は決まっています。また前述の通り\(ν\)は振動数であり、振動数\(f\)と意味は同じです。ひとまず、プランク定数と振動数をかけると光子がもつエネルギーを得ることができます。
また波の公式より、\(v=fλ\)です。そこで振動数\(f\)を振動数\(ν\)に変え、速さ\(v\)を光の速さ\(c\)に変えましょう。そうすると\(c=νλ\)となり、\(ν=\displaystyle\frac{c}{λ}\)を得ることができます。
そこで\(ν=\displaystyle\frac{c}{λ}\)を\(E=hν\)に代入すると以下のようになります。
- \(E=h\displaystyle\frac{c}{λ}\)
光の速さは決まっています。また\(c=νλ\)であるため、振動数\(ν\)が大きくなると、波長\(λ\)は短くなります。そのため、光子がもつエネルギーは波長\(λ\)に反比例するのです。
運動エネルギーと仕事関数、限界振動数の関係
光が粒子としての性質をもつと仮定すれば、先ほど解説した光電効果を解説することができます。
・光の振動数によって光電効果が起こるかどうかが決まる
一つの光子が一つの電子と衝突し、光子がもつエネルギーが電子に移動するとします。このとき、電子が金属から飛び出すためには、最低でも\(W\)のエネルギーを与えなければいけません。電子が金属から飛び出るために必要な最低限のエネルギー\(W\)を仕事関数といいます。
つまり、以下の関係があります。
- \(hν<W\):電子は金属から飛び出ない
- \(hν≧W\):電子は金属から飛び出る
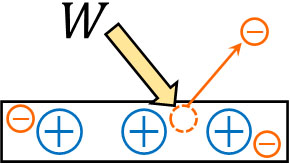
電子は原子核の周辺に存在します。また電子は金属イオンと静電気力によって引き合っているため、小さいエネルギーでは金属から飛び出すことはありません。ただ仕事関数\(W\)よりもエネルギーが大きい場合、電子は外に飛び出るというわけです。
一方で限界振動数よりも小さい場合、光子がもつエネルギーは弱く、仕事関数\(W\)よりもエネルギーが小さいので自由電子を金属表面から引き離すことができません。
なお電子が飛び出す最低の振動数を\(ν_0\)とすると、\(hν_0=W\)となります。そのため、限界振動数は\(ν_0=\displaystyle\frac{W}{h}\)によって計算できます。
・飛び出す電子の運動エネルギーは光の振動数で決まる
一つの光子がもつエネルギーが\(E=hν\)であり、電子を金属から引き離すために必要なエネルギーが仕事関数\(W\)であるため、金属から飛び出た後の電子の最大運動エネルギーは以下のように表すことができます。
- \(\displaystyle\frac{1}{2}mv_{max}^2=hν-W\)
もちろん、\(hν=W+\displaystyle\frac{1}{2}mv_{max}^2\)と考えても問題ありません。なお、なぜ最大の運動エネルギー(最大の速さ\(v_{max}\))を利用しているかというと、電子によって速さが異なるからです。
金属表面に存在する電子の場合、最も少ないエネルギー(仕事関数\(W\))によって金属から飛び出ることができます。一方で金属表面ではなく、金属内部に存在する電子の場合、金属から飛び出るためにはより多くのエネルギーが必要になります。
\(\displaystyle\frac{1}{2}mv_{max}^2=hν-W\)というのは、金属表面に存在する電子に対して適用できる公式です。
・光を強くすると、飛び出す電子の量が増える
光が明るいというのは、光のエネルギーが強いという意味ではなく、光子の数が多いことを意味しています。光子の数が多く、光が明るい場合、当然ながらその分だけ金属から飛び出す電子の量は多くなります。
しかし光子がもつエネルギーが低い場合、\(E=hν\)の値は仕事関数\(W\)よりも低くなり、いくら光が明るくても金属表面から電子が飛び出ることはありません。
光電効果の式とグラフ
このように光を粒子と捉えることにより、光電効果がなぜ起こるのか説明できます。それでは、光電効果の式をグラフにしましょう。先ほど、以下の関係が成り立つと解説しました。
- \(hν=W+\displaystyle\frac{1}{2}mv_{max}^2\)
ここで、\(K_0=\displaystyle\frac{1}{2}mv_{max}^2\)としましょう。つまり、\(K_0\)は電子が飛び出るときの運動エネルギーの最大値です。そこで、以下のように式を変形しましょう。
\(hν=W+\displaystyle\frac{1}{2}mv_{max}^2\)
\(hν=W+K_0\)
\(K_0=hν-W\)
式を確認すると、傾き\(h\)、切片\(-W\)の直線であるとわかります。そこで、以下のようにグラフを描きましょう。
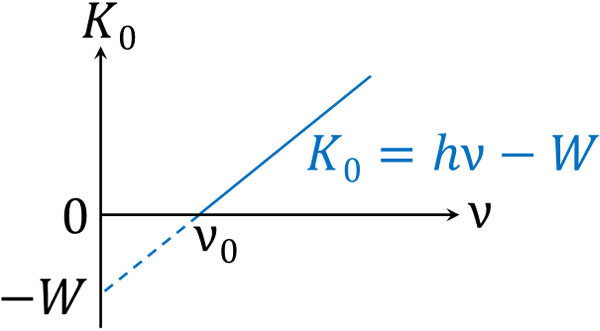
※\(ν_0\)は限界振動数を表します。
電子の運動エネルギー\(K_0\)がゼロのとき、限界振動数\(ν_0\)を得ることができます。また線の傾きはプランク定数\(h\)であり、切片は仕事関数\(W\)です。グラフを利用すると、光電効果で重要な要素を図示することができます。
光電流と阻止電圧:光電効果に関する実験
ここまで説明した内容を理解したうえで、光電効果に関する実験を解説していきます。下図のように金属板Aと金属棒Bに対して導線をつなぎ、光を照射します。
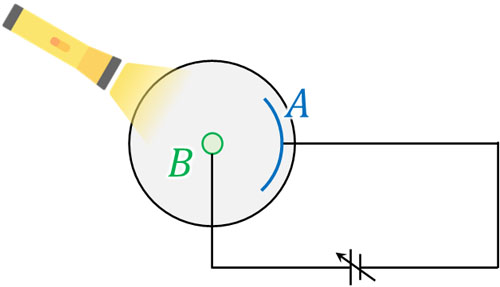
電圧を変えることで、AB間の電位差を変化させ、電子の様子を観察しましょう。このとき、以下の3パターンに分けることができます。
・金属板Aよりも金属棒Bが高電位
金属板Aが負電荷であり、金属棒Bが正電荷の場合、金属板から飛び出た電子は容易に金属棒Bへ到着できます。電子は負の電荷を帯びているため、ほぼすべての電子が正の電荷をもつ金属棒へたどり着けます。
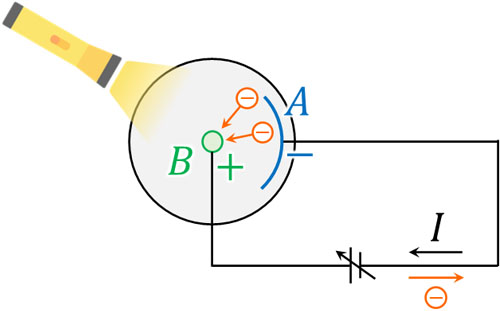
この場合、回路全体では、電子は金属棒Bを伝わることで金属板Aへ動きます。また、電流の向きは電子とは反対になります。つまり、光電効果によって電流\(I\)が流れるのです。この電流を光電流といいます。
・金属棒Bよりも金属板Aが高電位
それでは金属板Aが正に帯電し、金属棒Bが負に帯電する場合はどのような現象が起こるでしょうか。電位差が小さい場合、電子はマイナスの電荷を有しているものの、運動エネルギーがあるので電子の一部が金属棒Bまでたどり着きます。つまり、弱い光電流を生じます。
ただ、さらに電位差を大きくするとすべての電子が金属棒Bにたどりつけなくなります。金属棒は負電荷であるため、同じく負電荷である電子と反発するからです。
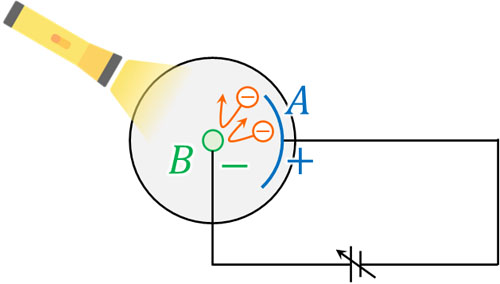
このとき、光電流が流れなくなる電圧を阻止電圧といいます。
光電流と電圧の関係をグラフにする
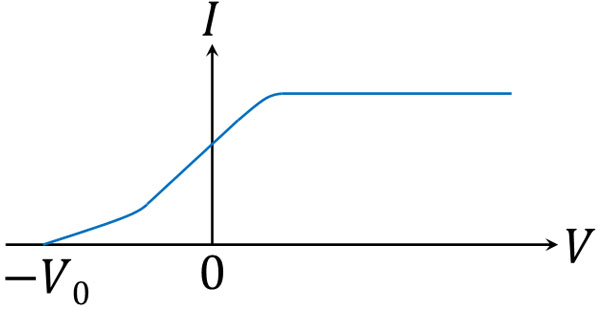
それでは、先ほどの実験結果をグラフにしてみましょう。たて軸を光電流\(I\)、横軸を電圧\(V\)とすると、以下のようなグラフになります。
※光の振動数\(ν\)は一定とします。
金属棒Bが正電荷のときをプラスとすると、電圧が正の値のとき、電圧を高くしても光電流は増えません。これは当然であり、金属棒Bが正に帯電している場合、電子は容易に金属棒Bにたどりつくことができます。そのため、電圧が高くても低くても光電流の大きさに影響しません。
ただ電圧が低くなると、光電流の強さが弱まります。また電圧が負の値になると、さらに光電流の大きさは小さくなります。そうして、阻止電圧\(-V_0\)の部分で光電流がゼロになります。
次に、光の明るさを変えてみましょう。例えば明るさを弱くすると、グラフは以下のように変化します。
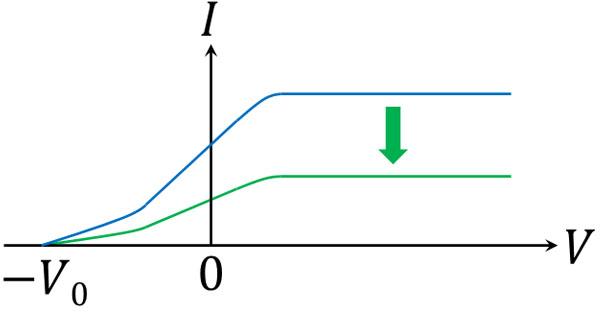
光の明るさが弱くなると、その分だけ光子の数が減り、金属を飛び出す電子の量が減るので光電流は弱くなります。ただ重要なのは、阻止電圧が\(-V_0\)で同じである事実です。
光電効果で説明した通り、一つの光子がもつエネルギーが電子の運動エネルギー(電子の速さ)に関与します。光子がもつエネルギーは振動数に依存するため、光が明るくても暗くても一つの光子がもつエネルギーは変わりません。そのため、光の明るさを変えても電子が飛び出すスピードは変わらず、阻止電圧(金属棒Bにたどり着くかどうか)は変化しないのです。
・阻止電圧と運動量の関係
それでは、阻止電圧と運動量の関係を式にしましょう。阻止電圧では、「金属から飛び出た電子が金属棒Bに到達すると同時に、速度がゼロになった」と考えることができます。そのため、電子の運動エネルギーと静電気力の位置エネルギーを利用して以下の式を作れます。
- \(\displaystyle\frac{1}{2}mv_{max}^2=eV_0\)
※\(m\)は電子の質量、\(e\)は電子の電気量(電気素量)
電子の運動エネルギーがすべて位置エネルギーへと変換されたことを意味するのがこの式です。また照射した光の振動数を\(ν\)、金属板Aの仕事関数を\(W\)とすると、前述の通り運動エネルギーとの関係は\(\displaystyle\frac{1}{2}mv_{max}^2=hν-W\)となります。そのため、以下の関係が成り立ちます。
- \(\displaystyle\frac{1}{2}mv_{max}^2=eV_0=hν-W\)
なお、1秒間で通過する電気量が電流の定義です。そのため、1秒間に金属から飛び出した電子の数を\(n\)とすると、一つの電子がもつ電気量\(e\)をかけることにより、以下のように光電流\(I\)を表すことができます。
- \(I=en\)
このように、光量子仮説を利用して光電効果を考えることにより、多くの現象を説明できるのです。
光電効果と光量子仮説の関係は重要
理由がわからない現象は物理で多く、理論として変であっても、実験によって証明されているのであれば受け入れる必要があります。その一つが光量子仮説であり、光は波だけでなく、粒子としての性質をもちます。
光を金属に当てることによって電子が飛び出す現象が光電効果です。単純な現象ではあるものの、アインシュタインが光量子仮説を提唱するまで、すべての物理学者が光電効果を説明できませんでした。
そこで、光と粒子の関係を学びましょう。公式を覚えるだけでなく、公式がもつ意味を理解する必要があります。光子がもつエネルギーは振動数(波長)に依存し、光の明るさは関係ありません。光の明るさというのは、光子の数に該当します。
量子力学の初歩が光電効果です。アインシュタインが光量子仮説を提唱してから量子力学が発展したのです。そこで光電効果が起こる原理を学び、光が粒子性をもつことでどのような現象が起こるのか理解しましょう。






