回路にコンデンサーを含むことは多く、どのようにコンデンサーの電気容量を計算すればいいのか学びましょう。電気容量を計算することによって、コンデンサーの電気量と電圧(電位差)の計算が可能になります。
コンデンサーの接続方法には並列接続と直列接続があります。接続方法によって、電気容量の計算方法が変わります。なお、電気容量の合計を合成容量といいます。
なお合成容量の計算をするとき、公式は覚えないようにしましょう。公式を暗記しても、応用問題を解けないケースが多いです。そこで公式の意味を学び、公式を作れるようになりましょう。そうすれば、すべての問題に対応できます。
公式の暗記ではなく、公式の意味を学ばなければいけない内容の一つがコンデンサーの合成容量です。そこで、どのように合成容量を計算すればいいのか解説していきます。
もくじ
コンデンサーの並列接続と直列接続の公式
回路には並列接続と直列接続があります。当然、コンデンサーを並列接続させることがあれば、直列接続させることもあります。
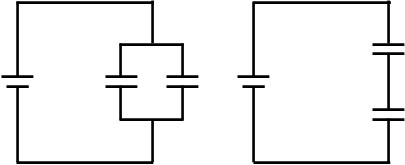
ただ複数のコンデンサーがある場合、計算が大変です。そこで、複数のコンデンサーを一つのコンデンサーとみなして計算しましょう。
なおコンデンサーの合成容量\(C\)を計算するとき、教科書に以下の公式が掲載されていることが多いです。
- 並列接続:\(C=C_1+C_2+C_3+…\)
- 直列接続:\(\displaystyle\frac{1}{C}=\displaystyle\frac{1}{C_1}+\displaystyle\frac{1}{C_2}+\displaystyle\frac{1}{C_3}+…\)
この計算により、コンデンサーの合成容量を得ることができます。
応用問題が出されると公式を利用できない
ただ、先ほどの公式を覚えてはいけません。公式を利用しても、応用問題では問題を解けないことが多いからです。
例えば直列接続で先ほどの公式を利用する場合、「コンデンサーに電荷の蓄積がない」という条件があります。つまり、電荷が貯まっているコンデンサーでは、先ほどの公式を利用して合成容量を計算することができません。
このように、条件が加わると利用できなくなるのがコンデンサーの合成容量に関する公式です。これが、公式を覚えても意味がない理由です。
そこで、公式を作れるようになりましょう。これにより、すべての回路についてコンデンサーの電気量を計算できるようになります。
電気量保存の法則とキルヒホッフの法則を利用して公式を作る
コンデンサーを複数含む回路の計算方法は決まっており、必ず以下の2つの法則を利用することによって式を作りましょう。
- 電気量保存の法則(または、電気量の合計)
- キルヒホッフの第二法則
これらの法則により、先ほどの公式を覚えなくても合成容量の計算が可能です。また、すべてのケースで電気量の計算が可能です。それでは、並列接続と直列接続に分けて計算してみましょう。
並列接続でのコンデンサーの合成容量
まず、コンデンサーが並列接続されている場面を考えましょう。起電力が\(V\)の電源に対して、コンデンサー1(電気容量\(C_1\))とコンデンサー2(電気容量\(C_2\))が並列接続されている場合、以下のように電気量を計算できます。
- \(Q_1=C_1V\)
- \(Q_2=C_2V\)
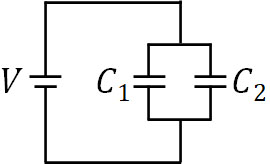
それでは、並列接続のコンデンサーについて、電気量の合計を計算しましょう。2つのコンデンサーは並列になっているため、コンデンサー1とコンデンサー2を一つのコンデンサーとみなす場合、2つのコンデンサーの電気量を足せばいいのは容易に想像できます。
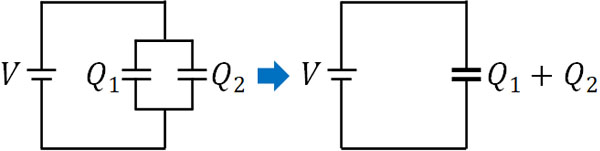
そのため、2つのコンデンサーの合成容量を\(C\)、電気量を\(Q=Q_1+Q_2\)とすると、以下の式を作れます。
\(Q=C_1V+C_2V\)
\(Q=(C_1+C_2)V\)
こうして、電気容量の合計(合成容量)は\(C=C_1+C_2\)になるとわかります。また、コンデンサーが増えても計算方法は同じなので、並列接続での合成容量は以下のようになります。
- \(C=C_1+C_2+C_3+…\)
前述の通り、公式として覚えるのではなく、回路の性質を利用して合成容量の計算式を作れるようになりましょう。
直列接続でのコンデンサーの合成容量
直列接続の場合についても、コンデンサーの合成容量に関する計算方法は同じです。以下のように、起電力が\(V\)の電源に対して、コンデンサー1(電気容量\(C_1\))とコンデンサー2(電気容量\(C_2\))が直列接続されている場面を考えましょう。
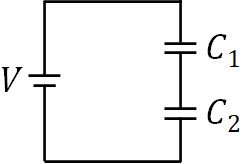
直列接続では、コンデンサー1とコンデンサー2に加わっている電圧が異なります。そのため、並列接続と同じ方法で計算することができません。そこで、電気量保存の法則を利用しましょう。
回路内で独立して存在している場所については、電源を利用して電流を通した後であっても、電気量の合計は前後で必ず同じになります。電源に接続する前、コンデンサーに蓄積されている電荷がゼロなのであれば、以下の独立部分では、電荷量の合計は必ずゼロです。
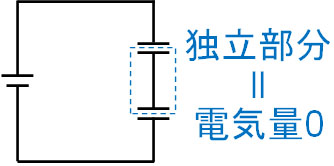
そのため電源につなぎ、2つのコンデンサーが荷電した場合であっても、電気量保存の法則により、電気量を合計するとゼロになります。つまり、コンデンサー1の電気量を\(Q_1\)、コンデンサー2の電気量を\(Q_2\)とすると以下の関係が成り立ちます。
\(-Q_1+Q_2=0\)
\(Q_1=Q_2\)
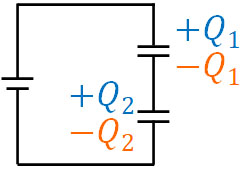
こうして、コンデンサー1とコンデンサー2の電気量は同じであるとわかりました。
次に、キルヒホッフの第二法則を利用して式を作りましょう。回路を一周させる場合、必ず電圧はゼロになります。コンデンサー1に加わる電圧を\(V_1\)、コンデンサー2に加わる電圧を\(V_2\)として、以下の式を作りましょう。
\(V+(-V_1)+(-V_2)=0\)
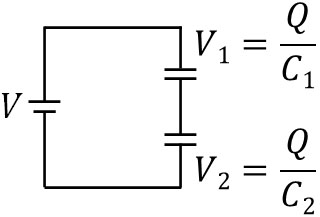
なおコンデンサーの公式より、\(Q=CV\)であるため、\(V=\displaystyle\frac{Q}{C}\)です。そこで、それぞれのコンデンサーが保有する電気量を\(Q_1\)、\(Q_2\)とすると、\(Q_1=\displaystyle\frac{Q}{C_1}\)であり、\(Q_2=\displaystyle\frac{Q}{C_2}\)です。
また前述の通り、2つのコンデンサーはそれぞれ保有する電気量が同じになります。そのため、独立部分を足すと電気量が0になります。
合計すると電気量が0であるため、コンデンサーの独立部分を無視しましょう。そうすると、電気量\(Q\)が蓄積している2つのコンデンサーについて、以下のように「電気量\(Q\)が蓄積している1つのコンデンサー」とみなすことができます。
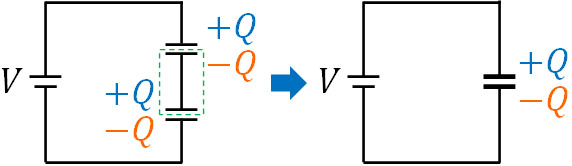
そこで合成コンデンサーの電気容量(合成容量)を\(C\)とするとき、コンデンサーに蓄積される電気量は\(Q\)であり、電圧は\(V\)です。そのため、電源に着目すると\(V=\displaystyle\frac{Q}{C}\)の式を作れます。そこで、以下のように計算しましょう。
\(V+(-V_1)+(-V_2)=0\)
\(V=V_1+V_2\)
\(\displaystyle\frac{Q}{C}=\displaystyle\frac{Q}{C_1}+\displaystyle\frac{Q}{C_2}\)
\(\displaystyle\frac{Q}{C}=Q\left(\displaystyle\frac{1}{C_1}+\displaystyle\frac{1}{C_2}\right)\)
\(\displaystyle\frac{1}{C}=\displaystyle\frac{1}{C_1}+\displaystyle\frac{1}{C_2}\)
このように計算すると、コンデンサーに電荷が存在していない場合、直列接続での合成容量\(C\)を得ることができます。
電荷をもつ場合、直列接続の公式を利用できない
なお前述の通り、コンデンサーに電荷がある場合、直列接続での公式を利用できません。一方、ここまで解説した方法であれば、コンデンサーに電荷が存在する場合であっても電気量や電圧の計算できます。
例えば以下のように、10Cと4Cに荷電しているコンデンサーであれば、独立部分の合計は-6Cになります。

荷電していない状態の場合、独立部分の電荷を合計するとゼロになります。一方でコンデンサーに荷電がある場合、独立部分の電荷を足すと、当然ながら電荷はゼロにはなりません。
電気量保存の法則により、電荷を合計すると常に一定になります。上図の例だと、常に独立部分の電荷は-6Cになります。そのため先ほどのように、コンデンサーの独立部分を無視して、一つのコンデンサーとみなすことができません。
それでは、コンデンサーに電荷のある状態でスイッチを入れる場合について、電気量を計算してみましょう。先ほどの回路について、電気量保存の法則を利用すると、以下の式を作れます。
\(-Q_1+Q_2=-6\)
\(Q_2=Q_1-6\)
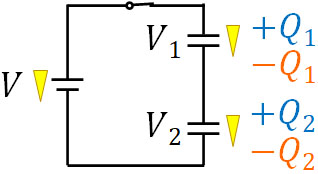
また、2つのコンデンサーの電気容量が両方とも\(C\)であるケースを考えましょう。この場合、キルヒホッフの法則より、以下の式を作れます。
\(V+(-V_1)+(-V_2)=0\)
\(V=\displaystyle\frac{Q_1}{C}+\displaystyle\frac{Q_2}{C}\)
\(V=\displaystyle\frac{Q_1}{C}+\displaystyle\frac{Q_1-6}{C}\)
\(V=\displaystyle\frac{2Q_1-6}{C}\)
\(VC=2Q_1-6\)
\(2Q_1=VC+6\)
\(Q_1=\displaystyle\frac{VC}{2}+3\)
また\(Q_2=Q_1-6\)であるため、\(Q_2=\displaystyle\frac{VC}{2}-3\)です。こうして、それぞれのコンデンサーの電気量を計算することができました。合成容量を利用しなくても、電気量を計算できるのです。
電気量保存の法則とキルヒホッフの法則を利用する場合、電荷をもつ場合であっても計算できます。すべてのケースで問題を解けるようになるため、公式の暗記ではなく、電気量保存の法則とキルヒホッフの法則を利用して式を作れるようになりましょう。
公式を暗記せず、式を作れるようにする
コンデンサーの合成容量を計算するとき、公式の暗記は避けましょう。公式を暗記しても、利用できない場面が多いからです。
そうではなく、回路を利用して式を作れるようになりましょう。コンデンサーの並列接続では、電気量の足し算が可能です。それに加えて、キルヒホッフの法則を利用して式を作りましょう。
コンデンサーの直列接続についても考え方は同じです。電気量保存の法則とキルヒホッフの法則を利用して式を作りましょう。この方法であれば、コンデンサーが荷電している状態であっても式を作れます。
物理では公式を覚えても意味がないケースが多く、その一つがコンデンサーの合成容量です。そこでコンデンサーが複数ある場合、合成容量の意味を理解したうえで、電気量保存の法則とキルヒホッフの法則を活用しましょう。






