数学を学ぶとき、交換法則と結合法則について教えてもらうことがあります。小学校や中学校などで習うのが交換法則と結合法則です。
交換法則と結合法則は足し算と掛け算で成り立ちます。引き算と割り算では、交換法則と結合法則は成り立ちません。ただ、引き算は足し算に、割り算は掛け算に変換できます。つまり、すべての計算でこれらの法則を利用できます。
数学でこれらの法則を理解するのは重要です。交換法則と結合法則を理解することで、あらゆる計算を行えるようになります。中学生以上の数学では割り算を利用することがなくなりますが、交換法則や結合法則によってこの理由を理解することもできます。
そこで交換法則と結合法則をどのように考え、応用すればいいのか解説していきます。
もくじ
交換法則と結合法則の概要
小学校または中学校で学ぶ交換法則と結合法則について、どのような内容になっているのでしょうか。それぞれを簡単に記すと、以下のようになります。
- 交換法則:数字を入れ替えても同じ答えになる法則
- 結合法則:かっこの場所を変えても同じ答えになる法則
交換法則と結合法則については、両方とも非常に多くの場面で利用される法則であり、数学で計算問題を解くときは必須の知識です。これらの法則は足し算と掛け算に利用されます。ただ実際には、引き算と割り算にも応用することができます。
つまり、すべての計算で交換法則と結合法則を利用できます。そのため利便性が高く、高校や大学、さらには社会人で数学計算をする人を含め、すべての人で交換法則が有効です。
数字の入れ替えで同じ答えになる交換法則
交換法則では、数字を入れ替えたとしても答えが同じになります。足し算(加法)では、交換法則が成り立ちます。
例えば、以下のようになります。
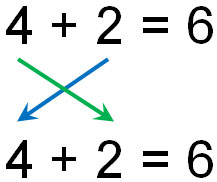
どのように順番を入れ替えても問題なく、これを加法の交換法則といいます。
同じことは掛け算(乗法)にもいえます。足し算だけでなく、掛け算でも交換法則が成り立ちます。以下のように、掛け算では数字を入れ替えたとしても答えは同じです。
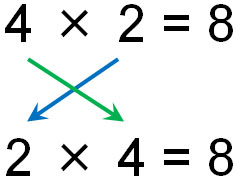
どのように掛け算をしても問題なく、これを乗法の交換法則といいます。
引き算と割り算では交換法則が成り立たない?
ただ、引き算(減法)と割り算(除法)では交換法則が成り立たないといわれています。実際に数字を交換して計算してみましょう。
例えば、引き算について数字を入れ替えると以下のようになります。
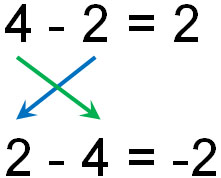
このように、答えが違います。一方の式では答えが2となり、もう一方の式では-2となります。異なる数字の引き算になるため、当然ながら答えは違ってしまいます。引き算で交換法則が成り立たないといわれるのは、こうした理由があります。
同じことは割り算にもいえます。割り算の場合、以下のようになります。
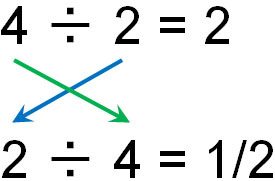
割り算で交換法則を利用すると、このように答えが変わります。そのため、割り算で交換法則は成り立ちません。
符合を直し、負の数にすると交換法則が成り立つ
足し算と掛け算でのみ交換法則が成り立つとなると、利用場面が限られるので意味がないように思ってしまいます。ただ、小学校の算数や中学校の数学で学ぶ交換法則は非常に重要な法則です。
なぜ、足し算と掛け算でのみ適用されるにも関わらず、交換法則は重要なのでしょうか。それは、引き算を足し算に変えることで、交換法則が成立するようになるからです。割り算についても、掛け算に直すことで交換法則が成り立ちます。
足し算と引き算は同じです。引き算は足し算に直すことができます。例えば、以下はすべて同じ計算式であり、同じ答えです。
- \(4-2=2\)
- \(4+(-2)=2\)
正の数と負の数を学べば、足し算と引き算は同じと理解できます。
前述の通り、足し算であれば交換法則が成り立ちます。そこで引き算を「負の数の足し算」に直すことで、交換法則が成立します。
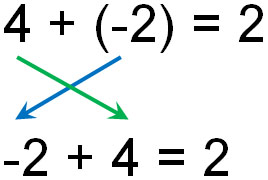
重要なのは、負の数であっても交換法則が成り立つという事実です。先ほど、引き算は交換法則が成り立たないと解説しました。ただ実際には、引き算を足し算に変えることで交換法則が成り立つため、引き算であっても加法の交換法則を利用できます。
・割り算で分数を使い、交換法則を利用する
同じことは割り算にもいえます。割り算を掛け算に直すことで、乗数の交換法則を利用できるようになります。
どのようにして、割り算を掛け算に直すのでしょうか。これには分数を利用します。逆数を使うことで、割り算を分数の掛け算に直します。以下のように、割り算は分数の掛け算でもあります。
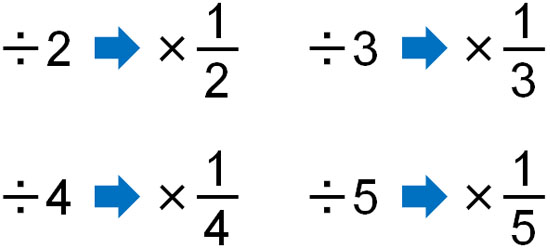
前述の通り、掛け算では交換法則が成り立ちます。以下のように、分数であっても掛け算では答えが同じです。
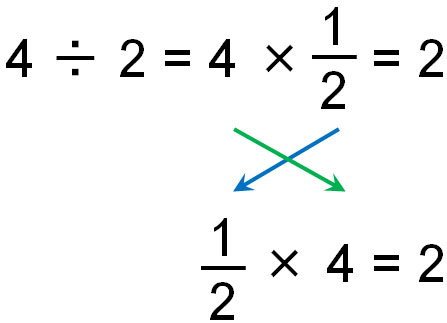
引き算を足し算に直す場合、プラスとマイナスの符合を変えるだけでいいです。ただ割り算の場合、分数に直さなければいけません。そのためひと手間が必要です。ただいずれにしても、割り算であっても交換法則を利用できます。
かっこの場所を変えられる結合法則
交換法則を学ぶとき、同時に習う法則として結合法則があります。結合法則とは、どのような法則なのでしょうか。
かっこの場所を自由に変えられるのが結合法則です。交換法則と同じように、結合法則も足し算(加法)と掛け算(乗法)のみ成立します。以下のように、足し算ではかっこの場所を変えても答えは同じです。
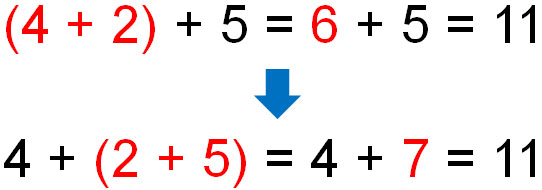
算数や数学では、かっこの中を先に計算するというルールがあります。足し算では、どこにかっこを付けても問題ありません。
同じように、掛け算でも結合法則が成り立ちます。
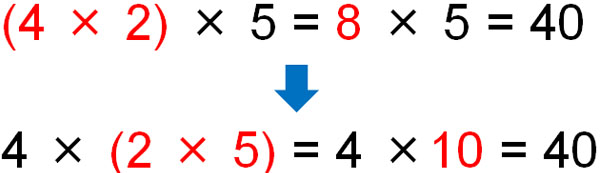
なぜ、結合法則が成り立つのでしょうか。それは、かっこがあってもなくても意味が同じだからです。以下のように、かっこを消しても答えは同じです。
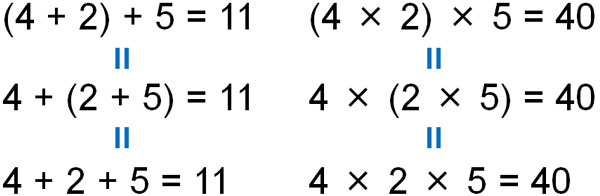
かっこがあってもなくても関係ないため、どこにかっこを付けても答えは同じです。結合法則というのは、当たり前のことを法則にしているにすぎません。
好きな場所を計算できる法則が結合法則
結合法則というのは、要は「どこから先に計算してもいい」という法則です。例えば掛け算をするとき、数字の順番を変えて計算したことが誰でもあるはずです。例えば、以下の計算をどのようにするでしょうか。
- \(2×6×13\)
左から順に計算すると、以下のようになります。
- \(\color{red}{2×6}×13=\color{red}{12}×13=156\)
\(12×13\)の計算をする必要があり、計算が難しくなります。そこで結合法則を利用し、数字の順番を変えましょう。例えば、\(2×6×13\)ではなく、\(6×13×2\)に式を変えます。この場合、以下のようになります。
- \(\color{red}{6×13}×2=\color{red}{78}×2=156\)
このように、計算が簡単になります。2桁同士の数字の掛け算をするよりも、桁数の少ない数字を掛けるほうが計算ミスは少なくなります。
引き算と割り算は符合を変えて公式が成立する
足し算や掛け算の式に有効なのが結合法則です。引き算と割り算に適用できないのは、交換法則と同じです。例えば、引き算ではかっこの場所を変えることで以下のように答えが変わります。
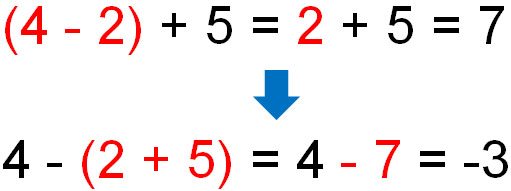
式にかっこがある場合、最初にかっこの中を計算しなければいけません。そのため引き算があると、結合法則によって答えが変わります。
同じことは割り算にも起こります。以下のように、かっこの場所が変わることで答えが変化します。

引き算と割り算については、結合法則が成り立ちません。
・足し算または掛け算に直して計算する
ただ、実際には引き算や割り算があっても問題ありません。交換法則と同じように、引き算は足し算に、割り算を掛け算に直すことができます。以下のようになります。
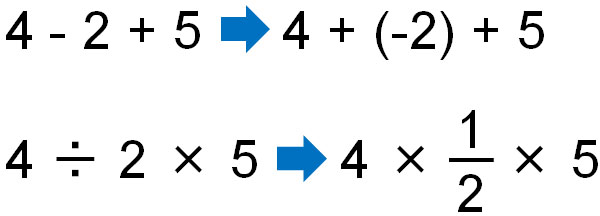
足し算または掛け算の計算式に直すことができ、結合法則が成り立つようになります。どこにかっこを付けても同じ答えです。つまり、どの場所から先に計算をしてもいいです。
結合法則では、一般的に引き算と割り算で利用できないといわれています。しかし、足し算または掛け算の式に直すことで、結合法則が成り立つようになります。そのため結合法則はすべての計算で利用できる法則です。
数学で割り算を利用せず、逆数(分数)の掛け算を使う
それでは、なぜ小学校の算数や中学校の数学を含め、交換法則と結合法則を理解する必要があるのでしょうか。これは、より簡単に計算をするために必須だからです。特に割り算の計算では、結合法則と交換法則の理解が重要です。
引き算を足し算に直すとき、やり方は簡単です。足し算にした後、マイナスの数にするだけです。以下のようになります。
- \(2\color{red}{-3}=2\color{red}{+(-3)}\)
一方で割り算については、そのままの状態では計算できません。割り算を掛け算にするためには、分数の掛け算に直す必要があります。逆数を利用することで、形を変えなければいけません。
- \(2\color{red}{÷3}=2\color{red}{×\displaystyle\frac{1}{3}}\)
掛け算だけの式にすることで、どこから計算できます。
結合法則と交換法則が成り立たないことから、中学以上の数学で割り算を使うことはありません。中学校や高校の数学を含め、数学では割り算を使わないのです。そうではなく、割り算を分数に直した後に計算します。
また割り算の場合、割り切れないケースは非常に多いです。一方で分数であれば、割り切れない場合であっても答えを出すことができます。割り算は利便性が悪く、数学での利用場面はほぼないと理解しましょう。
なぜ、中学以上の数学で全員が割り算を掛け算に直すのかの理由としては、交換法則と結合法則を利用できるようにすることが挙げられます。そのほうが圧倒的に計算しやすくなり、計算ミスが少なくなります。
練習問題:プラスとマイナスの数の交換法則と結合法則
Q1. 次の計算をしましょう
- \((6÷15)×5\)
- \(-4÷3÷6×15\)
A1. 解答
足し算と引き算については、交換法則と結合法則を利用するとき、特にトラブルなく問題を解くことができます。一方で割り算が含まれる場合、分数の掛け算に直す必要があります。そこで逆数を利用し、分数にしましょう。
(a)
\((6\color{red}{÷15})×5\)
\(=(6\color{red}{×\displaystyle\frac{1}{15}})×5\)
\(=6×\displaystyle\frac{1}{3}=2\)
割り算では、必ず分数の掛け算に直します。その後、この計算では先に「\(\displaystyle\frac{1}{15}×5=\displaystyle\frac{1}{3}\)」を計算しています。「\(6×\displaystyle\frac{1}{15}\)」よりも計算が簡単だからです。
(b)
\(-4÷3÷6×15\)
\(=-4×\displaystyle\frac{1}{3}×\displaystyle\frac{1}{6}×15\)
\(=\color{red}{-4×\displaystyle\frac{1}{6}}×\color{blue}{\displaystyle\frac{1}{3}×15}\)
\(=\color{red}{-\displaystyle\frac{2}{3}}×\color{blue}{5}\)
\(=-\displaystyle\frac{10}{3}\)
最初、割り算を分数の掛け算に直します。その後、交換法則と結合法則を利用することで、計算しやすいように数字を入れ替えています。
\(-4×\displaystyle\frac{1}{3}\)や\(\displaystyle\frac{1}{6}×15\)では計算が難しいです。また、分数同士の掛け算も難しいです。
一方で\(-4 × \displaystyle\frac{1}{6}\)や\(\displaystyle\frac{1}{3}×15\)であれば、数字を小さくできるので計算が簡単です。掛け算のみの式では、自由に数字を移動させることができます。このようにして、交換法則と結合法則を利用します。
法則の定義を学び、公式で利用する
数学にはいくつかの法則があります。その法則の一つが交換法則と結合法則です。なぜ、法則を理解する必要があるのでしょうか。それは、法則を利用することで式の計算が容易になり、計算ミスを少なくできるからです。
数学で重要な法則としては、全員が利用するものに交換法則と結合法則があります。小学校で習う算数でも、全員が交換法則と結合法則を利用しています。
ただ、法則を数学の公式で利用するにはルールや定義を理解しなければいけません。交換法則と結合法則は足し算または掛け算だけの式でのみ有効です。そこで引き算や割り算がある場合、足し算または掛け算に直しましょう。引き算を直すのは簡単ですが、割り算では分数に直さなければいけないことに注意しましょう。
また交換法則と結合法則を理解すれば、中学生以上の数学で割り算を利用する人がいない理由を理解できます。割り算は利便性が悪いです。必ず逆数を取って分数の掛け算に直した後、計算するようにしましょう。






