中学数学で相似を学びます。相似の分野で重要な内容の一つが中点連結定理です。三角形の中点を利用することで、辺の長さを計算できるようになります。
また三角形だけでなく、台形の辺の長さを計算したり、平行四辺形の証明をしたりすることもできます。台形や平行四辺形と他の図形にも応用できる考え方が中点連結定理です。
中点連結定理を理解することで辺の長さを計算できるようになれば、他のパターンについても計算できるようになります。中点同士を結ぶケースでなかったとしても、相似の性質を利用することで辺の長さを出せるようになるのです。
そこで、ここでは相似で重要な中点連結定理について解説し、中点連結定理の逆や証明、応用問題の解き方を解説していきます。
もくじ
平行線で成り立つ中点連結定理とは何か
中点連結定理という言葉をみると、難しそうに思えてしまいます。ただ三角形の相似について学んだあとであれば、中点連結定理は非常に簡単です。
まず、中点連結定理では三角形を考えます。三角形で2つの中点を取ります。その場合、以下のような図形になります。
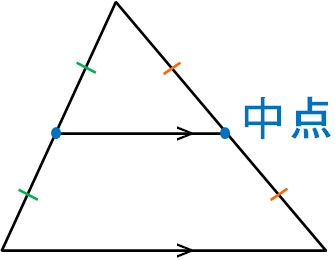
この場合、以下の2つが成り立ちます。
- 底辺と中点を結ぶ線は平行
- 底辺の長さは、中点を結ぶ線の長さの2倍
これが中点連結定理です。中点連結定理とは、要は「相似比が1:2の三角形」と理解すればいいです。三角形の中点を結ぶことによって、相似の三角形を作ることができ、相似比が1:2になるというわけです。
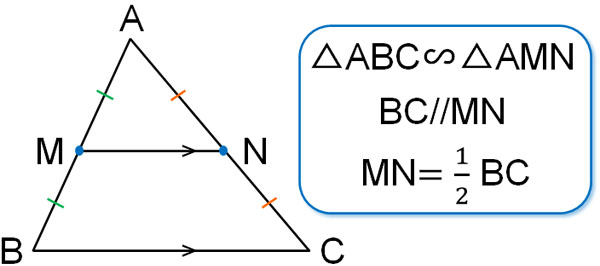
辺の中点なので、相似比が1:2になることは容易に理解できます。この性質が中点連結定理です。
証明で中点連結定理が成り立つ理由を説明
それでは、なぜ中点連結定理が成り立つのでしょうか。この理由を証明してみましょう。中点なので、辺の比は必ず1:2になると分かります。そのため、以下のように証明できます。
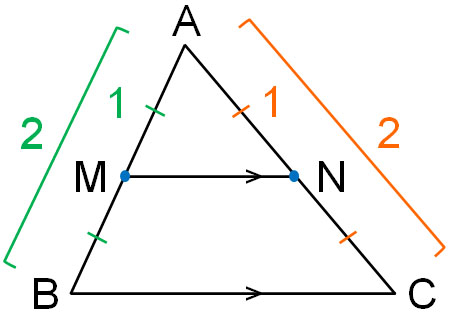
- △ABCと△AMNにおいて
- ∠BAC=∠MAN:共通の角 – ①
- AB:AM=2:1、MはABの中点 – ②
- AC:AN=2:1、NはACの中点 – ③
- ①、②、③より、2組の辺の比とその間の角が等しいため、△ABC∽△AMN
こうして、△ABC∽△AMNであることを証明できました。また△ABC∽△AMNの相似比は2:1なので、MNの長さはBCの2分の1になることが分かります。
また相似図形の場合、対応する角度は同じです。つまり、∠ABC=∠AMNです。同位角が等しい場合、2つの線は平行です。そのため、BC//MNです。こうして、BCとMNが平行であることも証明できました。
中点連結定理の逆も成り立つ
重要なのは、中点連結定理の逆も成り立つという事実です。つまりBC//MN、かつ\(MN=\displaystyle\frac{1}{2}BC\)の場合、点Mと点Nは辺の中点です。以下のように証明できます。

- △ABCと△AMNにおいて
- ∠BAC=∠MAN:共通の角 – ①
- ∠ABC=∠AMN:平行線の同位角は等しい – ②
- ①、②より、2組の角がそれぞれ等しいため、△ABC∽△AMN
また\(MN=\displaystyle\frac{1}{2}BC\)なので、△ABC∽△AMNの相似比は2:1です。この事実から、以下となることが分かります。
- \(AM=\displaystyle\frac{1}{2}AB\)
- \(AN=\displaystyle\frac{1}{2}AC\)
そのため点Mと点Nは辺の中点です。こうして、中点連結定理の逆が成立することが分かりました。
中点でなくても、相似比から辺の長さを計算できる
ここまで、三角形の中点について解説してきました。ただ重要なのは、中点連結定理の性質は中点でなくても利用できることです。
例えば三角形について、1:2の割合で以下のように点を取るとします。
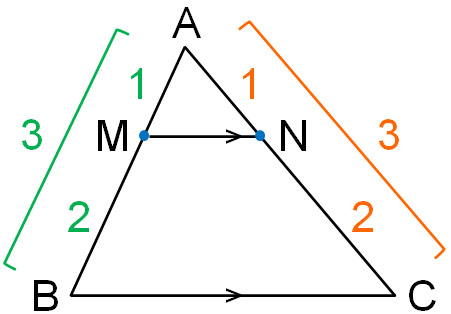
この場合、BC//MN、かつ\(MN=\displaystyle\frac{1}{3}BC\)となります。この理由については、先ほど中点連結定理の証明をした方法と同じやり方にて説明することができます。中点でなかったとしても、中点連結定理の性質は成立します。
相似の図形では、各辺の相似比はすべて同じです。今回の場合、△ABC∽△AMNの相似比は3:1です。そのため、一つの辺の長さが分かれば他の辺の長さについても計算できるようになります。例えば、MNの長さが3cmの場合、MN:BC=1:3のため、BCの長さは9cmです。
また2つの線が平行な場合、辺の比はすべて同じになります。例えば先ほどの図形であれば、AM:MB=1:2です。また、AN:NC=1:2です。

例えばAMの長さが0.5cmの場合、MBの長さは1cmです。ANの長さが0.7cmの場合、NCの長さは1.4cmです。相似の三角形では、底辺が平行な場合だと、辺の比に応じて長さの計算が可能です。
平行線では、線の長さの比は同じ
それでは、これらの内容を理解した後に応用問題を解けるようにしましょう。以下の図形で\(l//m//n\)の場合、\(x\)の値はいくらになるでしょうか。

どのようにして、この問題を解けばいいのでしょうか。この状態のままでは、\(x\)をどのようにして計算すればいいのか分かりません。そこで、以下のように線を移動させてみましょう。
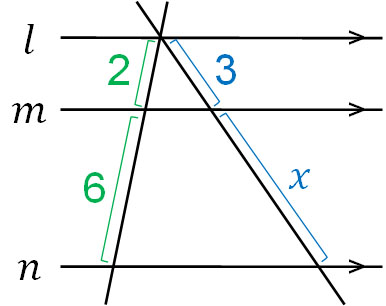
線を移動させたとしても、辺の長さは変わりません。また、このように線を移動させることによって、三角形を作ることができます。底辺が平行な三角形なので、先ほど説明した相似図形の性質を利用できます。
以下の比例式を作ることによって、\(x\)の値を計算できます。
- \(2:6=3:x\)
この比例式を解くと、以下のようになります。
\(2x=6×3\)
\(x=9\)
こうして、\(x\)の値は9と分かります。
台形の辺の長さを計算する
また相似や中点連結定理を学ぶとき、応用問題として台形の辺の長さを計算させる問題が出されることがあります。例えば、以下の図形で\(x\)の長さはいくらでしょうか。
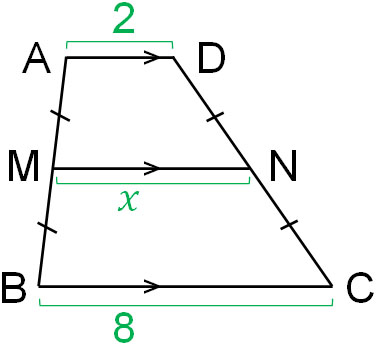
AD//MN//BCの図形です。また、AM=MB、DN=NCであり、中点連結定理を利用できます。ただ三角形ではなく、台形なのでどのように考えれば問題を解けるのか、ここままでは分かりません。
そこで、以下のような線を引きましょう。
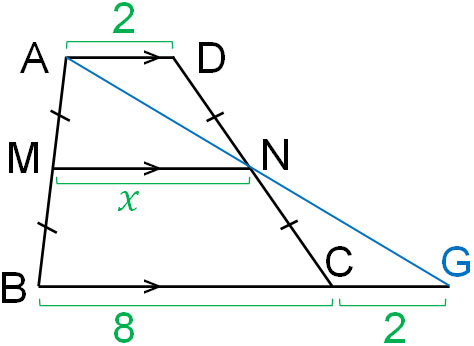
このとき、△ADNと△GCNは合同です。合同である証明は省きますが、「1組の辺とその両端の角がそれぞれ等しい」の定理を利用することで、2つの三角形が合同だと分かります。
△ADNと△GCNは合同なので、AD=CG=2です。つまり、BGの長さは10です。また△ABGは三角形であり、MとNはそれぞれの辺の中点です。そのため、中点連結定理を利用することによってMNの長さを計算できます。
前述の通り、BGの長さは10です。そのため、\(x\)の長さは5と分かります。
平行線をもつ台形の問題では、そのままの状態では問題を解くことができません。そこで線を移動させたり、新たな線を引いたりすることによって、三角形を作るようにしましょう。そうすれば、中点連結定理や相似の性質を利用することで辺の長さを出せるようになります。
四角形で中点連結定理を使うと平行四辺形になる
なお中学数学では、中点連結定理を利用することによって、平行四辺形になる証明を行う問題が出されることもあります。以下のような図形が提示され、四角形の中点をそれぞれ結ぶことで平行四辺形を作れることを証明するのです。
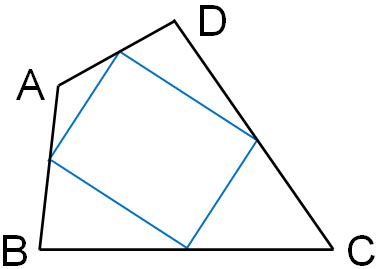
平行四辺形を満たす条件はいくつかあります。以下になります。
- 2組の対辺がそれぞれ平行
- 2組の対辺の長さが等しい
- 2組の対角がそれぞれ等しい
- 対角線がそれぞれの中点で交わる
- 1組の対辺が平行、かつ長さが等しい
このうち、平行四辺形の証明ではほぼ「1組の対辺が平行、かつ長さが等しい」を使います。この証明問題についても、「1組の対辺が平行、かつ長さが等しい」を利用することで平行四辺形であることを証明することになります。
数学の図形問題では、解き方を覚えなければいけません。そこで、どのように考えて証明すればいいのか理解しましょう。まず、以下のようにACとなる対角線を引きます。
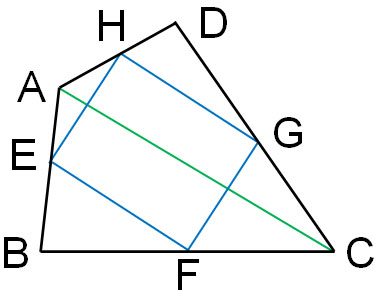
引く対角線はACでもBDでも、どちらでもいいです。やり方はどちらも同じですが、今回は対角線ACによって説明していきます。
次に、2つの三角形に着目しましょう。以下の三角形になります。

HはADの中点なので、AH=HDです。またGはDCの中点なので、DG=GCです。三角形の2つの中点を結んでいるため、中点連結定理より以下のようになります。
- HG//AC – ①
- HG=\(\displaystyle\frac{1}{2}\)AC – ②
同様に、反対側の三角形を考えてみましょう。
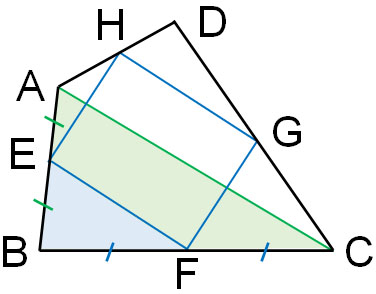
EはABの中点なので、AE=EBです。またFはBCの中点なので、BF=FCです。三角形の2つの中点を結んでいるため、中点連結定理より以下のようになります。
- EF//AC – ③
- EF=\(\displaystyle\frac{1}{2}\)AC – ④
①と③より、HG//EFです。また②と④より、HG=EFです。「1組の対辺が平行、かつ長さが等しい」なので、平行四辺形であると証明できました。
練習問題:三角形の中点連結定理と相似
Q1. AB//CD//EFのとき、\(x\)の値を計算しましょう
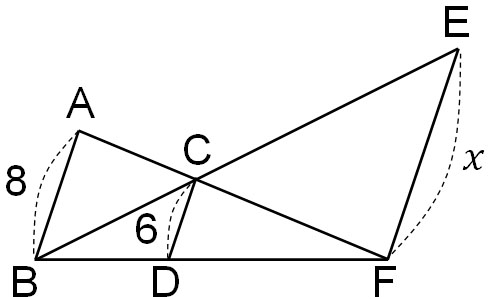
A1. 解答
△ABFと△CDFに着目すると、2つの三角形は相似です。そのため、以下のような辺の比になることが分かります。
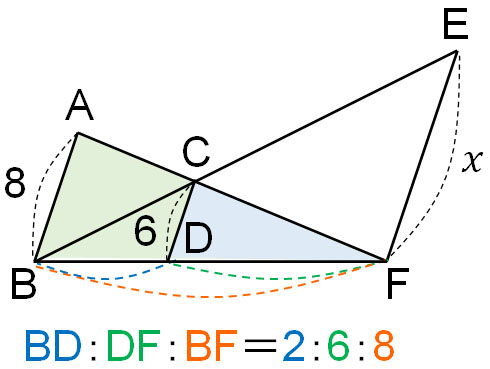
BDやDF、BFについて、具体的な辺の長さは分かりません。ただ、辺の比は分かります。相似比が分かれば、\(x\)の値を出すことができます。
次に△BDCと△BFEに着目しましょう。2つの三角形は相似です。また、△BDCと△BFEの相似比は辺の比から2:8(正確には1:4)と分かります。そのため、以下の比例式を作れます。
- \(2:8=6:x\)
この式を解くと、\(\)になります。
\(2x=6×8\)
\(x=24\)
Q2. AD//BCの台形について、MとNは辺の中点です。以下の図形でAD=6、BC=8のとき、POの長さを求めましょう。
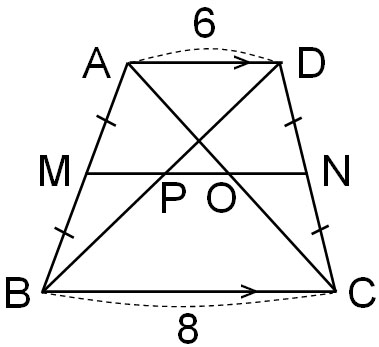
A1. 解答
台形の中点連結定理については、先ほど計算方法を述べました。MNの長さは以下の方法によって計算できます。
- \((8+6)×\displaystyle\frac{1}{2}=7\)
MNの長さは7です。またMとNは中点なので、PはBDの中点です。同じように考えると、OはACの中点です。
まず、PNの長さを出してみましょう。BCの長さは8なので、中点連結定理よりPNの長さは4です。つまり、MPの長さは3です。同じように考えると、中点連結定理よりMOの長さは4です。つまり、ONの長さは3です。
MP=3、ON=3、MN=7なので、POの長さは1です。
- \(7-3-3=1\)
平行な線の長さを計算する
三角形の2つの中点を利用することで、辺の長さを計算する方法として中点連結定理があります。中点連結定理では、2本の線(底辺および中点を結ぶ線)が平行であり、相似比は1:2になります。
重要なのは、中点に限らず相似比を利用して辺の長さを計算できることです。2本の線が平行な場合、辺の長さの比は相似比と同じです。
また、中点連結定理と相似の考え方は三角形だけに利用できるわけではありません。台形であっても、これらの性質を利用して辺の長さを計算できます。また中点連結定理を利用することで、四角形の中に平行四辺形を作れる理由を証明できます。
2本の線が平行である必要があるため、特殊な条件で利用できる計算方法です。ただ数学では中点連結定理が頻繁に出題されるため、相似を用いた辺の長さの計算方法を理解しておきましょう。