中学生では球の体積と表面積を出す計算を学びます。公式を覚える必要があり、公式を利用することで球の体積と表面積の計算方法を理解できます。
球の体積と表面積を出す公式は少し複雑です。また、なぜこの公式になるのか理由を解説するためには、高校数学の積分を学ばなければいけません。そのため内容は難しく、公式が成り立つ理由をここで詳しく解説することはしません。
その代わり、公式を利用することで、どのように球の体積と表面積を計算すればいいのか解説していきます。
数学の計算問題としては、球は出題頻度が低いです。それにも関わらず、公式を覚えなければいけない分野です。そこで、計算方法を理解するようにしましょう。
もくじ
球の体積を出す公式での求め方
数学では、球の体積を計算しなければいけない問題が出されることがあります。球は私たちにとって身近であり、スポーツでは多くの人が球を使います。例えばテニスやサッカー、バスケットボール、バレーボールでは球を使います。
以下の立体を数学では球といいます。

これら球の体積を計算するためには、公式を利用します。公式を覚えていない場合、球の体積を出すことはできません。以下が球の体積を出す公式です。

数字をこの公式に代入すれば、球の体積を出すことができます。
円柱と球の体積の関係
球にはユニークな性質があります。円柱の中に球がぴったり入る場合、球の体積は円柱の\(\displaystyle\frac{2}{3}\)になるという特徴があります。

この性質を利用することで、球の体積を出すことができます。
球の半径をrとします。その場合、円柱の高さは2rです。円柱の体積は、底面積と高さを掛けることで計算できます。そのため、球の体積は以下のようになります。

球の体積は公式を覚えていなければ計算できません。ただ、円柱の体積に2/3を掛けると、球の体積になることを理解すれば公式を導き出すことができます。
円錐・球・円柱の体積は相互関係がある
ちなみに、円錐と球、円柱はそれぞれ関係しています。円錐の体積は円柱の1/3になります。一方で球の体積は、円柱の2/3になります。
つまり、それぞれの体積比は以下のようになります。
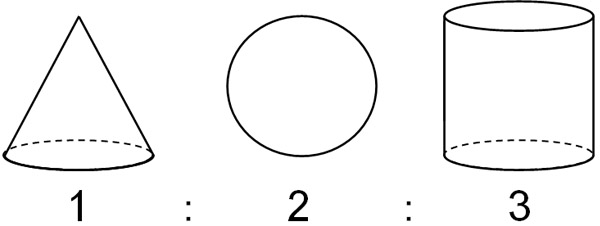
中学数学の計算をするとき、円錐(または角錐)の公式は必ず覚えなければいけません。角錐・円錐の体積を問う問題は頻繁に出されます。一方で円錐に比べると、球の体積を出す公式は重要ではありません。
ただ忘れてしまったとしても、以下の関係にあることを覚えておけば球の公式を作ることができます。
- 円錐:球:円柱=1:2:3
円柱に1/3を掛けることで、円錐の体積になります。このとき、円錐の体積の2倍が球です。また、円柱の体積に対して2/3を掛けると球の体積になります。
球の表面積を出す公式での求め方
球の体積を出す公式があるのと同じように、球の表面積を出す公式も存在します。体積の公式と同様に、球の表面積を出すときは公式を覚えていなければ計算することができません。
球の表面積を出す公式は以下になります。

球の表面積を計算したい場合、この公式に数字を代入するようにしましょう。
円柱の側面積と球の表面積の関係
ただ球の表面積の公式を覚えるのは大変です。球の体積と同じように、使用頻度は低いです。どのようにして、この公式を理解すればいいのでしょうか。
球の表面積についてもユニークな特徴があります。円柱の中に球がぴったり入る場合、球の表面積は円柱の側面積と同じになるという性質があります。
半径をrとすると、円柱の側面積の横の長さは\(2πr\)です。つまり円の直径が2rであり、これに円周率を掛けることで、円周(長方形の横の長さ)を出すことができます。一方で円柱の高さは2rです。

もし球の表面積の公式を忘れてしまったとしても、円柱の側面積と同じになることを知っていれば、公式を導き出すことができます。
練習問題:球の体積と表面積
Q1. 次の半球の体積と表面積を計算しましょう。なお、円周率は\(π\)とします。
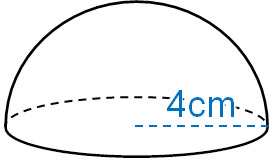
A1. 解答
・半球の体積
半球なので、体積は球の半分です。球の体積を出す公式に当てはめると、以下のように\(24π\)cm3になります。
- \(\displaystyle\frac{3}{4}π×4^3×\displaystyle\frac{1}{2}=24π\)
・半球の表面積
表面積は球の半分です。表面積の公式に当てはめると、以下のように計算できます。
- \(4π×4^2×\displaystyle\frac{1}{2}=32π\)
また、半球の断面図の面積を加えなければいけません。円の面積の公式に当てはめると、以下のように計算できます。
- \(4×4×π=16π\)
面積の合計は以下のように\(48π\)cm2になります。
- \(32π+16π=48π\)
公式を利用して球の問題を解く
中学数学で学ぶ分野の一つが球の体積と表面積です。数学の問題としては出題頻度が少ないものの、公式を覚えていなければ問題を解けません。
数学の計算問題で何度も球の公式を使うことはないため、公式を忘れてしまいがちです。そこで、球の公式の出し方を理解するようにしましょう。忘れてしまったとしても、円柱の体積や側面積を出す公式から、球の公式を作ることができます。
- 球の体積:円柱の体積の2/3
- 球の表面積:円柱の側面積と同じ
この性質を覚えていれば、球の公式をいつでも作ることができます。その後、公式を利用して球の体積と表面積を出すようにしましょう。






