電流が流れることによって仕事が行われます。そのため回路にコンデンサーがある場合、コンデンサーに電気量が蓄積することによって、コンデンサーはエネルギーをもつことになります。このエネルギーを静電エネルギーといいます。
コンデンサーがエネルギーをもつためには、電源が仕事をしなければいけません。仕事とエネルギーは意味が同じであり、仕事されることによってエネルギーが増えるのです。
なお電源による仕事が行われるとき、ジュール熱が発生します。すべての仕事がエネルギーの蓄積に利用されるわけではなく、ジュール熱としてエネルギーが外部へ放出されるのです。
それでは、静電エネルギーや仕事、ジュール熱をどのように計算すればいいのでしょうか。ここでは、コンデンサーの静電エネルギーについて解説していきます。
もくじ
コンデンサーによる仕事は\(QV\)ではない
充電により、コンデンサーには電荷が蓄積します。つまり、コンデンサーはエネルギーを保有しているとわかります。電荷をもつコンデンサーに対して電球をつけると、電球は光ります。これは、コンデンサーがもつエネルギーが光エネルギーへと変換されるからです。
それでは、コンデンサーがもつ電気量を\(Q\)、電位差(電圧)を\(V\)とすると、コンデンサーが行う仕事は\(W=QV\)なのでしょうか。
実は、コンデンサーによる仕事は\(W=QV\)によって計算することができません。電源(電池など)とは異なり、電圧\(V\)が一定ではないからです。コンデンサーの充電や放電では、時間経過と共に電位差\(V\)が変化します。例えば以下は、コンデンサーに対して充電するときのグラフです。
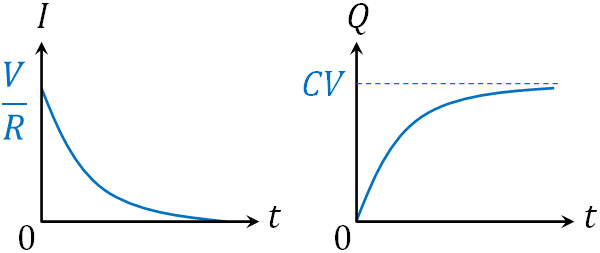
充電するとき、コンデンサーの抵抗は0です。ただ時間経過と共に抵抗が増えていきます。また、時間経過と共に電荷が蓄積することで電位差\(V\)が大きくなります。また放電では、逆の現象が起こります。
いずれにしても電圧(電位差)\(V\)が一定でないため、\(W=QV\)を利用してコンデンサーが行った仕事(コンデンサーがもつエネルギー)を計算することはできません。
コンデンサーの静電エネルギーは\(U=\displaystyle\frac{1}{2}QV\)
それでは、どのようにしてコンデンサーがもつエネルギー(コンデンサーが行う仕事)を計算すればいいのでしょうか。
仕事\(W\)を計算するとき、力\(F\)と移動距離\(x\)による面積を計算すればいいです。ただ電気の場合、\(W=Fx\)ではなく、仕事を得る公式は先ほど記した\(W=QV\)です。これはつまり、電圧\(V\)と電気量\(Q\)のグラフについて、面積を計算すれば仕事\(W\)を得られることを意味しています。
電圧\(V\)が一定の場合、\(W=QV\)によって仕事を計算できます。一方で電圧\(V\)と電気量\(Q\)が一定でない場合、グラフの面積を計算することによって仕事量(保有するエネルギー量)を計算するのです。
コンデンサーの公式より、\(Q=CV\)であるため、式を\(V=\displaystyle\frac{1}{C}×Q\)と変形できます。コンデンサーがもつ電気容量\(C\)は変化しないため、グラフの傾きが\(\displaystyle\frac{1}{C}\)である一次関数のグラフを作ることができます。
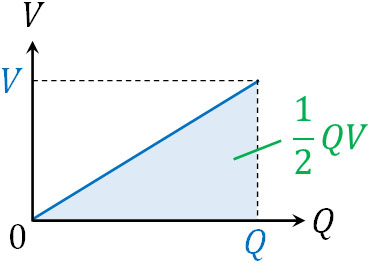
そこで、コンデンサーによる\(V-Q\)グラフの面積を計算しましょう。上図より、電気量が\(Q\)、電位差が\(V\)の場合、囲まれている部分の面積(コンデンサーが行う仕事\(W\))は以下のように計算できます。
- \(W=\displaystyle\frac{1}{2}QV\)
またコンデンサーが行う仕事というのは、コンデンサーがもともと保有していたエネルギーでもあります。仕事量と内部エネルギーは同じであることを力学で既に学んでいると思います。これは電気でも同じであり、仕事と内部エネルギーは意味が同じです。
コンデンサーでは、コンデンサーが保有しているエネルギーを静電エネルギーといいます。静電エネルギー\(U\)は先ほどの式を利用して、以下のように表すことができます。
- \(U=\displaystyle\frac{1}{2}QV\)
こうして、コンデンサーに蓄積されているエネルギーの公式を得ることができました。
多くの場合、教科書に静電エネルギーの公式が記載されており、公式を覚えることになります。ただ公式を覚えても意味がなく、なぜ\(U=\displaystyle\frac{1}{2}QV\)によってコンデンサーが保有するエネルギーを計算できるのか学びましょう。
静電エネルギーの公式を変形する
次に、静電エネルギーの公式を変形しましょう。コンデンサーの公式より、\(Q=CV\)です。そこで、\(Q=CV\)を\(U=\displaystyle\frac{1}{2}QV\)へ代入しましょう。そうすると、以下の公式を得られます。
- \(U=\displaystyle\frac{1}{2}CV^2\)
また\(Q=CV\)より、\(V=\displaystyle\frac{Q}{C}\)です。そこで、\(V=\displaystyle\frac{Q}{C}\)を\(U=\displaystyle\frac{1}{2}QV\)へ代入しましょう。そうすると、以下の公式を得られます。
- \(U=\displaystyle\frac{Q^2}{2C}\)
つまり、静電エネルギーを得る公式は3つあります。
- \(U=\displaystyle\frac{1}{2}QV=\displaystyle\frac{1}{2}CV^2=\displaystyle\frac{Q^2}{2C}\)
コンデンサーが保有するエネルギーは電気量\(Q\)、電圧\(V\)、電気容量\(C\)を利用することで計算できます。公式を暗記する必要はなく、公式を作れるようになりましょう。
静電エネルギーや電源がする仕事、ジュール熱の関係
次に静電エネルギーや電源がする仕事、ジュール熱の関係を確認しましょう。以下のように、直流回路で抵抗とコンデンサーが存在する回路を考えましょう。
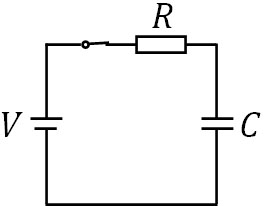
電源に接続することにより、コンデンサーに電荷が蓄積していきます。つまり、電源によって仕事が行われています。電源は電圧\(V\)が一定です。そのため、電荷\(Q\)を電圧\(V\)の高さまで持ち上げるとき、必要な仕事は先ほどの公式を利用して以下のように表すことができます。
- \(W=QV\)
つまり、電源による仕事量は\(W=QV\)です。それに対して、コンデンサーに蓄積する静電エネルギーは\(U=\displaystyle\frac{1}{2}QV\)です。
それでは、残りのエネルギー\(\displaystyle\frac{1}{2}QV\)はどこに消えたのでしょうか。答えをいうと、抵抗でジュール熱として熱エネルギーに変えられています。つまり、以下のようになっています。
- 電源による仕事 = 静電エネルギー + ジュール熱
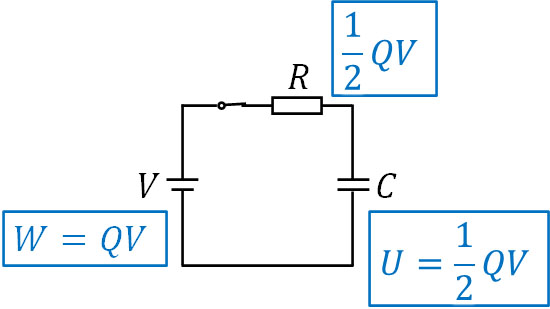
電源によって\(W=QV\)[J]の仕事が行われ、そのうち\(U=\displaystyle\frac{1}{2}QV\)[J]が静電エネルギーとしてコンデンサーに蓄積します。一方で残りの\(\displaystyle\frac{1}{2}QV\)[J]は抵抗でジュール熱となり、熱となって放出されるのです。
なお充電を開始して十分な時間が経過し、コンデンサーに電荷が蓄積した場合、コンデンサーに電流は流れなくなります。この場合、電流がないので\(\displaystyle\frac{1}{2}QV\)[J]以上のジュール熱の発生はありません。
参考までに、抵抗がない場合であっても電源による仕事は\(W=QV\)であり、コンデンサーに蓄積するエネルギーは\(U=\displaystyle\frac{1}{2}QV\)です。そのため、先ほどの計算と同様にジュール熱は\(\displaystyle\frac{1}{2}QV\)です。
この場合、導線による抵抗によって\(\displaystyle\frac{1}{2}QV\)[J]が熱エネルギーとして消費されたと考えます。
静電エネルギーとジュールの熱の計算に関する練習問題
それでは、コンデンサーの静電エネルギーと電源による仕事、ジュール熱に関する練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 以下のように、起電力\(V\)の電源にコンデンサー1(電気容量\(C\))、コンデンサー2(電気容量\(2C\))、コンデンサー3(電気容量\(C\))が導線でつながれています。すべてのコンデンサーは最初、電荷の蓄積がありません。
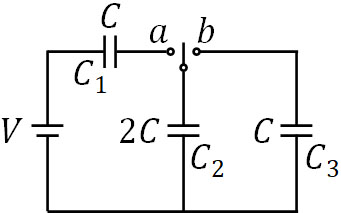
- スイッチを\(a\)につなぎ、十分な時間が経過した場合、回路で発生したジュール熱はいくらですか。
- その後、スイッチを\(b\)につなぎ、十分な時間が経過した場合、回路で発生したジュール熱はいくらですか。
- (1)と(2)を無限回繰り返す場合、回路で発生した全ジュール熱はいくらですか。
コンデンサーに電荷がない場合での仕事とジュール熱
1) スイッチを\(a\)につなぎ、十分な時間が経過した場合、回路で発生したジュール熱はいくらですか
コンデンサー1の電気量を\(Q_1\)、電圧を\(V_1\)とします。また、コンデンサー2の電気量を電気量\(Q_2\)、電圧を\(V_2\)とします。この場合、保存の法則より以下の式を作れます。
\(-Q_1+Q_2=0\)
\(Q_1=Q_2\)
\(CV_1=2CV_2\)
\(V_1=2V_2\) – ①
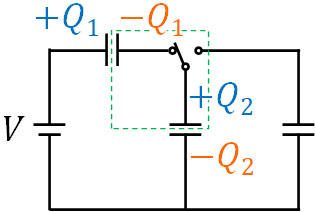
またキルヒホッフの第二法則より、以下の式を作りましょう。
\(V+(-V_1)+(-V_2)=0\) – ②
①と②より、以下のように計算できます。
\(V+(-V_1)+(-V_2)=0\)
\(V=V_1+V_2\)
\(V=2V_2+V_2\)
\(V_2=\displaystyle\frac{V}{3}\)
また\(V_2=\displaystyle\frac{V}{3}\)であるため、\(V_1=\displaystyle\frac{2V}{3}\)です。そのため、静電エネルギーはそれぞれ以下になります。
\(U_1=\displaystyle\frac{1}{2}C\left(\displaystyle\frac{2V}{3}\right)^2=\displaystyle\frac{2CV^2}{9}\)
\(U_2=\displaystyle\frac{1}{2}·2C\left(\displaystyle\frac{V}{3}\right)^2=\displaystyle\frac{CV^2}{9}\)
なお、仕事を計算できるようにするため、2つのコンデンサーを組み合わせた合成容量を計算しましょう。なお\(Q_1\)と\(Q_2\)の値は同じであるため、\(Q=Q_1=Q_2\)とします。
\(V=V_1+V_2\)
\(V=\displaystyle\frac{Q}{C}+\displaystyle\frac{Q}{2C}\)
\(V=\displaystyle\frac{3Q}{2C}\)
\(Q=\displaystyle\frac{2C}{3}V\)
こうして、2つのコンデンサーの合成容量は\(\displaystyle\frac{2C}{3}\)とわかりました。
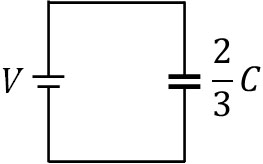
※合成容量を\(C’\)とするとき、\(\displaystyle\frac{1}{C’}=\displaystyle\frac{1}{C}+\displaystyle\frac{1}{2C}\)を利用して計算してもいいです。
\(Q=CV\)が公式なので、合成容量を公式に当てはめると\(Q=\displaystyle\frac{2CV}{3}\)です。つまり、2つのコンデンサーに対して電源が行った仕事は以下のように計算できます。
\(W=QV\)
\(W=\displaystyle\frac{2CV}{3}×V\)
\(W=\displaystyle\frac{2CV^2}{3}\)
そのため、以下の式によって回路で発生したジュール熱を計算できます。
\(\displaystyle\frac{2CV^2}{3}-\left(\displaystyle\frac{2CV^2}{9}+\displaystyle\frac{CV^2}{9}\right)\)
\(=\displaystyle\frac{2CV^2}{3}-\displaystyle\frac{CV^2}{3}\)
\(=\displaystyle\frac{CV^2}{3}\)
こうして、発生したジュール熱は\(\displaystyle\frac{CV^2}{3}\)とわかります。
電荷をもつコンデンサーによるエネルギーの変化
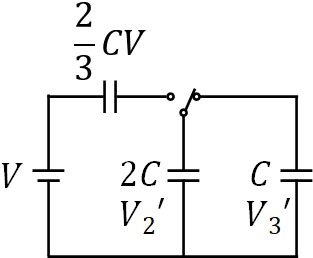
2) その後、スイッチを\(b\)につなぎ、十分な時間が経過した場合、回路で発生したジュール熱はいくらですか
先ほどの計算より、\(Q_1=Q_2=\displaystyle\frac{2CV}{3}\)です。ただスイッチを\(b\)につなぐことにより、コンデンサー1は切断されるため、コンデンサー2とコンデンサー3のみを考えましょう。
なお、(2)の操作によってそれぞれのコンデンサーの電位差が\(V_2’\)と\(V_3’\)の場合、キルヒホッフの第二法則より、以下のようになります。
\(V_2’=V_3’\) – ③
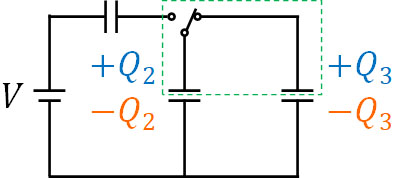
また電気量保存の法則より、回路の独立部分に着目すると、以下の式を作れます。
\(\displaystyle\frac{2CV}{3}=Q_2+Q_3\)
\(\displaystyle\frac{2CV}{3}=2CV_2’+CV_3’\)
\(\displaystyle\frac{2V}{3}=2V_2’+V_3’\) – ④
③と④より、以下のように計算しましょう。
\(\displaystyle\frac{2V}{3}=2V_2’+V_3’\)
\(\displaystyle\frac{2V}{3}=2V_2’+V_2’\)
\(V_2’=\displaystyle\frac{2V}{9}\)
また\(V_2’=\displaystyle\frac{2V}{9}\)であるため、\(V_3’=\displaystyle\frac{2V}{9}\)です。そのため、それぞれのコンデンサーの静電エネルギーは以下のようになります。
\(U_2’=\displaystyle\frac{1}{2}·2C\left(\displaystyle\frac{2V}{9}\right)^2=\displaystyle\frac{4CV^2}{81}\)
\(U_3’=\displaystyle\frac{1}{2}C\left(\displaystyle\frac{2V}{9}\right)^2=\displaystyle\frac{2CV^2}{81}\)
なお、電源による仕事は0です。そのため変化前から変化後を引くと、消費されたジュール熱を計算できます。
- 変化前の静電エネルギー = 変化後の静電エネルギー + 消費されたジュール熱
そこで、以下のように計算しましょう。
\(\displaystyle\frac{CV^2}{9}-\left(\displaystyle\frac{4CV^2}{81}+\displaystyle\frac{2CV^2}{81}\right)\)
\(=\displaystyle\frac{9CV^2}{81}-\displaystyle\frac{6CV^2}{81}\)
\(=\displaystyle\frac{CV^2}{27}\)
こうして、発生したジュール熱は\(\displaystyle\frac{CV^2}{27}\)とわかります。
電流が流れないコンデンサーでの静電エネルギーと仕事、ジュール熱
3) (1)と(2)を無限回繰り返す場合、回路で発生した全ジュール熱はいくらですか。
(1)と(2)の操作を何度も繰り返す場合、どこかの段階ですべてのコンデンサーは充電が完了し、電流が流れなくなります。つまり、以下のように導線をつないで十分な時間が経過した後の状態を考えればいいです。
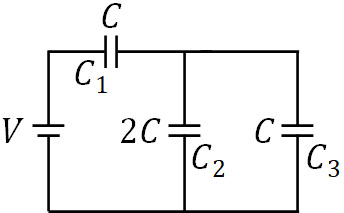
そこで、コンデンサーの電荷がない状態で電源に接続する場合について、それぞれのコンデンサーの静電エネルギーを求め、発生するジュール熱を計算しましょう。
電気量保存の法則より、式を作りましょう。なお、それぞれの電位差を\(V_1\)、\(V_2\)、\(V_3\)とします。
\(-Q_1+Q_2+Q_3=0\)
\(-CV_1+2CV_2+CV_3=0\) – ⑤

またキルヒホッフの法則より、以下の式を作ることができます。
\(V+(-V_1)+(-V_2)=0\)
\(V=V_1+V_2\) – ⑥
同様にキルヒホッフの法則より、以下の式を作ることができます。
\(V_2+(-V_3)=0\)
\(V_2=V_3\) – ⑦
⑤と⑥と⑦より、以下のように計算できます。
\(-CV_1+2CV_2+CV_3=0\)
\(CV_1=3CV_2\)
\(V_1=3V_2\)
\(V-V_2=3V_2\)
\(V_2=\displaystyle\frac{1}{4}V\)
\(V_2=\displaystyle\frac{1}{4}V\)なので、\(V_1=\displaystyle\frac{3}{4}V\)です。また、\(V_3=\displaystyle\frac{1}{4}V\)です。
そこで、それぞれのコンデンサーの静電エネルギーを計算しましょう。
\(U_1=\displaystyle\frac{1}{2}C\left(\displaystyle\frac{3V}{4}\right)^2=\displaystyle\frac{9CV^2}{32}\)
\(U_2=\displaystyle\frac{1}{2}·2C\left(\displaystyle\frac{V}{4}\right)^2=\displaystyle\frac{CV^2}{16}\)
\(U_3=\displaystyle\frac{1}{2}C\left(\displaystyle\frac{V}{4}\right)^2=\displaystyle\frac{CV^2}{32}\)
それでは、電源がした仕事はいくらでしょうか。コンデンサー2とコンデンサー3は並列接続であるため、合成容量は\(2C+C=3C\)です。次に、すべてのコンデンサーの合成容量\(C’\)を計算しましょう。
\(\displaystyle\frac{1}{C’}=\displaystyle\frac{1}{C}+\displaystyle\frac{1}{3C}\)
\(\displaystyle\frac{1}{C’}=\displaystyle\frac{4}{3C}\)
\(C’=\displaystyle\frac{3}{4}C\)
こうして、合成容量は\(\displaystyle\frac{3}{4}C\)とわかります。つまり、コンデンサーを一つに集約すると以下の回路になります。
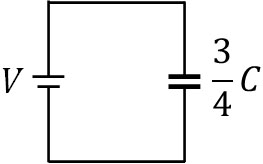
そのため、電源による仕事を以下のように計算できます。
\(W=QV\)
\(W=\displaystyle\frac{3}{4}CV×V\)
\(W=\displaystyle\frac{3CV^2}{4}\)
そこで、電源による仕事から静電エネルギーを引きましょう。
\(\displaystyle\frac{3CV^2}{4}-\left(\displaystyle\frac{9CV^2}{32}+\displaystyle\frac{CV^2}{16}+\displaystyle\frac{CV^2}{32}\right)\)
\(=\displaystyle\frac{3CV^2}{8}\)
こうして、発生したジュール熱は\(\displaystyle\frac{3CV^2}{8}\)と計算できました。
コンデンサーがもつエネルギーと電源による仕事、ジュール熱を計算する
電荷をもつコンデンサーはエネルギーをもっています。電気を学ぶとき、どれだけのエネルギーをもっているのか計算できるのは重要です。そこで、静電エネルギーを計算する公式の意味を学び、公式を利用できるようになりましょう。
なおエネルギーと仕事は意味が同じです。仕事を行う場合、それに伴ってエネルギーが増えます。ただコンデンサーにエネルギーを与えるとき、すべて静電エネルギーとして蓄積することはなく、一部は熱エネルギーとして放出されます。
そこで、これまで学んだ知識を利用して発生したジュール熱を計算できるようになりましょう。コンデンサーに関するさまざまな知識を利用することにより、電源による仕事とジュール熱の計算が可能です。
コンデンサーの静電エネルギーに加えて、電源による仕事やジュール熱の計算をする場合、計算方法が複雑になります。そこで、公式の意味と計算過程を理解して問題を解けるようになりましょう。