交流電源を利用するとき、時間経過によって電圧が変化します。このとき電圧が変化することにより、交流回路の電流がどのように変化するのか学びましょう。
回路でひんぱんに利用される部品が抵抗・コンデンサー・コイルです。それぞれ特徴が異なり、電圧と電流の関係を理解しなければいけません。電圧が高くても、電流がゼロであることがひんぱんにあるからです。つまり、位相のずれを生じます。
また、コンデンサーやコイルはそれ自体を抵抗とみなすことができます。つまり、オームの法則を利用できます。
それでは交流回路に抵抗・コンデンサー・コイルがあるとき、電流の値やグラフ、消費電力をどのように計算すればいいのでしょうか。そこで、これらの部品が回路に一つ存在する場合、交流回路で起こる現象を解説していきます。
もくじ
電圧と電流には位相のずれがある
直流回路では、電圧が大きければ電流の値も大きいです。オームの法則より、\(V=RI\)です。これが、電圧が大きいと電流も大きくなる理由です。
一方、交流回路ではこの考え方が当てはまりません。つまり電圧が高くても、電流が大きいとは限らないのです。むしろ、電圧がゼロのときに電流が最大になることもあります。つまり、以下の関係は成り立ちません。
- 電圧が\(V=V_0sinωt\)の場合、電流は\(I=I_0sinωt\)
なぜ、この関係が成り立たないのでしょうか。この理由を理解しなければいけません。
電圧と電流の最大値が異なるため、交流回路では位相にずれを生じます。位相というのは、角度を表します。例えば\(θ=0\)のとき、\(sinθ\)と\(sinθ+\displaystyle\frac{π}{2}\)では値が異なります。これは、位相がずれているからです。
交流回路では、このような位相のずれを生じています。そこで電圧\(V\)に対して、どれだけ電流の位相がずれているのか確認しましょう。
交流と抵抗:位相のずれはなく、同位相となる
まず、交流回路に一つの抵抗がつながっている場面を考えましょう。以下のような回路で起こる現象を学ぶのです。

抵抗というのは、電圧が大きい場合、電流も大きくなります。そのため位相のずれを考える必要はなく、同位相になります。このとき、以下のように電圧\(V\)が変化するとします。
- \(V=V_0sinωt\)
オームの法則\(V=RI\)より、\(I=\displaystyle\frac{V}{R}\)であるため、式は以下のようになります。
- \(I=\displaystyle\frac{V_0sinωt}{R}\)
なお\(\displaystyle\frac{V_0}{R}=I_0\)とすると、\(V_0\)は電圧の最大値であるため、\(I_0\)は電流の最大値となります。つまり、以下の式となります。
- \(I=I_0sinωt\)
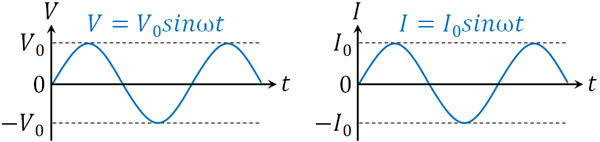
こうして、抵抗が交流回路に存在する場合は同位相になるとわかりました。抵抗というのは、電圧と電流の位相が同じになると理解しましょう。
消費電力は\(\overline{P}=I_eV_e\)となる
抵抗が交流回路に存在する場合、電圧と電流が同位相であるため、電力の計算が可能です。電力\(P\)を得る公式は以下になります。
- \(P=IV\)
電圧の最大値が\(V_0\)、電流の最大値が\(I_0\)であるため、電力の最大値は\(P=I_0V_0\)です。このとき、平均値\(\overline{P}\)を求めましょう。
交流は円運動の公式と同じであるため、山と谷の面積が等しいです。そのため、平均値\(\overline{P}\)は以下のようになります。
- \(\overline{P}=\displaystyle\frac{1}{2}I_0V_0\)
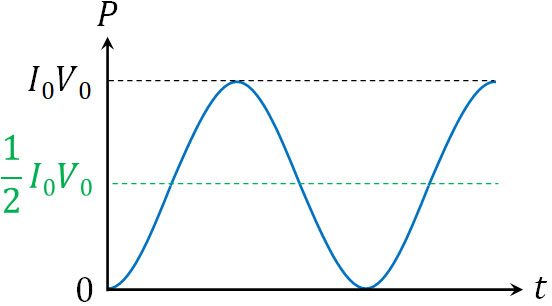
なお、電圧と電流でそれぞれ\(\displaystyle\frac{1}{2}\)を分担すると以下のように式を変形できます。
- \(\overline{P}=\displaystyle\frac{1}{\sqrt{2}}I_0×\displaystyle\frac{1}{\sqrt{2}}V_0\)
そこで実効値を利用し、\(I_e=\displaystyle\frac{1}{\sqrt{2}}I_0\)と\(V_e=\displaystyle\frac{1}{\sqrt{2}}V_0\)を代入すると以下のようになります。
- \(\overline{P}=I_eV_e\)
こうして、交流回路に抵抗が存在する場合の平均消費電力\(\overline{P}\)を計算できます。電圧と電流での位相のずれがないため、交流と抵抗の関係は理解しやすいです。
コンデンサーと交流:電流の位相は電圧より\(\displaystyle\frac{π}{2}\)進む
それに対して、交流回路にコンデンサーが一つ存在する場合はどのように考えればいいのでしょうか。
コンデンサーには電荷を蓄える性質があります。直流回路では、スイッチを入れた直後はコンデンサーの抵抗がゼロであるため、電流の大きさは最大になります。言い換えると、コンデンサーの電荷がゼロのとき、電流の大きさが最大になります。
コンデンサーの電荷がゼロになる場面というのは、交流電源で電圧の向きが変わるときです。つまり\(V=0\)のとき、コンデンサーの電荷がゼロになり、電流の値は最大になります。
一方で電圧が増加すると、それに伴ってコンデンサーには電荷が蓄えられるようになります。このとき、電圧の最大値が\(V_0\)であり、コンデンサーを含む以下の交流回路があるとします。
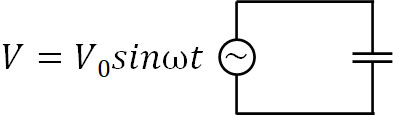
この回路について、以下のようにイメージしましょう。
- スイッチを入れた瞬間(電源の電圧:\(V=0\))では、コンデンサーの抵抗はゼロなので電流が最大となる(\(I=I_0\))。
- 電圧が最大のとき(\(V=V_0\))、コンデンサーに電荷が十分に溜まっているため、自由電子の移動がなく電流はゼロになる。また、コンデンサーの電位差は最大となる。
- 電圧は高さであるため、電源の電圧が下がると、それに伴ってコンデンサーの電圧(電位差)も下落する。このとき、自由電子はそれまでとは反対側に移動を開始し、\(V=0\)となったときに電流が最大となる。
- 時間が経つと、先ほどとは反対側に電荷が溜まり、電圧が最大になると同時に再び電流がゼロになる。
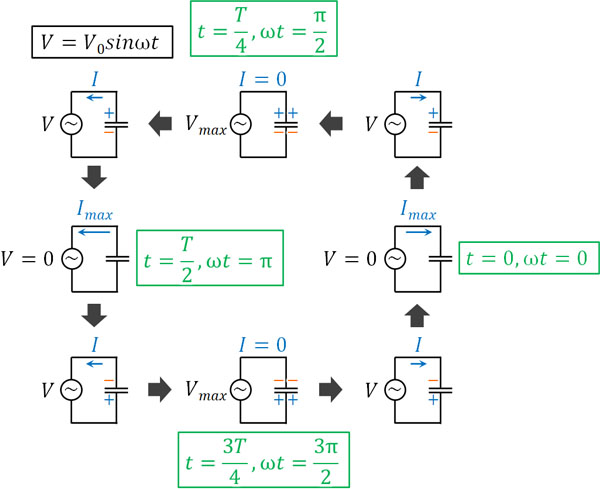
つまり、以下のようになります。
- 電圧がゼロ:電流は最大
- 電圧が最大:電流はゼロ
電圧がゼロのとき、コンデンサーの抵抗もゼロであるため、前述の通り電流が最大となります。言い換えると、電流の位相は電圧よりも\(\displaystyle\frac{π}{2}\)進んでいることになります。そのため電圧の式が\(V=V_0sinωt\)のとき、電流の式は以下になります。
- \(I=I_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
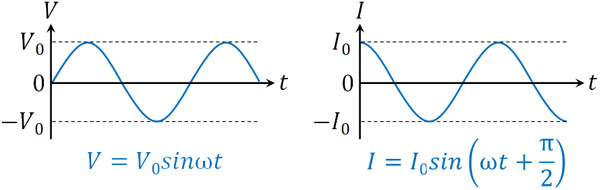
なお、\(I=I_0cosωt\)と表してもいいです。グラフを確認すると、\(t=0\)のときに最大値となる必要があり、\(cos0°=1\)であるため\(I=I_0cosωt\)が成り立ちます。いずれにしても、sinを利用して式をそろえると、位相が\(\displaystyle\frac{π}{2}\)ずれているとわかります。
微分を利用し、電流の位相の公式を得る
参考までに、コンデンサーによる位相のずれが\(I=I_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)となるのは、微分を利用することによって証明できます。微分を利用するため、難しい場合は読み飛ばし、「コンデンサーの位相は\(\displaystyle\frac{π}{2}\)のずれを生じる」と暗記しても問題ありません。
キルヒホッフの法則より、電源とコンデンサーの電圧は同じです。そのため、電源の電圧とコンデンサーの電圧は両方とも\(V=V_0sinωt\)です。
また、電流の定義は単位時間当たり(1秒あたり)の電気量を指します。そのため、\(I=\displaystyle\frac{ΔQ}{Δt}\)です。また電気量の公式より、\(Q=CV\)であるため、以下のように式を変形できます。
\(I=\displaystyle\frac{ΔQ}{Δt}\)
\(I=\displaystyle\frac{CΔV}{Δt}\)
\(I=\displaystyle\frac{CV_0Δsinωt}{Δt}\)
\(I=CV_0\displaystyle\frac{Δsinωt}{Δt}\)
電気容量\(C\)と電圧の最高値\(V_0\)は定数です。そこで、\(\displaystyle\frac{Δsinωt}{Δt}\)に着目しましょう。
なお\(\displaystyle\frac{Δsinωt}{Δt}\)というのは、\(t\)が変化するときの値(傾き)の計算を意味します。言い換えると、\(t\)の微分を意味します。そこで、\(I=CV_0\displaystyle\frac{Δsinωt}{Δt}\)を微分しましょう。
- \(I=CV_0ω·cosωt\)
こうして、\(I=CV_0ω·cosωt\)とわかりました。また\(I_0=ωCV_0\)とすると、以下のように変形できます。
- \(I=I_0cosωt\)
これが、交流回路にコンデンサーが含まれる場合の電流の公式です。なお\(cosθ=sin\left(θ+\displaystyle\frac{π}{2}\right)\)であるため、以下のように式を変えることができます。
- \(I=I_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
微分を利用することにより、「電流では電圧よりも位相が\(\displaystyle\frac{π}{2}\)進んでいる」と正確にわかります。
コンデンサーを抵抗とみなせる:容量性リアクタンスの公式
先ほど、計算過程で\(I_0=ωCV_0\)であるとわかりました。\(I_0=ωCV_0\)を変形すると\(V_0=\displaystyle\frac{1}{ωC}I_0\)になります。このときオームの法則は\(V=RI\)であるため、\(R=\displaystyle\frac{1}{ωC}\)であれば、オームの法則を満たすとわかります。
コンデンサーは抵抗としても機能します。コンデンサーに電荷が蓄積すると電流を通さなくなるため、コンデンサーは抵抗でもあるのです。先ほどの結果より、コンデンサーの抵抗は\(R=\displaystyle\frac{1}{ωC}\)が該当します。このとき、\(\displaystyle\frac{1}{ωC}\)をコンデンサーの容量性リアクタンスといいます。
コンデンサーの抵抗が\(R=\displaystyle\frac{1}{ωC}\)であるとわかると、オームの法則を利用して、以下のように式を作ることができます。
- \(V=\displaystyle\frac{1}{ωC}I\)
※\(ω\):角周波数、\(C\):電気容量
交流回路にコンデンサーが存在する場合、\(R=\displaystyle\frac{1}{ωC}\)を利用してコンデンサーの抵抗を計算し、オームの法則を利用しましょう。
なお、\(V=\displaystyle\frac{1}{ωC}I\)は実効値を利用する場合であっても成り立ちます。実効値を利用したい場合、電圧の最大値\(V_0\)と電流の最大値\(I_0\)を\(\sqrt{2}\)で割りましょう。また\(V_e=\displaystyle\frac{1}{\sqrt{2}}V_0\)、\(I_e=\displaystyle\frac{1}{\sqrt{2}}I_0\)とすると以下の式になります。
- \(V_e=\displaystyle\frac{1}{ωC}I_e\)
電圧と電流について、最大値になるタイミングは異なります。ただ交流回路を直流回路とみなして平均値を計算すると、先ほどの式が成り立つのです。
コンデンサーが存在する場合の消費電力
次に、コンデンサーが存在する場合での消費電力を計算しましょう。先ほど解説した通り、\(I=I_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)を\(I=I_0cosωt\)と変形できます。また、電力を得る公式は\(P=IV\)です。そこで、以下のように計算しましょう。
\(P=I_0cosωt·V_0sinωt\)
\(P=\displaystyle\frac{I_0V_0}{2}sin2ωt\)
2倍角の公式より、\(sin2θ=2sinθcosθ\)です。そのため、このように計算できます。そこで、\(P=\displaystyle\frac{I_0V_0}{2}sin2ωt\)のグラフを描きましょう。
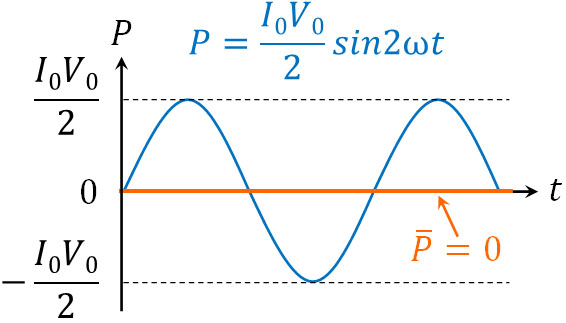
グラフを確認すると、消費電力の平均値は\(\overline{P}=0\)であるとわかります。つまり抵抗とは異なり、コンデンサーでは電力の消費がありません。言い換えると、ジュール熱の発生はありません。
なぜ、電力の消費がないのでしょうか。コンデンサーは電荷を蓄積する性質があります。電源により、コンデンサーへ電荷が送られるのです。ただ電源の電圧が下がると、電荷が逆流することによって、コンデンサーから電源へ電荷が送られます。そのため、消費電力の平均はゼロになるのです。
なお、消費電力が常にゼロという意味ではなく、平均がゼロになります。交流では周期的に同じ現象が繰り返されるため、平均を利用することによって回路で何が起こっているのか理解しましょう。
コイルが交流回路にある場合の現象
それでは、交流回路にコイルが一つ存在する場合はどのような現象が起こるのでしょうか。以下の回路を考えてみましょう。
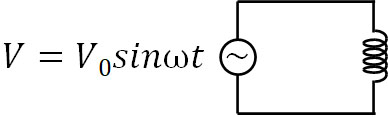
コイルは磁場の変化を嫌います。そのため電源にスイッチを入れても電流はゼロです。電圧が発生しても、コイルによる電磁誘導(自己誘導)によって電流を打ち消し合い、電流は流れません。ただ時間が経過するとコイルは磁場の変化に慣れ、電流を通すようになります。
つまり電圧が変化した後、コイルでは電流が流れるまでに時間がかかります。そのため電圧が最大値に達した後、コイルを流れる電流が最大値に達します。コンデンサーと同様に、コイルを利用する場合も位相のずれがあるのです。
具体的には、コイルを利用する場合、周期を\(T\)をとすると\(\displaystyle\frac{T}{4}\)の位相のずれを生じます。イメージとしては、以下のようになります。
- 電圧は最大になるものの、自己誘導によってコイルを流れる電流はゼロ。
- 電圧が下がるにつれて電流は大きくなり、電圧がゼロになると電流は最大値となる。
- 先ほどとは逆の電圧になると、自己誘導によって再び電流が小さくなる
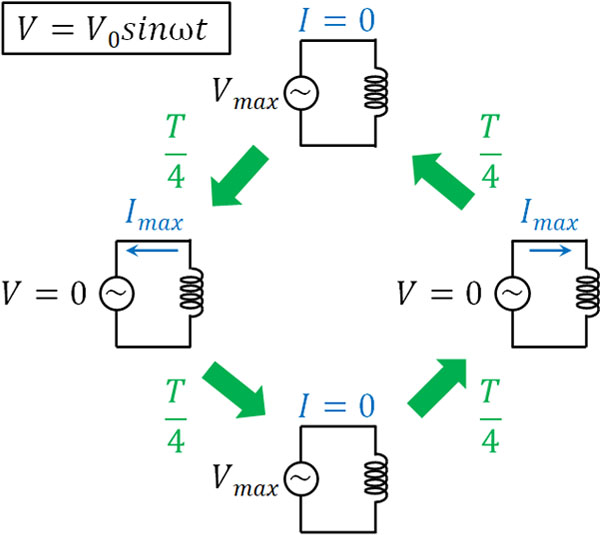
なお、電圧に対して電流が\(\displaystyle\frac{T}{4}\)遅れるというのは、電圧に対して電流は位相が\(\displaystyle\frac{π}{2}\)遅れることを意味しています。\(\displaystyle\frac{T}{4}\)を位相で表すと\(\displaystyle\frac{π}{2}\)だからです。
そのため交流回路にコイルが一つ存在する場合、コイルを流れる電流を以下のように表すことができます。
- \(I=I_0sin\left(ωt-\displaystyle\frac{π}{2}\right)\)
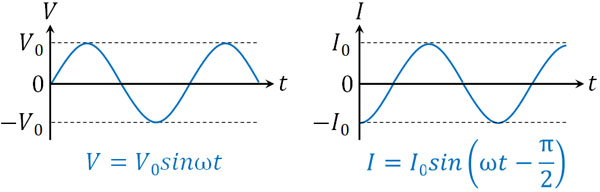
位相が遅れているため、\(\displaystyle\frac{π}{2}\)を引くことによって電流を表す公式を作ることができます。また、この式を\(I=-I_0cosωt\)と記すこともできます。
積分を利用して公式を得る
なお、先ほどの公式を導き出すときは積分を利用します。そのためより詳しく知りたい場合、積分を利用することによって、先ほどの式を導出する方法を学びましょう。難しい場合、この部分は読み飛ばして、位相が\(\displaystyle\frac{π}{2}\)遅れることを暗記しても問題ありません。
キルヒホッフの法則より、電源とコイルの電圧は同じです。そのため、電源の電圧とコイルの電圧は両方とも\(V=V_0sinωt\)です。
また、自己誘導によってコイルに生じる電圧は\(V=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)です。そのため、以下のように計算できます。
\(V=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)
\(V_0sinωt=L\displaystyle\frac{ΔI}{Δt}\)
\(\displaystyle\frac{ΔI}{Δt}=\displaystyle\frac{V_0sinωt}{L}\)
\(\displaystyle\frac{ΔI}{Δt}\)というのは、「電流\(I\)を時間\(t\)で微分する」という意味です。そのため両辺を\(t\)で積分すれば、微分前の状態(電流\(I\))を得ることができます。微分によって\(\displaystyle\frac{V_0sinωt}{L}\)となるのであれば、元に戻すために積分しましょう。以下のようになります。
\(I=\displaystyle \int \displaystyle\frac{V_0sinωt}{L} dt\)
\(I=\displaystyle\frac{V_0}{L}\displaystyle \int sinωt dt\)
\(I=\displaystyle\frac{V_0}{L}\left(-\displaystyle\frac{1}{ω}cosωt\right)\)
\(I=-\displaystyle\frac{V_0}{ωL}cosωt\)
こうして、\(I=-\displaystyle\frac{V_0}{ωL}cosωt\)であるとわかりました。また\(I_0=\displaystyle\frac{V_0}{ωL}\)とすると、式は以下のようになります。
- \(I=-I_0cosωt\)
なお\(-cosθ=sin\left(θ-\displaystyle\frac{π}{2}\right)\)なので、以下のように式を変形しましょう。
- \(I=I_0sin\left(ωt-\displaystyle\frac{π}{2}\right)\)
こうして、交流回路にコイルがある場合は位相が\(\displaystyle\frac{π}{2}\)遅れると証明できました。
抵抗として誘導性リアクタンスを得る
次に、交流回路にコイルがあるときの抵抗を計算しましょう。\(I_0=\displaystyle\frac{V_0}{ωL}\)を変形すると、\(V_0=ωL·I_0\)となります。オームの法則\(V=RI\)と比べると、コイルの抵抗\(R\)は\(ωL\)が該当するとわかります。
\(ωL\)は誘導性リアクタンスと呼ばれ、誘導性リアクタンスはコイルの抵抗と認識しましょう。そのため、オームの法則を利用して以下の関係が成り立ちます。
- \(V=ωL·I\)
また実効値を利用すると、以下の関係も成り立ちます。
- \(V_e=ωL·I_e\)
コイルが交流回路に存在する場合、コイルの抵抗として\(R=ωL\)を利用しましょう。
交流回路では、コイルの消費電力はゼロ
それでは、コイルの消費電力はどのようになるのでしょうか。先ほどと同様に、電力\(P\)の計算をしましょう。なお、電流の式は\(I=-I_0cosωt\)を使います。
\(P=IV\)
\(P=-I_0cosωt·V_0sinωt\)
\(P=-\displaystyle\frac{I_0V_0}{2}sin2ωt\)
グラフにすると、以下のようになります。
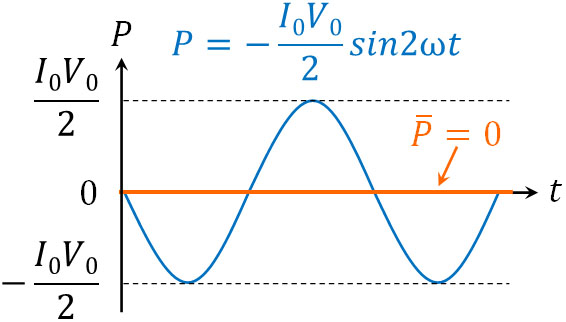
グラフを確認すると、電力の平均\(\overline{P}\)はゼロであるとわかります。コンデンサーと同様に、交流回路にコイルが存在する場合も消費電力の平均はゼロとなるのです。
交流回路に抵抗・コンデンサー・コイルがあるときの考え方
交流を学ぶとき、ここまでの内容を整理して覚える必要があります。表にすると、以下のようになります。
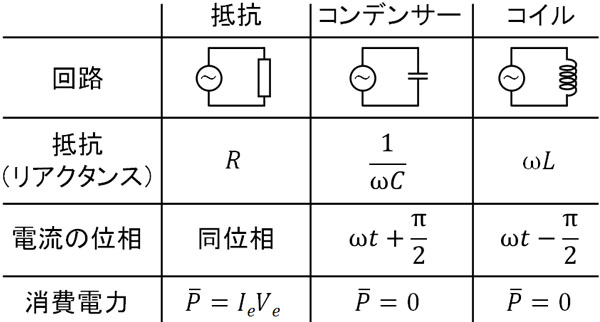
このように整理することで、回路に抵抗やコンデンサー、コイルが含まれるとき、どのような現象が起こるのか確認しましょう。
抵抗については、同位相なので考え方は簡単です。一方、回路にコンデンサーとコイルが存在する場合、位相がずれます。両方とも\(\displaystyle\frac{π}{2}\)のずれがあり、電圧に対して電流の位相が早くなるのか、それとも遅くなるのか見分けましょう。
抵抗、コンデンサー、コイルが回路に存在するケースは多く、交流回路でどのような現象が起こるのか理解する必要があります。