コンデンサーに対して、極板間へ導体(金属)を挿入するケースがあります。この場合、極板間の距離が短くなります。その結果、電位差が変化します。
極板間の距離に変化があるというのは、コンデンサーの電気容量が変わることを意味します。これが電位差に影響するのです。一方、コンデンサーに蓄積している電気量や2枚の金属板による電場に変化はありません。
なぜ、これらの変化が起こるのか理解しましょう。結果を覚えても意味がなく、物理現象が起こる原理を学ぶ必要があります。
それでは、導体の挿入によって極板間の距離が変化するとき、どのように計算すればいいのでしょうか。コンデンサーの間に金属を入れるときの変化を解説していきます。
もくじ
導体の厚さの分だけ極板間の距離が短くなる
電気量\(Q\)をもつコンデンサーに対して、厚さ\(t\)の導体(金属板)を挿入する場面を考えましょう。結論をいうと、この場合は導体の厚さの分だけ極板間の距離が短くなります。
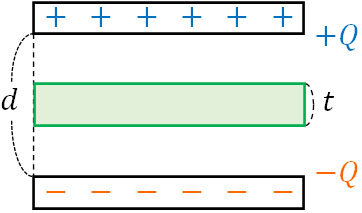
例えばコンデンサーの極板間の距離が5mmであり、厚さ1mmの金属板をコンデンサーの間に挿入する場合、そのコンデンサーの極板間の距離は4mmとみなすことができます。
これにより、電気容量が増えます。復習すると、コンデンサーの電気容量\(C\)を得る公式は以下になります。
- \(C=ε\displaystyle\frac{S}{d}\)
\(S\)は面積、\(d\)は極板間の距離、\(ε\)は比例定数(誘電率)です。この公式を確認すればわかる通り、極板間の距離が短くなる場合、コンデンサーの電気容量は大きくなるのです。
導体を導線とみなし、コンデンサーの電気容量を計算する
それでは、導体をコンデンサーの極板内に挿入することにより、なぜ厚さの分だけ極板間の距離が短くなるとみなせるのでしょうか。
電場内に導体があると、静電誘導により、以下のように導体(金属)の表面に電荷が表れます。
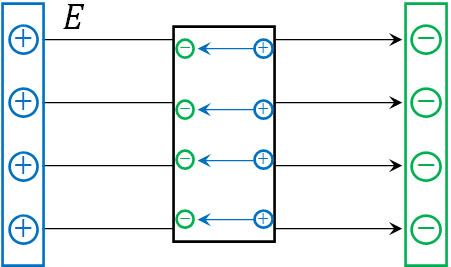
その結果、外部の電場と反対向き&同じ大きさにて、導体内に新たな電場が発生します。これにより、互いの電場が打ち消し合うことによって、導体内の電場はゼロになります。
導体は電気を通すため、役割は導線と同じです。そこで、導体を導線とみなしましょう。つまり、極板内に導体を挿入することにより、2つのコンデンサーが直列接続している状態と同じになります。
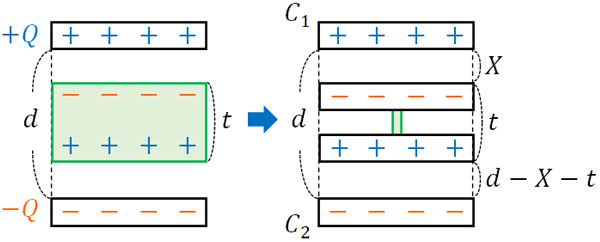
それでは上の右図を利用して、導体を挿入した後のコンデンサーの電気容量\(C’\)を計算しましょう。金属板の面積を\(S\)、誘電率を\(ε\)とすると、コンデンサーの公式より電気容量\(C_1\)は以下のように表すことができます。
\(C_1=ε\displaystyle\frac{S}{X}\)
また、電気容量\(C_2\)は以下のように表すことができます。
\(C_2=ε\displaystyle\frac{S}{d-X-t}\)
次に、導体を挿入した後の電気容量を計算しましょう。つまり、\(C_1\)と\(C_2\)の合成容量を計算します。
\(\displaystyle\frac{1}{C’}=\displaystyle\frac{1}{C_1}+\displaystyle\frac{1}{C_2}\)
\(\displaystyle\frac{1}{C’}=\displaystyle\frac{X}{εS}+\displaystyle\frac{d-X-t}{εS}\)
\(\displaystyle\frac{1}{C’}=\displaystyle\frac{d-t}{εS}\)
\(C’=ε\displaystyle\frac{S}{d-t}\)
こうして、合成容量は\(C’=ε\displaystyle\frac{S}{d-t}\)と計算できました。
導体を挿入前の電気容量は\(C=ε\displaystyle\frac{S}{d}\)です。一方、導体を挿入することにより、コンデンサーの電気容量は\(C’=ε\displaystyle\frac{S}{d\color{red}{-t}}\)となります。式を確認すると、極板の距離\(d\)から導体の厚さ\(t\)を引くことにより、導体挿入後のコンデンサーの電気容量を得られるとわかります。
導体をコンデンサーの中に入れるというのは、導体の厚みの分だけ、コンデンサーの極板の距離が短くなっていると認識しましょう。
電気量や電場は変化せず、極板間の電位差と距離が変化する
それでは、極板内に導体を入れることによって、何が変化し、何が変化しないのでしょうか。以下の要素について確認しましょう。
- 電気容量\(C\):大きくなる
- 電位差\(V\):減少する
- 電気量\(Q\):変化なし
- 電場\(E\):変化なし
結論と共に記しましたが、このような変化があります。電気容量\(C\)が大きくなる理由は先ほど解説しました。
また電位差の公式は\(V=Ed\)であり、導体を挿入することによって\(d\)が\(d-t\)に変わります。そのため、導入を挿入することによって電位差が小さくなります。
それに対して、電気量\(Q\)は変化しません。電気を学ぶとき、電気が勝手に生まれたり消えたりしないことは既に学んでいると思います。電気量保存の法則により、電気量\(Q\)に変化はないのです。また電気量\(Q\)に変化がない以上、電場\(E\)の変化もありません。
挿入する金属が短い場合の計算方法
それでは導体(金属)を挿入するとき、コンデンサーの極板と同じ大きさの金属板を挿入するのではなく、長さの短い金属板を挿入する場合はどのように計算すればいいのでしょうか。練習問題と共に考え方を学んでいきましょう。
以下の問題の答えは何でしょうか。
- 「一辺の長さが\(2L\)である正方形の極板」を有するコンデンサーがあり、極板間の距離は\(2d\)です。なお、極板間の誘電率を\(ε\)とします。このコンデンサーにたて\(2L\)、横\(L\)、高さ\(d\)の金属板を挿入する場合、電気容量はどのように変化しますか。
電気容量の変化を計算するため、まず元の状態での電気容量を求めましょう。一辺の長さは\(2L\)なので、極板の面積は\(4L^2\)です。そのため、電気容量\(C\)は以下のようになります。
\(C=ε\displaystyle\frac{4L^2}{2d}\)
\(C=ε\displaystyle\frac{2L^2}{d}\)
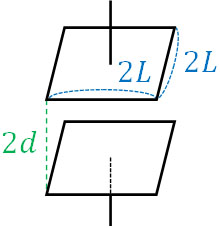
それでは、金属板(導体)を挿入する場合はどのようになるのでしょうか。下図のようになります。
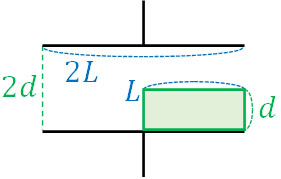
導体がコンデンサー内に存在するのかどうかによって電気容量が変化します。そこで以下のように、電気容量の異なるコンデンサーが2つ並列接続で存在していると考えて計算しましょう。
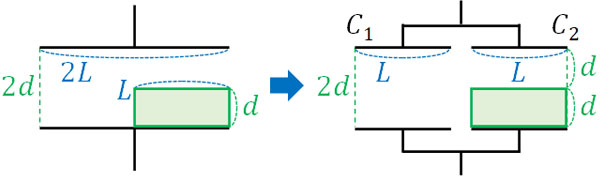
そこで、一方のコンデンサーの電気容量を\(C_1\)、もう一方のコンデンサーの電気容量を\(C_2\)として、合成容量\(C’\)を計算しましょう。なお、それぞれのコンデンサーの面積は\(L×2L=2L^2\)になります。そのため、電気容量は以下のようになります。
- \(C_1=ε\displaystyle\frac{2L^2}{2d}=ε\displaystyle\frac{L^2}{d}\)
- \(C_2=ε\displaystyle\frac{2L^2}{d}\)
また2つのコンデンサーは並列接続であるため、2つの電気容量を足すことで合成容量を計算しましょう。
\(C’=ε\displaystyle\frac{L^2}{d}+ε\displaystyle\frac{2L^2}{d}\)
\(C’=ε\displaystyle\frac{3L^2}{d}\)
こうして、\(C’=ε\displaystyle\frac{3L^2}{d}\)とわかりました。導体を挿入する前の電気容量は\(C=ε\displaystyle\frac{2L^2}{d}\)であるため、導体を挿入することによって電気容量(合成容量)は1.5倍になっています。そのため、電気容量が1.5倍になるのが答えです。
挿入前後の静電エネルギーの変化
次に、金属をコンデンサー内に挿入することによって、静電エネルギーがどのように変化するのか確認しましょう。挿入前と挿入後の静電エネルギーを計算することにより、どのような変化が起こっているのかわかります。
例えば以下のように、面積\(S\)、極板間の距離\(d\)、誘電率\(ε\)、電気量\(Q\)のコンデンサーに対して、面積\(S\)、高さ\(\displaystyle\frac{2d}{3}\)の金属板を挿入する場面を考えましょう。
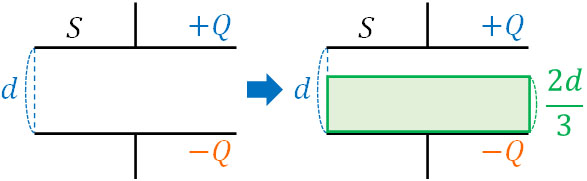
導体を挿入する前の電気容量を\(C\)とすると、静電エネルギーの公式より以下のようになります。
- \(U=\displaystyle\frac{Q^2}{2C}\)
それでは、導体挿入後の静電エネルギーはどのように変化するのでしょうか。前述の通り、電気容量の公式は\(C=ε\displaystyle\frac{S}{d}\)です。導体(金属板)の挿入により、極板間の距離は\(\displaystyle\frac{d}{3}\)になるため、以下のように導体挿入後の電気容量\(C’\)を計算しましょう。
\(C’=ε\displaystyle\frac{S}{\displaystyle\frac{d}{3}}\)
\(C’=ε\displaystyle\frac{3S}{d}\)
こうして、電気容量は\(C’=ε\displaystyle\frac{3S}{d}\)になるとわかります。言い換えると、電気容量は3倍になります。そこで静電エネルギーの公式へ代入すると、導体挿入後の静電エネルギー\(U’\)は以下のようになります。
\(U’=\displaystyle\frac{Q^2}{2C’}=\displaystyle\frac{Q^2}{6C}\)
こうして、導体を入れた後の静電エネルギーは\(U=\displaystyle\frac{Q^2}{6C}\)へ減少することがわかりました。電気量\(Q\)は変化しないものの、電位差\(V\)と電気容量\(C\)は変化するため、静電エネルギーは減少するのです。
外力による仕事\(W\)を計算する
それでは、減少したエネルギーはどこへ消えたのでしょうか。力学ではエネルギー保存則を学びます。エネルギー保存則は電気でも適用させることができ、前後でエネルギーの合計は同じになります。
金属をコンデンサー内に入れるためには力が必要です。つまり、あなたが力を加えて金属(導体)を移動させるのです。あなたが外力を加える必要があるため、その分だけ仕事をすることになります。
外力による仕事\(W\)により、その分だけ静電エネルギーは低くなります。エネルギー保存則により、仕事を行う前後でエネルギーの総量は以下のようになります。
- 操作前の静電エネルギー\(U\)+ 外力による仕事\(W\) = 操作後の静電エネルギー \(U’\)
なお先ほどの例題であれば、導体挿入前の静電エネルギー\(U\)と導体挿入後の静電エネルギー\(U’\)は以下のように既に計算しています。
- \(U=\displaystyle\frac{Q^2}{2C}\)
- \(U’=\displaystyle\frac{Q^2}{2C’}=\displaystyle\frac{Q^2}{6C}\)
そこで、以下のように外力による仕事\(W\)を計算しましょう。
\(U+W=U’\)
\(\displaystyle\frac{Q^2}{2C}+W=\displaystyle\frac{Q^2}{6C}\)
\(W=-\displaystyle\frac{Q^2}{3C}\)
こうして、あなたが金属板をコンデンサー内に挿入するとき、行う仕事(外力による仕事)は\(W=-\displaystyle\frac{Q^2}{3C}\)になるとわかります。
コンデンサーによる静電気力と外力による力の向き
それでは、金属板にはどのような向きで力が加わっているのでしょうか。また、あなたは金属板に対してどのような向きで力を加えたのでしょうか。
物理ではベクトル(向き)も重要です。そこで、図を利用してコンデンサーによる静電気力と外力による力の向きを考えましょう。例えば、以下のように、あなたは左向きで金属をコンデンサー内に挿入するとします。
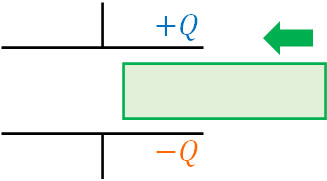
つまり左向きに力を加える場合、正の値になります。先ほどの計算結果より、\(W=-\displaystyle\frac{Q^2}{3C}\)です。\(W=Fx\)であるため、答えが負の値の場合、力のベクトルは右向きです。つまりあなたが金属(導体)をコンデンサー内に挿入するとき、右向きの力で引っ張る必要があります。
一方、コンデンサーには電荷が存在するため電場が発生しており、静電気力(クーロン力)が存在します。同じスピードで金属をコンデンサー内に挿入する場合、静電気力と外力はつり合います。外力(右向きの力)とつり合う必要があるため、静電気力(コンデンサーによる力)は左向きに働きます。
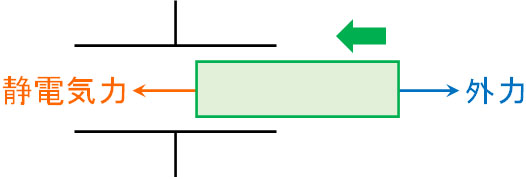
つまり、荷電しているコンデンサーに対して導体を左向きに挿入する場合、コンデンサーによる影響によって、導体(金属)はコンデンサー内に吸い込まれます。これはつまり、コンデンサーによる静電気力によって左向きの力が発生していることを意味しています。
そこで、コンデンサー内に吸い込まれる力に抵抗するように、あなたは力を右向きに加えるのです。これが、仕事\(W\)が負の値になる理由です。また、計算によってそれぞれの力の向きがわかります。
なお金属を挿入するときの例を利用して計算しましたが、金属をコンデンサー内から引き抜くときは逆の方法によって計算しましょう。考え方は同じなので、金属の挿入と引き抜きの両方で答えを得られるようになりましょう。
ジュール熱を含めるエネルギー保存の式
なお電気を学ぶとき、ジュール熱も考慮しなければいけません。仕事をすることによって静電エネルギーが変化するとき、ジュール熱が発生するケースも多いです。
先ほどの例では、ジュール熱が発生しない場合について計算の方法を解説しました。導体をコンデンサー内に挿入するとき、ジュール熱\(J\)を含めるのであれば、エネルギー保存の式は以下のようになります。
- 操作前の静電エネルギー\(U\)+ 外力による仕事\(W\) = 操作後の静電エネルギー \(U’\) + 発生するジュール熱\(J\)
ジュール熱の発生がない場合、ジュール熱を省いて計算しましょう。一方でジュール熱が発生する場合、ジュール熱を考慮しましょう。
導体を利用するときの距離、電圧、静電エネルギー、仕事を計算する
電荷が蓄積しているコンデンサー内に金属(導体)を挿入するケースがあります。この場合、電荷量と電場に変化はありません。一方で極板間の距離は金属の厚みの分だけ短くなり、電位差は低くなります。
このとき、挿入する金属がコンデンサーの面積よりも小さい場合、コンデンサーが並列接続されているとみなして計算しましょう。
また電位差が変わるため、導体の挿入によって静電エネルギーが変化します。つまり、外力は仕事をすることになります。そこで、静電エネルギーの変化を利用して外力による仕事を計算できるようになりましょう。
コンデンサー内部に金属を挿入する(または、コンデンサー内部から金属を引き抜く)ことにより、どのような変化が起こるのか学びましょう。これにより、極板間の距離や電圧、静電エネルギー、仕事の計算を行えるようになります。






