ギターなどの弦楽器では、弦を弾くことによって音が出ます。またトランペットやフルートなどの管楽器についても、音を出すことができます。また、これらの楽器では音を変えることができます。
それでは、これらの楽器を利用して演奏するとき、どのようにして音色が決まるのでしょうか。例えば、ギターの弦を押さえると高い音が出るのはなぜなのでしょうか。
弦は振動しますし、音も振動によって伝わります。つまり、これらは波で考えることができます。弦が振動することで定常波を作り、結果として楽器は音を作り出すことができるのです。
生じる定常波の波長や弦の長さ、波の速さ、振動数を確認することによって、これらの物理現象を理解できるようになります。そこで、弦に生じる定常波について、実際の物理現象と比較して説明していきます。
もくじ
弦の固定振動:基本振動と\(n\)倍振動の違い
弦を弾くと、音が鳴ります。音が鳴っているとき、必ず弦は振動しています。弦では、必ず両端が固定されています。つまり両端で波の固定端反射が起こります。こうして2つの波が重なり、定常波を作ります。
なお弦では両端が固定端反射になるため、両端は必ず節になります。

弦を弾くときに現れるこのような振動を弦の固有振動といいます。定常波が作られるとき、両端が節になるのが弦の固有振動です。また、このときの振動数を固有振動数といいます。
なお、どのように弦を振動させるのかによって、定常波の形が変わります。弦の場合、腹が一つだけであり、最もシンプルな振動を基本振動といいます。一方、基本振動が2つある場合は2倍振動といいます。また基本振動が3つ存在する場合、3倍振動といいます。
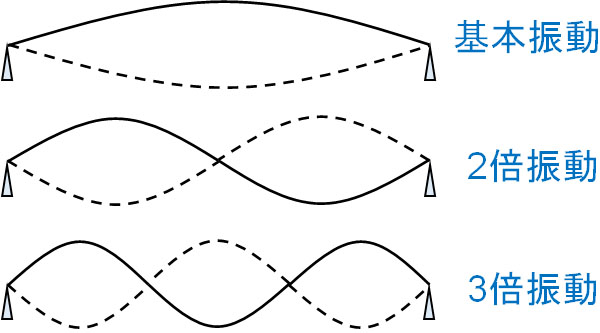
振動によって定常波が作られるとき、最も小さい単位が基本振動です。ただ定常波が作られるとき、基本振動が複数作られることもあるのです。このとき、基本振動が\(n\)個存在する振動を\(n\)倍振動といいます。
弦の長さ\(l\)と波長\(λ\)を表す式
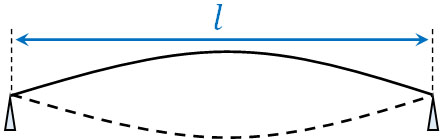
それでは、弦の長さ\(l\)と波長\(λ\)を利用して式を作りましょう。基本振動での弦の長さに着目すると、式を作ることができます。
基本振動では、弦の長さ\(l\)は波長の半分となっているので\(\displaystyle\frac{λ}{2}\)と表すことができます。また、基本振動の長さは弦の長さ\(l\)と一致しています。つまり、以下の式を作れます。
- \(l=\displaystyle\frac{λ}{2}\)
それでは、2倍振動や3倍振動ではどのような式になるでしょうか。弦の長さ\(l\)は同じであるものの、2倍振動や3倍振動では波長\(λ\)が変わります。そのため、以下の式になります。
- 2倍振動:\(l=λ\)
- 3倍振動:\(l=\displaystyle\frac{3}{2}λ\)
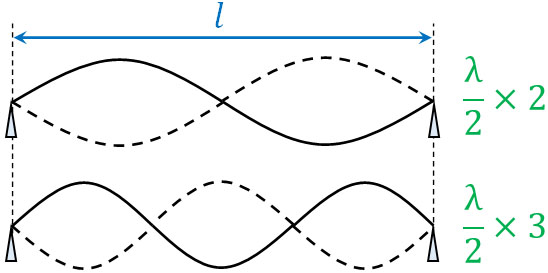
こうして、それぞれのケースで弦の長さ\(l\)と波長\(λ\)の関係を表すことができました。
固有振動数を速さ\(v\)で表す
また\(v=fλ\)であるため、\(λ=\displaystyle\frac{v}{f}\)です。そこで、基本振動の式に代入しましょう。
\(l=\displaystyle\frac{λ}{2}\)
\(l=\displaystyle\frac{v}{2f}\)
\(f=\displaystyle\frac{v}{2l}\)
こうして、基本振動での振動数を得ることができました。\(f=\displaystyle\frac{v}{2l}\)が基本振動での固有振動数です。なお、同様に計算すると固有振動数は以下のようになります。
- 基本振動:\(f=\displaystyle\frac{v}{2l}\)
- 2倍振動:\(f=\displaystyle\frac{v}{l}\)
- 3倍振動:\(f=\displaystyle\frac{3v}{2l}\)
つまり\(n\)倍振動では、固有振動数は以下のようになります。
- \(f=\displaystyle\frac{v}{2l}n\)
この公式を覚える必要はありません。図を利用することにより、式を作ることができるからです。
なお弦の長さが分母にあるため、弦の長さは振動数に関係していることがわかります。つまり弦が長いほど振動数は小さくなり、音が低くなります。またギターの弦を手で押さえると、押さえた部分が固定端となり、弦が短くなることで振動数は大きくなります。こうして、高い音を出すことができます。
物理で振動数を計算することにより、楽器の仕組みがわかります。物理を学ぶことで、自然現象が起きている理由を理解できるようになるのです。
弦を伝わる速さ\(v\)を表す公式
次に、弦を伝わる速さ\(v\)を表す公式を覚えましょう。弦を伝わる速さ\(v\)は、弦の張力\(S\)Nと線密度\(ρ\)kg/mを利用することにより、以下の公式で表すことができます。
- \(v=\sqrt{\displaystyle\frac{S}{ρ}}\)
高校物理では、この公式は覚えてしまって計算で利用するといいです。本来、物理で公式の暗記をするのは好ましくありません。ただこの公式については、公式を得る過程が複雑なので暗記するのです。
なお弦楽器では、弦の張力を強くするほど音が高くなります。これは、弦の張力が強いと波が速くなり、結果として振動数が大きくなるからです。
また同じ張力であっても、太い弦(線密度の大きい弦)では音が低くなります。公式を見てわかる通り、線密度が大きいと波のスピードは遅くなります。つまり振動数が小さくなり、低い音になるのです。
弦の振動に関わる練習問題
それでは、公式を利用して弦に生じる定常波の問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 綿密度\(ρ\)の弦に電磁音さを下図のようにつけ、弦の長さが\(l\)になるように調節し、質量\(m\)の重りを付けました。弦を振動させると、腹が3つの定常波ができました。なお、重力加速度を\(g\)とします。
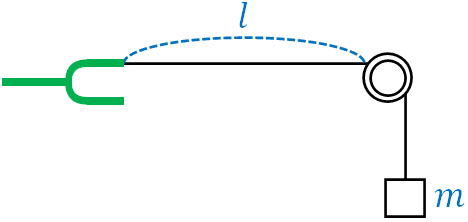
- 電磁音さの振動数を求めましょう。
- 質量\(M\)の重りを加えると、定常波の腹が2つになりました。振動数が同じ場合、\(M\)は\(m\)の何倍でしょうか。
1) 電磁音さの振動数を求めましょう
腹が3つであるため、以下の図を作れます。
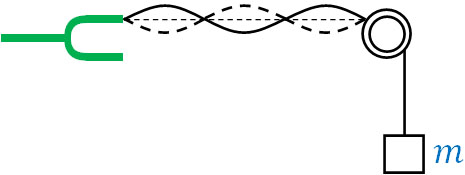
そこで、弦の長さ\(l\)と波長\(λ\)を利用すると、以下の式を作れます。
\(l=\displaystyle\frac{3}{2}λ\)
\(v=fλ\)より、\(λ=\displaystyle\frac{v}{f}\)なので、式を以下のように変形しましょう。
\(l=\displaystyle\frac{3}{2}λ\)
\(l=\displaystyle\frac{3v}{2f}\)
\(f=\displaystyle\frac{3v}{2l}\)
また力のつり合いより、張力\(S\)は\(mg\)です。そこで波の速さを得る公式を利用し、以下の式を作りましょう。
\(v=\sqrt{\displaystyle\frac{S}{ρ}}\)
\(v=\sqrt{\displaystyle\frac{mg}{ρ}}\)
そこで、\(v=\sqrt{\displaystyle\frac{mg}{ρ}}\)を\(f=\displaystyle\frac{3v}{2l}\)に代入しましょう。
\(f=\displaystyle\frac{3v}{2l}\)
\(f=\displaystyle\frac{3}{2l}\sqrt{\displaystyle\frac{mg}{ρ}}\)
こうして、振動数を得ることができました。
2) 質量\(M\)の重りを加えると、定常波の腹が2つになりました。振動数が同じ場合、\(M\)は\(m\)の何倍でしょうか
質量\(M\)の重りが加わり、定常波の腹が2つになるため、以下の図を作ることができます。

先ほどと同じように、弦の長さ\(l\)と波長\(λ\)を利用して式を作りましょう。
\(l=λ\)
\(λ=\displaystyle\frac{v}{f}\)より、以下の式になります。
\(l=\displaystyle\frac{v}{f}\)
\(f=\displaystyle\frac{v}{l}\)
振動数は同じであるため、\(f=\displaystyle\frac{3}{2l}\sqrt{\displaystyle\frac{mg}{ρ}}\)を利用し、式を以下のように変えましょう。
\(f=\displaystyle\frac{v}{l}\)
\(\displaystyle\frac{3}{2l}\sqrt{\displaystyle\frac{mg}{ρ}}=\displaystyle\frac{v}{l}\)
\(\displaystyle\frac{3}{2}\sqrt{\displaystyle\frac{mg}{ρ}}=v\)
なお、張力\(S\)は\((m+M)g\)です。そのため、速さ\(v\)を以下のように表すことができます。
\(v=\sqrt{\displaystyle\frac{(m+M)g}{ρ}}\)
そこで、\(v=\sqrt{\displaystyle\frac{(m+M)g}{ρ}}\)を代入しましょう。
\(\displaystyle\frac{3}{2}\sqrt{\displaystyle\frac{mg}{ρ}}=v\)
\(\displaystyle\frac{3}{2}\sqrt{\displaystyle\frac{mg}{ρ}}=\sqrt{\displaystyle\frac{(m+M)g}{ρ}}\)
\(\displaystyle\frac{9}{4}m=m+M\)
\(M=\displaystyle\frac{5}{4}m\)
こうして、\(M\)の質量は\(m\)の\(\displaystyle\frac{5}{4}\)倍とわかります。
弦に生じる定常波の特徴を知る
波を理解すると、楽器を利用して音を出すときの原理がわかります。楽器で弦が利用されることは多く、ギターなどの弦楽器では両端が固定されているため、固定端反射によって定常波が生まれます。そこで、弦に生じる定常波の性質を学びましょう。
両端で固定端反射するため、弦の両端は必ず節になります。また腹の数によって、基本振動、2倍振動、3倍振動と波長の長さが変わります。そこで弦の長さを利用し、式を作れるようにしましょう。また波長に関する公式を利用し、振動数を計算できるようになりましょう。
弦に生じる定常波の式を利用すれば、なぜ弦が短いと高い音を生じるのかわかります。また太い弦では、なぜ音が低くなるのかわかります。こうした物理現象は数式で説明できるのです。
弦の固有振動や\(n\)倍振動の内容を理解し、公式を利用して式を作れるようになりましょう。定常波の性質を利用することにより、弦に生じる定常波の計算問題を解けるようになります。






