物理では宇宙を取り扱います。私たちの身近で発生している物理現象だけでなく、力学を学ぶことによって惑星の軌道を計算できるようになるのです。
惑星の軌道を理解するとき、重要な法則にケプラーの法則があります。ケプラーの法則には3つあり、それぞれの法則の意味を覚えましょう。
万有引力を学ぶ前に理解しなければいけない内容がケプラーの法則です。ケプラーの法則を理解することにより、惑星の軌道に関する性質がわかるのです。
それでは、ケプラーの法則はどのような内容なのでしょうか。また、ケプラーの法則にはどのような公式があるのでしょうか。ここではそれぞれのケプラーの法則について、詳細や公式の意味を解説していきます。
もくじ
万有引力で重要なケプラーの法則
ドイツの天文学者であるケプラーが発見した惑星に関する法則がケプラーの法則です。惑星の軌道や衛星の速さを計算するためには、ケプラーの法則と万有引力の二つを理解する必要があります。
ケプラーの法則は3つあり、それぞれ内容が異なります。彼が発見した法則は以下の通りです。
- ケプラーの第一法則:惑星は太陽を一つの焦点として楕円軌道を描く
- ケプラーの第二法則:惑星と太陽を結ぶ線分について、特定の時間内での面積は一定
- ケプラーの第三法則:惑星の公転周期の2乗は、軌道長半径の3乗に比例する
恐らく意味を理解できないと思いますので、以下で詳細を解説していきます。
ケプラーの第一法則:惑星の軌道は楕円になる
ケプラーの第一法則と第二法則は内容が簡単です。まずケプラーの第一法則とは、要は「惑星は楕円軌道を描く」という法則です。
任意の2点(焦点)からの距離の和が一定になるように線を引く場合、楕円になります。円は2つの焦点が重なっています。円は楕円の一種なのです。2つの焦点が重なっていない場合、円ではなく楕円になります。
惑星にとって、太陽は焦点です。また、ほかの部分にもう一つの焦点が存在しており、結果として惑星は楕円軌道を描きます。
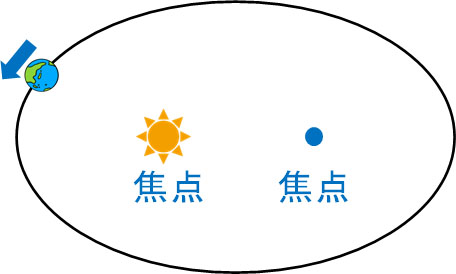
「惑星の軌道は楕円になる」という法則がケプラーの第一法則です。
ケプラーの第二法則:特定時間での面積は等しい
次にケプラーの第二法則を学びましょう。惑星は太陽の周りを公転しています。例えば惑星が1日かけて点Pから点P’へ移動したとします。また異なる時刻について、惑星が1日かけて点Qから点Q’へ移動したとします。
太陽の位置を点Oとすると、惑星が描いたPOP’の面積S1とQOQ’の面積S2は同じです。
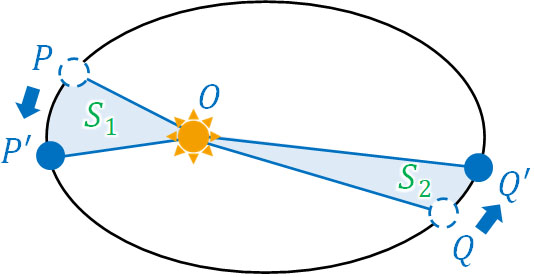
それでは、惑星と太陽との距離を\(r\)、惑星の速さを\(v\)、惑星と太陽を結ぶ線分と速さの方向との角度をθとしましょう。
経過時間が短い場合、惑星は直線運動をしており、太陽と惑星の軌道を結ぶことによって三角形を作ることができます。惑星の軌道は楕円であるため、実際には直線ではありません。ただ経過時間が短い場合、ほぼ直線と同じであるため、惑星の動きを直線とみなすのです。
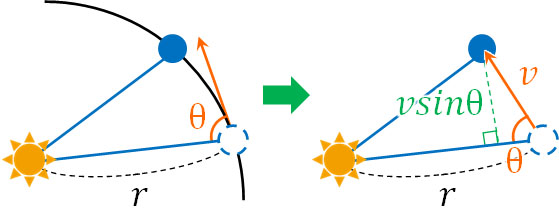
横の長さは\(r\)であり、たての長さは\(vsinθ\)です。そのため、三角形の面積は\(\displaystyle\frac{1}{2}rvsinθ\)となります。
長軸上に惑星がある場合、三角形の面積によって計算できる
それでは、少し特殊なケースを確認しましょう。惑星軌道では、2つの焦点を通る線分を長軸といいます。仮に長軸上に2つの惑星がある場合、三角形の角度θは\(\displaystyle\frac{π}{2}\)(90°)となります。つまり、\(sinθ=1\)となります。
惑星と太陽との距離がそれぞれ\(r\)と\(R\)、惑星の速さが\(v\)と\(V\)の場合、以下の式を作ることができます。
- \(\displaystyle\frac{1}{2}rv=\displaystyle\frac{1}{2}RV\)
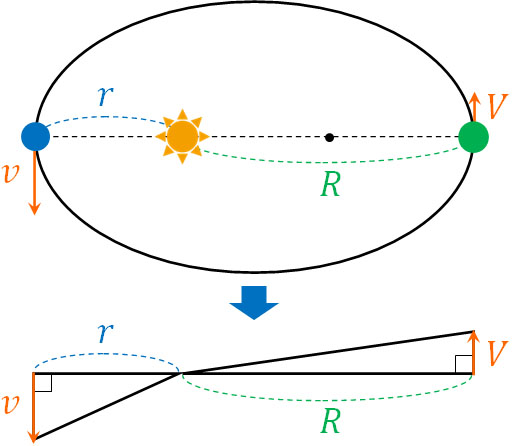
これがケプラーの第二法則です。ケプラーの第二法則についても、理解すれば内容は難しくないとわかります。
・ケプラーの第二法則を利用する計算問題
それでは上図について、速さ\(v\)は速さ\(V\)の何倍でしょうか。この問題を解くため、ケプラーの第二法則を利用して以下の計算をしましょう。
\(\displaystyle\frac{1}{2}rv=\displaystyle\frac{1}{2}RV\)
\(v=\displaystyle\frac{R}{r}V\)
こうして、速さ\(v\)は速さ\(V\)を\(\displaystyle\frac{R}{r}\)倍することで得られるとわかります。
ケプラーの第三法則:惑星の公転周期と楕円の軌道長半径(半長軸)の関係
ケプラーの第三法則では、惑星の公転周期と楕円の軌道長半径(半長軸)を利用します。太陽の周りを惑星は回っており、公転周期が存在します。例えば地球の公転周期は1年です。
このとき公転周期\(T\)を二乗すると、軌道長半径\(a\)の3乗に比例することがわかっています。比例定数を\(k\)とすると、以下の式によって表されます。
- \(T^2=ka^3\)
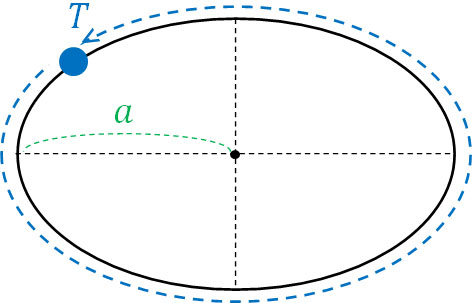
なお\(k\)は定数であるため、以下のように表すこともできます。
- \(\displaystyle\frac{T^2}{a^3}=\)一定
焦点が同じ惑星の場合、\(k\)の値は同じです。万有引力の計算では、ケプラーの法則を利用するケースがひんぱんにあります。楕円軌道の計算では、\(T^2=ka^3\)を利用して答えを得るのです。
ケプラーの第一法則と第二法則を利用する練習問題
それでは、ケプラーの法則を利用して物理の問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 太陽と惑星の軌道について、公転速度が最大となるときの惑星と太陽の位置関係は以下のうち、どれでしょうか。
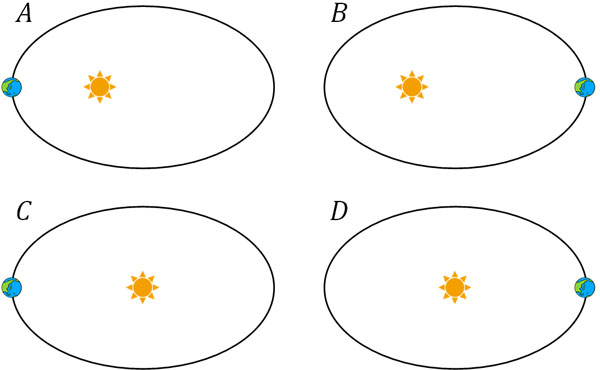
ケプラーの第一法則より、太陽は楕円の焦点に該当します。そのため、CとDは誤りです。それではAとBのうち、どちらのほうが公転速度が速いでしょうか。
ケプラーの第二法則より、特定の時間あたりに惑星が描く面積は一定です。太陽に近いと、横軸が短くなるので、その分だけたて軸(速さ)の値は大きくなります。一方で太陽から遠いと横軸が長くなり、その分だけたて軸(速さ)の値は小さくなります。そのため、正解はAです。
ケプラーの第三法則を利用し、公転周期を得る
ケプラーの法則は太陽の周囲を公転している惑星だけでなく、惑星の周囲を回っている衛星にも適用できます。そこで、以下の問題を解いてみましょう。
- 土星の衛星としてパンとレアが知られています。土星中心からの平均距離(軌道長半径)は、パンは土星半径に対して2.2倍、レアは土星半径に対して8.8倍です。レアの公転周期はパンの公転周期の何倍でしょうか。
ケプラーの第三法則を利用して計算しましょう。土星に対するパンの軌道長半径を\(a\)とすると、土星に対するレアの軌道長半径は\(4a\)です。
そこでパンの公転周期を\(T\)、レアの公転周期を\(T’\)としましょう。パンとレアは同じ焦点(土星)を利用しています。そのためケプラーの第三法則での比例定数\(k\)は一定です。つまり、以下の式を作ることができます。
\(\displaystyle\frac{T^2}{a^3}=\displaystyle\frac{T’^2}{(4a)^3}\)
\(\displaystyle\frac{T^2}{a^3}=\displaystyle\frac{T’^2}{64a^3}\)
\(64T^2=T’^2\)
\(T’=8T\) (\(T’>0\))
こうして、レアの公転周期\(T’\)はパンの公転周期\(T\)の8倍であると計算できました。焦点が同じ場合、ケプラーの第三法則を利用することによって公転周期の計算が可能です。
ケプラーの法則を利用し、惑星や衛星の軌道を計算する
宇宙に関する法則がケプラーの法則です。ケプラーの法則には3つの種類があり、教科書に記載されている説明は難解です。
ただ詳細を確認すると、難しくないことがわかります。ケプラーの第一法則は「惑星は太陽を焦点として楕円軌道を描く」という法則です。
またケプラーの第二法則は「一定期間に動く惑星と太陽を結ぶ面積は等しくなる」という法則です。ケプラーの第二法則を利用することにより、惑星(または衛星)の速さを計算できます。
ケプラーの第三法則は、公転周期と軌道長半径(半長軸)の関係性を表しています。\(T^2=ka^3\)となることを覚えましょう。これらケプラーが発見した法則を学ぶことにより、惑星の軌道や速さの計算が可能になります。






