コンデンサーを含む直流回路：抵抗と回路の関係

回路の問題では、コンデンサーを含むケースが多いです。そこで、コンデンサーと抵抗を含む直流回路について、計算できるようになりましょう。

コンデンサーが回路に存在する場合、2パターンが存在します。一つはスイッチを入れた直後の状態です。もう一つはスイッチを入れた後、十分な時間が経過した後の状態です。それぞれの状態はまったく異なります。

つまり直流回路でコンデンサーを含む場合、どちらの状態なのかを見極めなければいけません。コンデンサーの状態によって、回路に対する影響はまったく異なります。

それでは、直流回路にコンデンサーを含む場合はどのように式を作ればいいのでしょうか。直流回路にコンデンサーと抵抗を含む場合の計算方法を解説していきます。

1 コンデンサーを含む回路は2パターンで考える
2 充電時に起こるコンデンサーを含む回路での現象
3 放電時に起こるコンデンサーを含む回路での現象
4 直流回路にコンデンサーを含む場合、回路を簡略化する

コンデンサーを含む回路は2パターンで考える

直流回路にコンデンサーが接続されている場合、出題される問題は以下の2パターンです。

スイッチを入れた直後の様子
スイッチを入れ、十分に時間が経過した後の様子

高校物理などで電気の初歩を学ぶとき、\(t\)秒後の回路の状態が問われることはありません。電源を入れた後、時間経過と共に回路の電流は変化します。また、コンデンサーに蓄積される電気量は増えます。

ただ、これらの計算をするためには微分を利用しなければいけません。そのため大学では学ぶものの、高校物理では2パターンの問題のみなのです。そのため、コンデンサーを含む計算問題はシンプルです。問題の解き方を理解すれば、容易に式を作ることができます。

充電時に起こるコンデンサーを含む回路での現象

それでは、実際にどのような現象が起こるのか確認しましょう。まず、電源とつなぐことでコンデンサーを充電する場面を考えましょう。

充電するとき、以下の2パターンを考えます。

電源につないだ直後：コンデンサーを導線とみなす
電源につなぎ、十分な時間が経過した：コンデンサーで断線される

つまり、コンデンサーへの充電開始直後とコンデンサーへの充電が完了した後では、回路の様子が大きく変化します。

充電時、電源につないだ直後の回路

コンデンサーは電荷の蓄積が可能です。そのためコンデンサーに電荷がゼロの場合、電源とつなぐことで電流が流れ、コンデンサーに電荷が溜まっていきます。

このとき、コンデンサーに存在する自由電子は負極板へ移動します。同時に、電子の向きとは反対方向に電流が流れます。

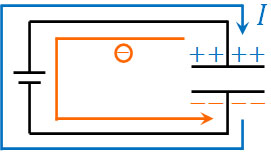
つまり電源につないだ直後というのは、コンデンサーが存在しない状態と同じです。コンデンサーがあってもなくても、電源による起電力\(V\)によって電流\(I\)が流れます。

そのため直流回路にコンデンサーと抵抗が存在する場合、電源につないだ直後では、以下のように「コンデンサーは回路に存在しない」と考えましょう。

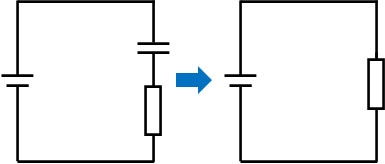
コンデンサーを導線とみなすことにより、回路の構造をシンプルにできます。コンデンサーのない回路を考えればいいため、オームの法則や合成抵抗を利用することによって電圧や電流を計算できます。

電源につなぎ、十分な時間が経過した後は電流が遮断される

一方、電源につないだあとに十分な時間が経過した後はどのようになるのでしょうか。コンデンサーへの充電が完了した後、電流が流れないことは既に知っていると思います。十分な時間が経過した後、電源の起電力とコンデンサーの電位差は同じになります。

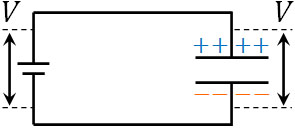
電圧が等しい場合、電流が流れることはありません。そのため十分な時間が経過した後では、コンデンサーが存在する部分は断線していると考えることができます。

例えば以下の回路では、十分な時間が経過した後は以下のように回路を書き直すことができます。

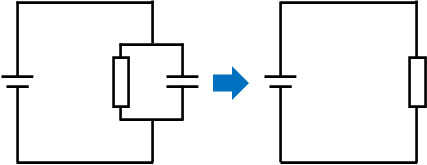
コンデンサーの部分で断線しているため、電気は通りません。そこで、コンデンサーにつながっている導線を消去しましょう。こうして、先ほどと同様に回路を単純化させることができます。

電流の大きさと電気量の時間変化

それでは、電源とつないだ後の電流\(I\)とコンデンサーに蓄積している電気量\(Q\)について、時間変化のグラフを確認しましょう。

横軸を時間\(t\)とすると、以下のようになります。

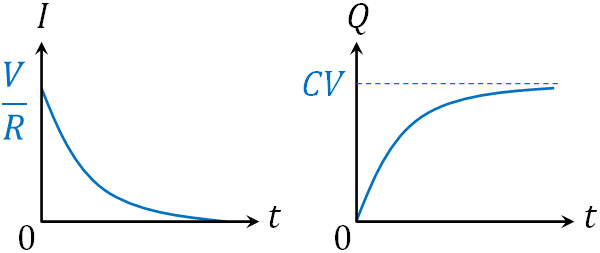
最終的に電流がゼロになるため、当然ながら時間経過と共に電流\(I=\displaystyle\frac{V}{R}\)の値は小さくなります。電源につないだ直後は電源の起電力によって電流が発生するものの、コンデンサーに電気量が蓄積するに従い、電流が弱くなるのです。

コンデンサーというのは、値の変化する抵抗と考えることができます。コンデンサーに電荷がない場合、抵抗は0なので電流が流れやすいです。一方で十分な時間が経過すると、抵抗の値は無限大に大きくなります。なお当然ながら、十分な時間が経過した後、電気量\(Q\)は\(Q=CV\)となります。

放電時に起こるコンデンサーを含む回路での現象

コンデンサーは充電ができる一方、放電することもできます。そこで、放電時についても接続直後と十分に時間が経過した後の2パターンを考えましょう。

回路につないだ直後：コンデンサーを電源とみなす
回路につなぎ、十分な時間が経過した：コンデンサーを導線とみなす

先ほどと同じように、それぞれのパターンを確認しましょう。

回路へ接続直後、コンデンサーを電源とみなせる

充電したコンデンサーには、電気量\(Q\)が存在します。そのためコンデンサーを回路へ接続する場合、コンデンサーを電源とみなすことができます。コンデンサーは電源ではないものの、回路へ接続した直後は起電力\(V\)の電源と役割が同じです。

例えば下図について、電源とつながるスイッチを閉じて十分に時間が経過した後、このスイッチを切った場合、コンデンサーは新たな電源としての役割を果たします。

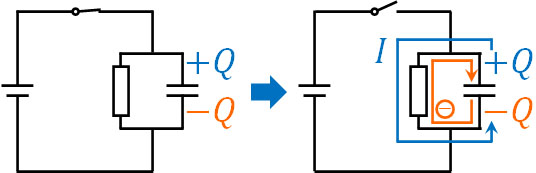
この回路の場合、元の電源とつながるスイッチを閉じて十分に時間が経過した後、コンデンサーは元の電源と同じ電圧\(V\)となります。そのため、スイッチを切った瞬間はコンデンサーが新たな電源となり、電圧\(V\)によって電流\(I\)が流れるのです。

電圧\(V\)と抵抗\(R\)の値は既にわかっているため、オームの法則を利用することにより、電流\(I\)を計算できます。

十分な時間経過の後、コンデンサーは導線とみなせる

一方、スイッチを切って十分な時間が経過したあとは、どのように考えればいいのでしょうか。放電により、時間経過と共にコンデンサーに蓄積している電気量は少なくなります。当然、時間経過と共に電流\(I\)も弱くなります。

こうして、最終的に電流は流れなくなります。コンデンサーに蓄積している電気量がなくなり、中性になると、電位差がゼロになります。当然、電位差がゼロの場合は電流が流れることはありません。

放電が完了したら、最初の状態に戻ります。コンデンサーに電荷がない場合、電源に接続直後では、コンデンサーを導線とみなすことができました。同様に、放電によって十分な時間が経過した後なのであれば、コンデンサーを導線とみなしましょう。コンデンサーに電荷が存在しない事実は同じだからです。

例えば先ほどの回路であれば、放電によって十分な時間が経過した後、以下のように回路を変形しましょう。

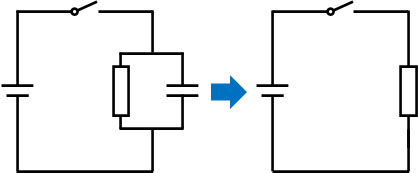
このように放電完了後では、コンデンサーには電荷が存在せず、抵抗はゼロです。そのため、コンデンサーを導線とみなして問題ありません。

コンデンサーを含む直流回路の練習問題

それでは、実際に練習問題を解いてみましょう。以下の問題の答えは何でしょうか。

電圧\(V\)の電源に対して、下図のように抵抗値が\(R\)と\(2R\)の抵抗、電気容量\(C\)のコンデンサーがあります。最初、コンデンサーに電荷はありません。

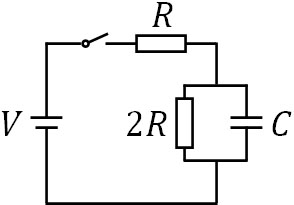
スイッチを閉じた直後、それぞれの抵抗に流れる電流はいくらですか。
スイッチを閉じて十分な時間が経過した後、それぞれの抵抗に流れる電流はいくらですか。
(2)の後、スイッチを切った直後にそれぞれの抵抗に流れる電流はいくらですか。

1) スイッチを閉じた直後、それぞれの抵抗に流れる電流はいくらですか

スイッチを閉じた直後では、コンデンサーの抵抗はゼロです。そのためコンデンサーに加わる電圧は0であり、以下のように回路を書き換えることができます。

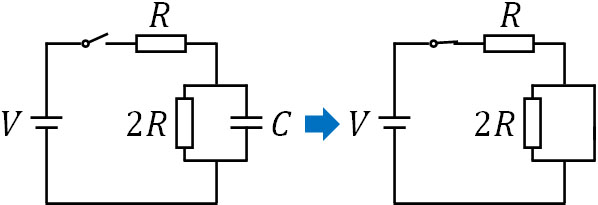
コンデンサーに加わる電圧が0であるため、並列接続となっている抵抗\(2R\)に加わる電圧も0です。つまり、抵抗\(2R\)に電流は流れません。これについては当然であり、抵抗を通るのではなく、抵抗のない導線を電流は通りたいと考えます。そのため計算しなくても、抵抗\(2R\)の電流は0とわかります。

またオームの法則より、\(V=RI\)です。そのため、抵抗\(R\)を流れる電流は\(I=\displaystyle\frac{V}{R}\)です。

2) スイッチを閉じて十分な時間が経過した後、それぞれの抵抗に流れる電流はいくらですか

スイッチを閉じて十分な時間が経過した後では、コンデンサーに電荷が蓄積しており、電流が通ることはありません。つまり、コンデンサーの部分で断線されていると考えることができます。そこで、以下のように回路を書き換えましょう。

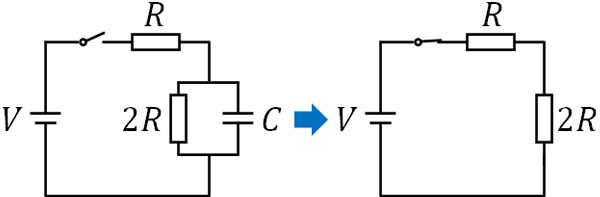
コンデンサーの部分で電流が遮断されているため、回路を書き直すとき、コンデンサーを省きましょう。なおキルヒホッフの第二法則を利用すると、以下の式を作れます。

\(V+(-RI)+(-2RI)=0\)

\(3RI=V\)

\(I=\displaystyle\frac{V}{3R}\)

こうして、それぞれの抵抗を流れる電流は\(I=\displaystyle\frac{V}{3R}\)とわかりました。なお直列接続であるため、抵抗を流れる電流の大きさは同じです。

3) (2)の後、スイッチを切った直後にそれぞれの抵抗に流れる電流はいくらですか

スイッチを切った直後では、コンデンサーは電源として働きます。そこで、以下のように回路を書き直しましょう。

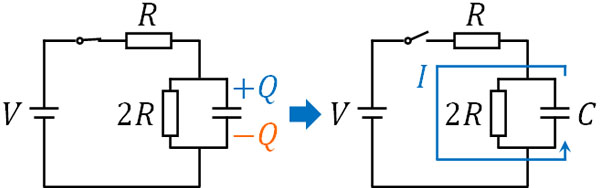
スイッチを切ると、当然ながらその部分は断線します。そのため、抵抗\(R\)を流れる電流はゼロです。そこで、抵抗\(2R\)に流れる電流を計算しましょう。

スイッチが入っている場合では、抵抗\(2R\)を流れる電流は\(I=\displaystyle\frac{V}{3R}\)であるため、オームの法則を利用し、以下のように抵抗\(2R\)に加わる電圧\(V’\)を計算できます。

\(V’=2R×\displaystyle\frac{V}{3R}\)

\(V’=\displaystyle\frac{2V}{3}\)

抵抗\(2R\)とコンデンサーは並列接続であるため、コンデンサーの電位差は\(V’=\displaystyle\frac{2V}{3}\)です。次に、コンデンサーを起電力\(V’=\displaystyle\frac{2V}{3}\)の電源とみなし、流れる電流を計算しましょう。オームの法則を利用すると、以下のように計算できます。

\(\displaystyle\frac{2V}{3}=2R×I\)

\(I=\displaystyle\frac{V}{3R}\)

こうして、抵抗\(2R\)を流れる電流は\(I=\displaystyle\frac{V}{3R}\)と計算できました。