光が反射をしたり、屈折したりすることは既に知っていると思います。ガラスや水面によって光が反射するのはすべての人が理解しています。また、光が水やガラスに入ると屈折します。
こうした現象を理解するためには、ホイヘンスの原理を学ばなければいけません。一つの波について、たくさんの点で構成されていると考えるのがホイヘンスの原理です。
また光が反射や屈折をするとき、角度や波長の変化を計算できるようになりましょう。計算するときは公式を暗記するのではなく、公式の意味を理解する必要があります。なお光の反射と屈折を学べば、光が全反射するときの角度を計算できます。
それでは、ホイヘンスの原理とは何なのでしょうか。また、どのように光の反射や屈折を計算すればいいのでしょうか。ここではホイヘンスの原理や光の反射と屈折、全反射、光の分散を解説していきます。
もくじ
ホイヘンスの原理と素元波
波の性質を学ぶとき、線(または曲線)を利用して理解します。そこで次は、波が線ではなく多くの点によって構成されていると考えましょう。
波のない水面に対して水滴を垂らすと、円形の波が作られます。また、円形の波は時間経過と共に大きくなります。

それでは、なぜ波は円状に広がるのでしょうか。この現象を説明するとき、ホイヘンスの原理を利用します。
ホイヘンスの原理では、一つの波がたくさんの点によって構成されていると考えます。また、それぞれの点を起点として、円状の波が広がっていきます。これが繰り返されることにより、円が大きくなっていきます。
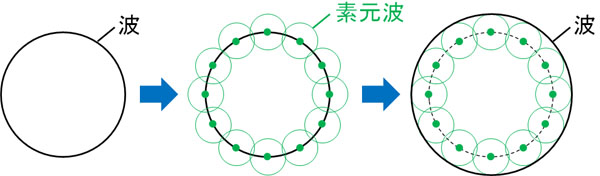
波面に存在する点から発生される波を素元波といいます。素元波が円形の波を作ることにより、波面が広がっていくのです。
波が回折する理由はホイヘンスの原理で説明できる
次は波が円形に広がる場面ではなく、波が直線で進む場面を考えましょう。この場合、ホイヘンスの原理を利用すると、以下のように波が進んでいきます。

波が直線で進む場合についても、ホイヘンスの原理を利用することによって図を作ることができます。
なおホイヘンスの原理を利用すれば、波が回折する理由を説明できます。波が障害物を過ぎた後、波が後ろに回り込んで進む現象を回折といいます。直線に進んでいた波が障害物の壁に到達するのは奇妙に思えますが、ホイヘンスの原理によって説明できるのです。
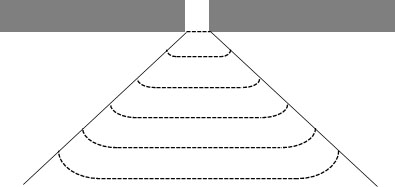
まず、狭いすき間を波が通過する場面を考えましょう。波はすき間を通過後、ホイヘンスの原理により、徐々に幅が広がっていきます。
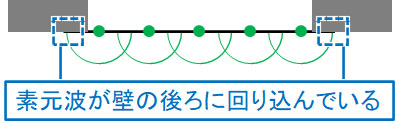
また素元波は円形であるため、波は壁にも到達します。波が壁を通過した直後では、以下のように、端に存在する素元波は壁に到達します。つまり、波は壁の裏側にも到達します。
すべての波がホイヘンスの原理に従います。そのため音や光など、波はホイヘンスの原理に従って進むと理解しましょう。
反射の法則と屈折の法則
それでは、光が反射するときの法則を確認しましょう。反射の法則は簡単であり、入射角と反射角が同じになります。入射角をθ1、反射角をθ2とすると、以下の関係が成り立ちます。
- \(θ_1=θ_2\)
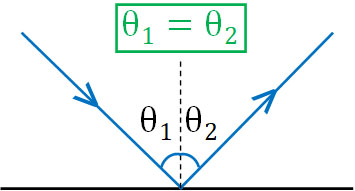
入射角と反射角が等しくなるのは、感覚的に多くの人が理解できると思います。
・屈折で利用されるホイヘンスの原理
次に屈折の法則を学びましょう。空気と水のように、異なる媒質の境目で光の向きが変わります。この現象を屈折といいます。光が垂直に水面に入る場合、光は曲がりません。しかし、水面に対して斜めに入射する場合、光は曲がるのです。
このとき、光が入るときの角度を入射角、屈折後の角度を屈折角といいます。
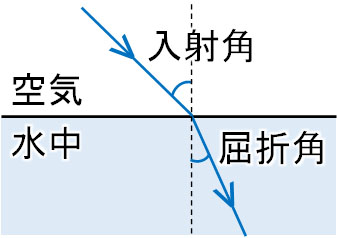
なぜ、光の屈折が起こるのかを説明するとき、ホイヘンスの原理が役立ちます。光が空気中を進むのと、水中を進むのでは速さが異なります。光の速さは、水中よりも空気中のほうが速いです。言い換えると、空気中よりも水中のほうが素元波の半径が小さくなります。
そこで、光を幅のある棒と捉えましょう。光が水中に入るとき、端が空気中から水中に入ると速度が遅くなります(素元波の半径が小さくなる)。一方で空気中にある光の端はスピードが速いです(素元波の半径が大きい)。そのため、光の角度が変化します。
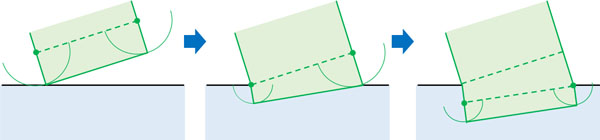
その後、両方の端が水中に入ると同じスピードで水中を進むことになります。両方の端で小さい素元波が作られるため、水中をまっすぐ進むのです。媒質(空気や水、ガラスなど)によって光の速度が変化するため、ホイヘンスの原理により、光は屈折するのです。
屈折率\(n\)と速さ\(v\)をかけると光の速度\(c\)になる
屈折を学ぶとき、重要な数字として屈折率(絶対屈折率)\(n\)があります。光が進む速度は真空中が最も早いです。そこで、真空を進む光の屈折率を1とします。光の速さが遅くなるほど屈折率は高くなり、例えば水の屈折率は約1.3であり、ダイヤモンドの屈折率は約2.4です。
また真空を進む光の速さを\(c\)、媒質1(水やガラスなど)を進む光の速さを\(v_1\)、媒質1の屈折率を\(n_1\)とすると、以下の公式が成り立ちます。
- \(c=n_1v_1\)
光が媒質1の中にある場合、必ず真空を進むときに比べて必ずスピードは遅くなります。ただ、同じ割合で屈折率が大きくなります。そこで遅くなったスピード\(v_1\)に対して、屈折率\(n_1\)をかけることにより、真空を進む光の速さ\(c\)になるのです。
公式を覚えても意味がなく、公式がもつ意味を理解しましょう。そうすれば、なぜ屈折率と速さをかける必要があるのか理解できます。
・真空を進む光の速さ\(c\)は定数
重要なのは、真空を進む光の速さ\(c\)は常に値が同じです。\(c\)は定数なのです。そのため媒質1や媒質2を通過する光には以下の関係が成り立ちます。
- \(n_1v_1=n_2v_2(=c)\)
速さと屈折率をかけると、必ず真空を進む光の速さ\(c\)になります。そのため、上記の公式が成り立ちます。
・振動数\(f\)は変化せず、波長\(λ\)が変化する
それでは、光の速さが変化する理由は何でしょうか。波の性質で学んだ通り、波の速さは\(v=fλ\)で表されます。つまり、光の速さは振動数\(f\)と波長\(λ\)に依存します。
波には独立性があるため、理由なく波が消えることはありません。つまり、媒質が変化しても振動数\(f\)は同じです。そのため光の速さが変わるというのは、波長\(λ\)が変化することを意味します。
そこで媒質1と媒質2について、それぞれの波長を\(λ_1\)と\(λ_2\)とするとき、\(v_1=fλ_1\)と\(v_2=fλ_2\)を代入しましょう。
\(n_1v_1=n_2v_2(=c)\)
\(n_1fλ_1=n_2fλ_2\)
\(n_1λ_1=n_2λ_2\)
こうして、公式として\(n_1λ_1=n_2λ_2\)を得ることができました。媒質による光の速さの変化が波長の変化によって起こる事実を学べば、なぜこの公式が成り立つのか理解するのは容易です。
・sinθを利用して公式を作る
次にsinθを利用して屈折に関する公式を作りましょう。以下のように、入射角が同じであるものの、入射場所が異なる2つの光を利用して図を作ります。
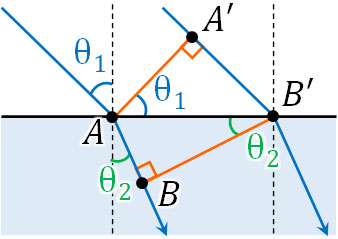
ABとA’B’は速さを表しています。つまり\(A’B’=v_1\)(媒質1を進む速さ)、\(AB=v_2\)(媒質2を進む速さ)となります。そこでAB’とsinθを利用すると、以下の式を作れます。
- \(sinθ_1=\displaystyle\frac{v_1}{AB’}\)
- \(sinθ_2=\displaystyle\frac{v_2}{AB’}\)
AB’は共通なので、2つの式を利用して以下のように変形しましょう。
- \(\displaystyle\frac{sinθ_1}{sinθ_2}=\displaystyle\frac{v_1}{v_2}\)
また速さと波長は比例するので以下の式を作れます。
- \(\displaystyle\frac{sinθ_1}{sinθ_2}=\displaystyle\frac{v_1}{v_2}=\displaystyle\frac{λ_1}{λ_2}\)
光の屈折では、以下のように図を利用して公式を覚えましょう。
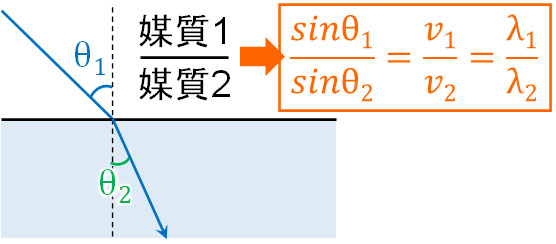
これにより、光の屈折を計算するときに公式を必ず思い出せるようになります。
屈折率は上下逆になる:相対屈折率の計算
なお注意点として、屈折率は先ほどの公式に対して上下逆さまになります。\(n_1v_1=n_2v_2(=c)\)より、\(\displaystyle\frac{v_1}{v_2}=\displaystyle\frac{n_2}{n_1}\)です。そのため、以下の関係になります。
- \(\displaystyle\frac{sinθ_1}{sinθ_2}=\displaystyle\frac{v_1}{v_2}=\displaystyle\frac{λ_1}{λ_2}=\displaystyle\frac{n_2}{n_1}\)
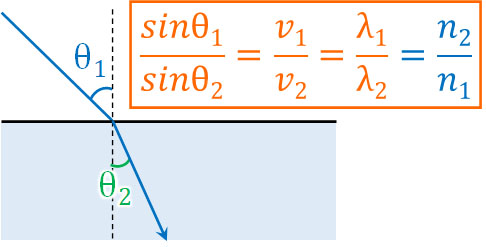
屈折率の部分だけ、分子と分母が反対になることに注意しましょう。なお屈折率と角度θに着目すると、以下の関係が成り立ちます。
- \(n_1sinθ_1=n_2sinθ_2\)
先ほどの公式を変形しただけですが、この式を確認すると、\(n_1v_1=n_2v_2(=c)\)と意味が同じと理解できます。
・相対屈折率の概念
なお、\(\displaystyle\frac{n_2}{n_1}\)を相対屈折率\(n_{12}\)といいます。
- \(\displaystyle\frac{n_2}{n_1}=n_{12}\)
真空ではない2つの媒質の屈折率を比較する値が相対屈折率です。媒質1に対する、媒質2の屈折率が相対屈折率\(n_{12}\)なのです。相対屈折率を含めると、公式は以下のようになります。
- \(\displaystyle\frac{sinθ_1}{sinθ_2}=\displaystyle\frac{v_1}{v_2}=\displaystyle\frac{λ_1}{λ_2}=\displaystyle\frac{n_2}{n_1}=n_{12}\)
真空と比較するため、絶対屈折率は必ず1より大きくなります。一方で相対屈折率では、値が1より大きくなることがあれば、小さくなることもあります。
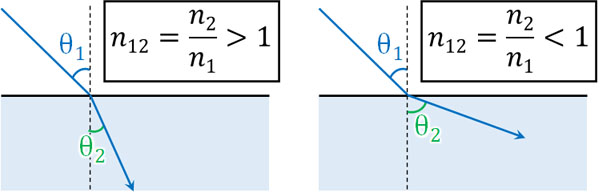
屈折率は一般的に絶対屈折率を指します。一方で「媒質1に対する媒質2の屈折率」という表記がある場合、相対屈折率\(n_{12}\)を指します。
屈折率を用いた練習問題
それでは、屈折率を活用した練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 厚さ5.0cmのガラス板を空気中に置きます。単色光を60°の角度で入射させたところ、反射光と屈折角のなす角は75°になりました。なお角θが極めて小さい場合、\(sinθ≒tanθ\)が成り立つとします。また、空気中の屈折率を1とします。
- ガラスの屈折率を求めましょう。
- このガラス板を真上から見る場合、厚さは何cmに見えるでしょうか。
1) ガラスの屈折率を求めましょう
まず、図を作りましょう。以下のようになります。
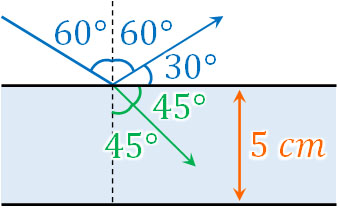
入射角がわかっているため、反射角は60°です。また反射光と屈折角のなす角は75°なので、図のようにそれぞれ30°と45°を図に記入しましょう。そうすると、屈折角は45°とわかります。
次に、屈折の法則に関わる公式を利用して計算しましょう。空気中の屈折率は1であり、入射角と屈折角がわかっているため、ガラスの屈折率を計算できます。
\(n_1sinθ_1=n_2sinθ_2\)
\(1×sin60°=n_2×sin45°\)
\(\displaystyle\frac{\sqrt{3}}{2}=n_2×\displaystyle\frac{1}{\sqrt{2}}\)
\(n_2=\displaystyle\frac{\sqrt{6}}{2}\)
こうして、ガラスの屈折率は\(n_2=\displaystyle\frac{\sqrt{6}}{2}\)であると分かりました。参考までに、\(\displaystyle\frac{\sqrt{6}}{2}≒1.22\)です。
2) このガラス板を真上から見る場合、厚さは何cmに見えるでしょうか
光の問題を解くとき、どのように像が見えるのか理解しなければいけません。人間の脳というのは、目で認識した光について、まっすぐ進んできた光と認識します。つまり屈折によって光が曲がっていたとしても、私たちの脳は直進している光であると認識するのです。
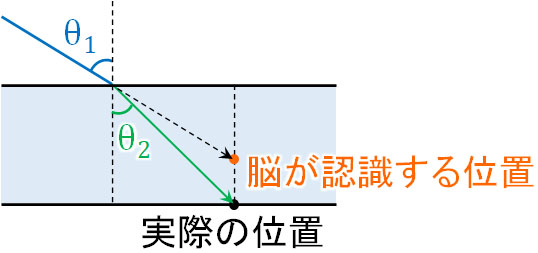
これが、屈折率の異なる媒質を通して見ると、位置が変化する理由です。そこで以下の図について、\(x\)の距離を計算すれば、私たちの脳が認識するガラスの厚さを計算できます。
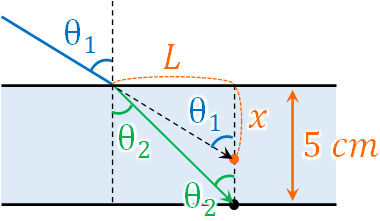
図より、\(tanθ_1=\displaystyle\frac{L}{x}\)です。また図より、\(tanθ_2=\displaystyle\frac{L}{5}\)です。そこで2つの式を利用し、\(L\)を消しましょう。
\(tanθ_2=\displaystyle\frac{L}{5}\)
\(L=5tanθ_2\)
\(tanθ_1=\displaystyle\frac{L}{x}\)へ\(L=5tanθ_2\)を代入。
\(tanθ_1=\displaystyle\frac{5tanθ_2}{x}\)
\(x=5\displaystyle\frac{tanθ_2}{tanθ_1}\)
なお真上から見るとき、角度はほぼ0になります。角度がほぼ0の場合、sinθとtanθの値はほぼ同じです。そこで問題文より、\(sinθ≒tanθ\)を利用しましょう。つまり、以下のように変形できます。
\(x=5\displaystyle\frac{sinθ_2}{sinθ_1}\)
先ほどの計算より、ガラスの絶対屈折率は\(n_2=\displaystyle\frac{\sqrt{6}}{2}\)とわかっています。また問題文より、空気中の屈折率は1なので以下の式を作れます。
\(1×sinθ_1=\displaystyle\frac{\sqrt{6}}{2}×sinθ_2\)
\(\displaystyle\frac{sinθ_2}{sinθ_1}=\displaystyle\frac{2}{\sqrt{6}}\)
\(\displaystyle\frac{sinθ_2}{sinθ_1}=\displaystyle\frac{\sqrt{6}}{3}\)
\(x=5\displaystyle\frac{sinθ_2}{sinθ_1}\)に\(\displaystyle\frac{sinθ_2}{sinθ_1}=\displaystyle\frac{\sqrt{6}}{3}\)を代入。
\(x=5\displaystyle\frac{sinθ_2}{sinθ_1}\)
\(x=\displaystyle\frac{5\sqrt{6}}{3}\)
こうして、私たちの目には\(x=\displaystyle\frac{5\sqrt{6}}{3}\)の厚さのように見えます。参考までに、\(\displaystyle\frac{5\sqrt{6}}{3}≒4.08\)です。
全反射と臨界角の計算
なお場合によっては、もう一方の媒質に光が入らないケースがあります。\(n_1>n_2\)の場合、入射角よりも屈折角のほうが大きいです。そのため入射角が大きくなると屈折角が90°になってしまい、光が一方の媒質に入らなくなるのです。この現象を全反射といいます。
なお、全反射が起こるときの入射角(下図の\(θc\)が該当)を臨界角といいます。
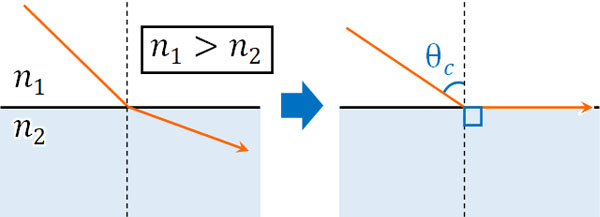
なお屈折角の法則より、速さや波長、屈折率を利用することによって臨界角を得ることができます。例えば、以下の問題の答えは何でしょうか。
- 媒質1の屈折率が2であり、媒質2の屈折率が\(\sqrt{3}\)のとき、臨界角はいくらでしょうか。
\(n_1sinθ_1=n_2sinθ_2\)より、以下のように式を作って計算しましょう。
\(n_1sinθ_1=n_2sinθ_2\)
\(2sinθ_1=\sqrt{3}sin90°\)
\(sinθ_1=\displaystyle\frac{\sqrt{3}}{2}\)
\(θ=60°\)
こうして、臨界角は60°であるとわかりました。
私たちが陸上から水中を観察するとき、遠くにある水中の物体は見えなくなります。物を見るためには、物に光が当たり、反射した光が私たちの目に入る必要があります。ただ遠くにある水中の物体では、以下のように物体からの光が水面で全反射します。
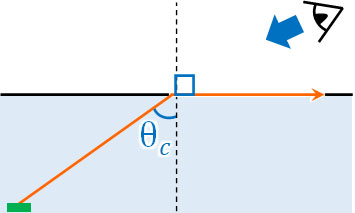
こうして、私たちの目に光は届きません。光が空気中に出れないため、私たちは物体を認識することができないのです。
光の分散:波長によって屈折率が異なる
光が屈折するとき、屈折率には波長が関与していると解説しました。これはつまり、波長によって屈折率が異なることを意味しています。
私たちが認識する光というのは、赤やオレンジ、黄、緑、青、紫など多くの色が混ざっています。多くの色が混ざる結果、白色光になります。これらの光は可視光と呼ばれ、私たちの目で認識できます。
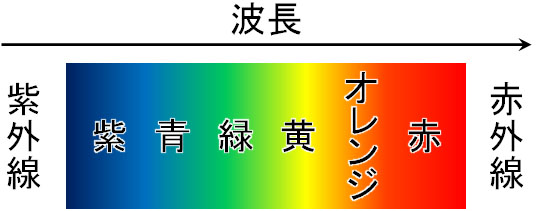
一方、赤色よりも波長が長い場合は赤外線と呼ばれ、紫色よりも波長が短い場合は紫外線と呼ばれます。赤外線や紫外線は私たちの目で色を認識することができません。
重要なのは、これらの色は波長が異なることです。赤色は波長が長く、青色や紫色は波長が短いです。結論をいうと、波長が長いと屈折しにくく、波長が短いと屈折しやすいです。つまり赤色は屈折しにくく、紫色は屈折しやすいです。
そのためプリズム(三角柱のガラス)を通すことにより、光を色ごとに分けることができます。この現象を光の分散といいます。
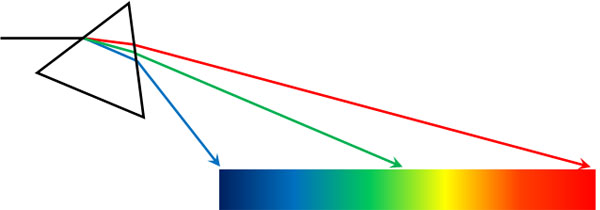
私たちは多くの場面で光の分散を認識しており、虹は光の分散によって起こります。空気中に水滴が漂い、光が水滴を通過することで光の屈折が起こった結果、光の分散が起こるのです。
光の反射と屈折の公式を利用する
異なる媒体に光が当たるとき、光は反射または屈折をします。光の反射は容易に理解できるため、光の屈折を重点的に学びましょう。
ホイヘンスの原理を学べば、光が屈折する理由がわかります。また光の屈折に関する公式では角度、光の速さ、波長、屈折率の関係が重要です。これらの関係を利用して計算問題を解くことになるため、屈折の法則で利用される公式を覚えましょう。
また場合によっては、光は全反射します。光が全反射する場合、光は異なる媒質に入ることができません。屈折の法則を利用することにより、全反射するときの臨界角を計算できます。さらに、光の分散についても学びましょう。
私たちは全員、光を目で認識しています。また光の屈折が関わる現象を目で見ています。これらの現象がなぜ起こるのか理解しましょう。






