高校数学や統計学で学ぶ分野の一つに条件付き確率があります。特定の条件が起こったとき、ある事象が起こる確率を計算するのが条件付き確率です。
特定の条件が起こるときについて、確率を計算しなければいけない場面があります。条件付き確率を理解していないと誤答することは多く、公式の意味を理解して問題を解かなければいけません。
なお公式を覚えても答えを出せるようになることはありません。そのため、条件付き確率をどのように計算すればいいのか理解しましょう。また条件付き確率の公式を利用することによって、2つのイベントが同時に起こる確率を計算することもできます。
条件付き確率というのは、統計学で重要な概念(ベイズ定理など)を理解するために必須となる知識です。そこで、ここでは条件付き確率を計算する方法を解説していきます。
もくじ
特定の条件が起こったとき、ある事象が起こる確率を計算する
確率の計算をするとき、特定の条件が起こったときについて、ある事象が起こる確率を計算しなければいけないケースは多いです。
一般的な計算では、以下の確率を求めます。
- 2枚のコインを投げ、2枚とも表が出る確率
- サイコロを2つ投げ、目の合計が10以上になる確率
- サッカーワールドカップでブラジルがベスト4に入る確率
全体の事象を計算した後、いくつの発生イベントがあるのか数えれば確率を計算することができます。
一方、条件付き確率では以下のようになります。
- コインを投げて少なくとも一枚が表の場合、2枚とも表が出る確率
- サイコロを2つ投げ、一つのサイコロの目が5の場合、目の合計が10以上になる確率
- サッカーワールドカップで日本が決勝トーナメントに参加しているとき、ブラジルがベスト4に入る確率
このように、特定の条件が加わる場合は確率が変わります。こうしたとき、条件付き確率を利用することによって計算します。
条件付き確率の公式で利用する\(P(A∩B)\)と\(P(A|B)\)の意味
条件付き確率を学ぶとき、高校数学や統計学で必ず理解しなければいけない記号が\(P(A∩B)\)と\(P(A|B)\)です。これは何を意味しているのでしょか。まずは、一般的な確率の計算方法を復習しましょう。
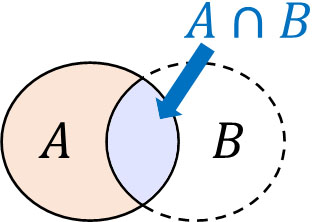
AとBの2つの事象が起こるとき、以下のように図(ベン図)を作ることができます。

AとBが両方とも起こるとき、\(A∩B\)と表します。またAとBが両方とも起こる確率については、Probability(P)を利用して \(P(A∩B)\)と表します。
\(A∩B\)がわかれば、\(P(A∩B)\)を計算することができます。例えば、以下の問題の答えは何でしょうか。
- サイコロを2つ投げ、目の合計が10以上になる確率
2つのサイコロを投げる場合、全体の場合の数は36通りです。それでは、目の和が10以上になるケースはいくらあるでしょうか。以下の場合、目の和が10以上になります。
- (5,5)
- (5,6)
- (6,5)
- (6,6)
そのためサイコロAとサイコロBを投げるとき、\(A∩B\)となるケース(目の和が10以上になるケース)は4通りです。全体のイベント36通りであるため、\(P(A∩B)\)は以下のようになります。
\(P(A∩B)=\displaystyle\frac{4}{36}=\displaystyle\frac{1}{9}\)
特定の条件が起こるときの確率を計算する
それでは次に、特定の条件が起こるときの確率を計算してみましょう。Bという条件が起こるとき、Aが起こる確率を\(P(A|B)\)と表します。例えば、以下の問題の答えは何でしょうか。
- サイコロを2つ投げ、一つのサイコロの目が5の場合、目の合計が10以上になる確率
この場合、全体の数が少なくなります。一つのサイコロの目は5であるため、もう一方のサイコロのイベントは以下の6通りです。
- (5,1)
- (5,2)
- (5,3)
- (5,4)
- (5,5)
- (5,6)
「一つのサイコロが5の目になる」という条件をBとすると、全体のイベント数は6です。この条件のとき、もう一つの条件である「目の合計が10以上になるイベント(\(A∩B\))」は(5,5)と(5,6)の2つです。
前述の通り、Bという条件が起こるとき、Aが起こる確率を\(P(A|B)\)と表します。全体のイベント数が6つであり、目の合計が10以上になるイベント(\(A∩B\))が2つであるため、「一つのサイコロの目が5の場合、目の合計が10以上になる確率\(P(A|B)\)」は以下のようになります。
\(P(A|B)=\displaystyle\frac{2}{6}=\displaystyle\frac{1}{3}\)
このように特定の条件が起こる場合の全体のイベント数をBとするとき、同時にAが起こる確率は以下のように計算できます。
- \(P(A|B)=\displaystyle\frac{A∩B}{B}\)
ただ、この公式を覚える必要はありません。考え方は一般的な確率の計算方法と同じだからです。
全体の数と発生するイベント数がわかれば、確率を計算することができます。条件付き確率では、「特定の条件下で何通りの方法があるのか(B)」「両方のイベントが起こるのは何通りあるのか(\(A∩B\))」を数えて計算すればいいです。
確率を利用して条件付き確率を計算する
このとき、\(P(B)\)はBが起こる確率を表します。また\(P(A∩B)\)は\(A∩B\)となる確率を表します。そこでBや\(A∩B\)のイベント数を利用する代わりとして、「Bが発生する確率\(P(B)\)」と「\(A∩B\)となる確率\(P(A∩B)\)」を利用して、以下の公式を作ることもできます。
- \(P(A|B)=\displaystyle\frac{P(A∩B)}{P(B)}\)
一つのサイコロを投げ、5が出る確率は\(\displaystyle\frac{1}{6}\)です。またサイコロを2つ投げる場合は36通りの方法があり、一つの目が5のときに目の和が10以上になるのは(5,5)と(5,6)の2通りです。そのため、\(P(A∩B)\)は以下のようになります。
\(P(A∩B)=\displaystyle\frac{2}{36}=\displaystyle\frac{1}{18}\)
そこで先ほどの公式を利用して、\(P(A|B)\)の確率を計算してみましょう。以下のようになります。
\(P(A|B)=\displaystyle\frac{1}{18}÷\displaystyle\frac{1}{6}=\displaystyle\frac{1}{3}\)
こうして、先ほどと同じ答えを出すことができました。「条件Bが発生する確率(またはイベント数)」と「条件Aと条件Bが同時に発生する確率(またはイベント数)」を利用することによって、条件付き確率を計算することができます。
公式を覚えたとしても、何が条件Bに当たるのかわかりません。そこで条件Bが起こるときのイベント数または確率を利用し、意味を理解したうえで計算できるようになりましょう。
なぜ条件付きを理解するのが重要なのか
それでは、なぜ条件付き確率を理解することが重要なのでしょうか。この理由として、条件付き確率を理解していないとほとんどのケースで誤答となる問題が多いからです。
例えば、以下の問題の答えは何でしょうか。
- Aさんには2人の子供がいます。子供のうち、一人は男性であるとわかっています。もう一方の性別が男性である確率はいくらでしょうか。
恐らく、あなたが出した答えは\(\displaystyle\frac{1}{2}\)ではないでしょうか。「一人の子供が男性であるため、もう一方の子供が男性でなる確率は\(\displaystyle\frac{1}{2}\)になる」と多くの人が考えます。
ただ、答えは\(\displaystyle\frac{1}{2}\)ではなく\(\displaystyle\frac{1}{3}\)です。なぜ、このような答えになるのでしょうか。先ほどのサイコロの問題と比べて何が違うのでしょうか。
二人の子供の性別について、以下の4通りの方法を考えることができます。
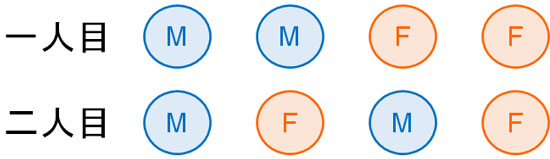
どれも等しく\(\displaystyle\frac{1}{4}\)の確率となります。また重要なのは、与えられている情報が「一人が男性である」ことです。必ずしも、最初の子供が男性であるとは限りません。二人目の子供が男性かもしれないのです。そのため、最初の子供を男性に固定してはいけません。
また、少なくとも一人の子供が男性である確率\(P(B)\)は\(\displaystyle\frac{3}{4}\)です。また両方の子供が男性である確率\(P(A∩B)\)は\(\displaystyle\frac{1}{4}\)です。そのため、一人の子供が男性のとき、もう一方が男性である確率\(P(A|B)\)は以下のようになります。
\(P(A|B)=\displaystyle\frac{1}{4}÷\displaystyle\frac{3}{4}=\displaystyle\frac{1}{3}\)
参考までに、先ほどの問題が「最初に生まれた子供が男性であるとわかっている場合、二番目に生まれた子供の性別が男性である確率は何か」であれば、答えは\(\displaystyle\frac{1}{2}\)になります。
このケースであれば、一人目の子供は男性であると固定されています。一人目と二人目のうち、どちらが男性なのかわかっていない先ほどの問題とは内容が異なります。このように前提条件によって、確率では答えが違ってきます。
公式を変形すると、確率の乗法定理になる
ここまでの内容が条件付き確率の考え方です。なお先ほど、以下の公式を利用することによって条件付き確率を計算できることを説明しました。
- \(P(A|B)=\displaystyle\frac{P(A∩B)}{P(B)}\)
そこで、この公式を変形しましょう。両辺に\(P(B)\)をかけることによって、以下の公式を作ることができます。
- \(P(A∩B)=P(A|B)×P(B)\)
これを確率の乗法定理といいます。つまり条件付き確率を利用することによって、AとBが同時に起こる確率を計算できます。この公式を覚える必要はなく、条件付き確率を理解していれば、公式を変形することによって確率の乗法定理を導き出せます。
確率の乗法定理を利用し、確率を計算する
それでは、実際に確率の乗法定理を利用して確率の計算をしてみましょう。特定の条件が起こる確率\(P(B)\)と条件付き確率\(P(A|B)\)を利用し、両方が起こる確率\(P(A∩B)\)を計算するのです。
例えば、以下の問題の答えは何でしょうか。
- 8本のうち、3本の当たりクジがあります。Aさんが一本のクジを引き、クジを戻さずに続けてBさんが引きます。AさんとBさんの両方が当たる確率はいくらでしょうか。
まず、Aさんが当たりクジを引く確率\(P(B)\)は\(\displaystyle\frac{3}{8}\)です。
またAさんが当たりクジを引いた後、7本のうち2本が当たりクジです。そのため、この状況でBさんが当たりクジを引く確率\(P(A|B)\)は\(\displaystyle\frac{2}{7}\)です。そのため、AさんとBさんの両方が当たりクジを引く確率は以下のように計算できます。
\(P(A∩B)=\displaystyle\frac{3}{8}×\displaystyle\frac{2}{7}=\displaystyle\frac{3}{28}\)
こうして、2つの条件を同時に満たす確率を計算できます。条件付き確率の計算方法を理解していれば、確率の乗法定理を利用することによって答えを出すことができます。
特定の条件下で起こる確率を計算する
確率の計算をするとき、条件付き確率は少し概念が難しいです。まず、「条件付き確率の計算をしなければいけない」と気づくのが難しいケースが多いです。この例として、「子供二人のうち、少なくとも一人が男性であるとわかっているケース」を解説しました。
そこで問題文を注意深く読み、条件付き確率を求めなければいけないことを見抜きましょう。特定の事象が起こるイベント数や確率を計算し、答えを得るようにします。公式を覚えても計算は難しいため、条件付き確率を計算するときの考え方を理解しましょう。
また条件付き確率を計算できるようになれば、公式を変形することによって確率の乗法定理を利用できるようになります。2つの条件を同時に満たす確率を計算したいとき、確率の乗法定理を活用しましょう。
条件付き確率は統計学を理解するときに重要な知識です。そこで統計学の基本として、条件付き確率の計算を行えるようにしましょう。