統計で必要なサンプルサイズ（サンプル数）の決め方・計算方法

データを集めたあと、統計処理することによって集めたサンプルデータに有意差があるかどうかを確認することは重要です。ただデータを集める前に、実験計画を立てなければいけません。

このとき、多くの人が疑問に思うこととして「どのようにしてサンプルサイズ（サンプル数）を決めればいいのか」があります。必要なサンプルサイズがわかれば、実験計画を立てやすくなります。

必要なサンプルサイズは公式を利用することによって得ることができます。ただ実際のところ、どれくらいのサンプルを集めればいいのか不明なケースは多く、その場合は他の人の手順を真似させてもらえば問題ありません。

統計データを集めるとき、多くの人が必要なサンプルサイズに悩みます。そこで、どのように考えて集めるデータ数を決めればいいのか解説していきます。

1 統計学でのサンプル数とサンプルサイズの違い
2 95%信頼区間を得る公式を利用し、サンプルサイズを逆算する
- 2.1 標準偏差と誤差の許容度を利用し、サンプルサイズを計算する
3 多くの場合、必要なサンプルサイズはわからない
- 3.1 類似論文や研究方法を検索し、サンプルサイズを確認する
- 3.2 少数のサンプルサイズでも問題ないケース：t検定の利用
4 研究で必要なデータ数を理解する

統計学でのサンプル数とサンプルサイズの違い

まず、統計学ではサンプル数とサンプルサイズで言葉の意味が異なります。実際のところ、両者を使い分ける意味はほとんどありません。ただ、厳密には以下のような違いがあります。

サンプル数：群の数
サンプルサイズ：データ数

例えば母集団から100個のデータを取り出す場合、サンプルサイズは100です。また、サンプルサイズ100のデータを3回取るとき、サンプル数は3です。

ただ「データ数＝サンプル数＝サンプルサイズ」という前提の教科書は多いですし、言葉の定義を厳密に考える意味はありません。それよりも、わかりやすさのほうが重要です。また、当サイトでも「データ数＝サンプル数」と考えて記述している個所はたくさんあります。

そうはいっても、サンプル数とサンプルサイズでこうした意味の違いがあることは事前に理解しておきましょう。

95%信頼区間を得る公式を利用し、サンプルサイズを逆算する

それでは、どのようにしてサンプルサイズを推測すればいいのでしょうか。このとき必要なデータ数というのは、公式から得ることができます。

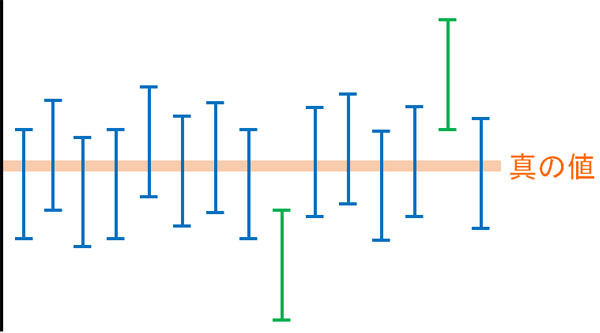
統計処理をするとき、多くのケースで95%信頼区間（または99%信頼区間）を利用します。「100回測定するとき、95回はその間に真の値を含むであろう」と推測できる区間が95%信頼区間です。

このとき、標本の標準誤差SEは以下の公式によって得られることを既に学んでいると思います。

\(SE=\displaystyle\frac{σ}{\sqrt{n}}\)

また95%信頼区間を得る場合、標準誤差に対して1.96倍することで範囲を出します（99%信頼区間の場合は2.58倍する）。そのため誤差範囲は以下のようになります。

誤差範囲＝\(1.96×\displaystyle\frac{σ}{\sqrt{n}}\)

つまり標準偏差\(σ\)がわかっている場合、許容できる誤差範囲を設定することによって、必要なサンプルサイズがわかります。

標準偏差については、既にわかっている標本データを利用しましょう。また許容できる誤差範囲については、あなたが決めることができます。例えば誤差範囲を2%とする場合、0.02を誤差範囲に代入しましょう。こうして、逆算によって計算します。

標準偏差と誤差の許容度を利用し、サンプルサイズを計算する

それでは、実際に必要なサンプルサイズを計算してみましょう。以下の問題に答えましょう。

平均寿命が1000時間の製品についてランダムに抽出し、規格に適合しているかどうかを調べます。製品の寿命は正規分布しており、標準偏差\(σ\)は200です。また、誤差の寿命を40時間にしたいです。95%信頼区間を利用する場合、必要なサンプルサイズはいくらでしょうか。

標準偏差\(σ\)は200であり、許容できる誤差範囲は40時間です。そこで、以下の計算をしましょう。

\(40=1.96×\displaystyle\frac{200}{\sqrt{n}}\)

\(\sqrt{n}=1.96×\displaystyle\frac{200}{40}\)

\(\sqrt{n}=9.8\)

\(n=96.04\)

つまり、96個のデータ数であれば十分であるとわかります。標本標準偏差（標準誤差）がわかっている場合、この方法によって必要なデータ数を計算しましょう。

多くの場合、必要なサンプルサイズはわからない

ただ実際のところ、多くの実験では母集団の平均値や分散、標準偏差が不明である場合が多いです。また初めて行う実験であれば、そもそも標本データが存在しません。標本標準偏差が事前にわからないため、必要なサンプルサイズを知ることができないケースは多いです。

なお、統計学で有名な検定法にt検定があります。母平均がわからない場合、t検定を利用します。多くの研究でt検定が利用されるのは、母集団が未知だからです。t検定が統計学で最もひんぱんに利用されることからわかる通り、実験前は標準偏差がわからないことが多いです。

それでは標準偏差がわからない場合、どのようにして必要なデータ数を知ればいいのでしょうか。勘によって必要なデータ数を決めてもいいのでしょうか。

新たにデータを集める場合、母集団はわかりませんし、当然ながら標本データは存在しません。その場合、以下の方法でサンプルサイズを決めましょう。

類似論文や研究方法を検索する
少数サンプルで問題ない場合、1つの群につき6～10のデータを集める

それぞれの方法について解説していきます。

類似論文や研究方法を検索し、サンプルサイズを確認する

最も一般的であり、確実な方法は「ほかの人がしているデータの集め方を真似する」ことです。つまり、類似論文や研究方法がどのように行われているのか検索・調査するのです。

例えば政党の支持率について調査するとき、ほかのマスメディアの多くが2000～3000人を対象に調査している場合、同じように2000～3000人に対してアンケートを取得するべきです。アンケート人数が100人だと少ないですし、1万人だと無駄にコストが高くなります。

他には毒性試験をするとき、類似論文で1つの群につき8つのデータを取得している場合、同じように1つの群につき少数のサンプルで問題ありません。

母集団がわからない以上、ヒントなしに必要なサンプルサイズを推測するのは不可能です。そこでほかの人がどのようにデータを集めているのか調査しましょう。類似論文やほかの人の研究方法を真似することは、必要なサンプルサイズを知る最も効果的な方法の一つです。

少数のサンプルサイズでも問題ないケース：t検定の利用

なお多くのケースでは、必要なデータ数は少数で問題ないことがよくあります。例えば新製品のテストをするとき、何百個も製品を用意して耐久テストをするのはコストが大きいです。また動物実験をする場合、何百匹もの動物を利用してテストするのは大変です。

実際のところ、1つの群につき6～10のデータ数があれば統計処理することが可能です。少数サンプルのときに利用する検定法はt検定であり、t検定というのは、「少ないサンプル数であっても、有意差があるかどうかを判断できるツール」として開発されています。そのためサンプルサイズが多くなくてもt検定によって有意差を判断できるのです。

もちろん、サンプル数は多いほど優れています。また新薬の臨床試験のように、何万ものデータ数が必要になる研究もあります。

ただ多くの場合、類似論文やほかの人の研究手法を確認すると、少数のサンプル数で問題ないケースは多いです。この場合、1つの群につき6～10のデータ数になれば十分というわけです。