統計学で重要な概念がカイ二乗分布(χ2分布)です。母分布の分散がわからないとき、カイ二乗分布を利用することによって母分散を推定することができます。
それでは、カイ二乗分布は正規分布とは何が違うのでしょうか。また、どのようにして母分散の推定をするのでしょうか。
カイ二乗分布では公式を利用して計算することになります。内容は難しくなく、中学数学を利用することによってカイ二乗分布を理解できます。標準正規分布を事前に理解している必要はあるものの、正規分布を学んでいれば問題なくカイ二乗分布がわかります。
統計学を学ぶとき、すべての人で理解しなければいけないのがカイ二乗分布です。そこでカイ二乗分布とは何かについて、正規分布との関係や自由度を用いた母分散の推定を解説していきます。
もくじ
理論値とのズレをカイ二乗分布で調べることができる
統計学で必ず学ぶのがカイ二乗分布です。多くの場合、先にt分布を学び、そのあとにカイ二乗分布を学びます。ただ優れている教科書では、t分布よりも先にカイ二乗分布を学ぶことになります。理由は単純であり、t分布の公式はカイ二乗分布の公式を利用して出すからです。
つまりカイ二乗分布を理解していない場合、t分布を理解することはできません。そのため正規分布や区間推定(95%信頼区間)を学んだあと、t分布よりも先にカイ二乗分布を学ばなければいけません。
それでは、カイ二乗分布とは何なのでしょうか。ザックリ考えると、カイ二乗分布とは「理論値とのズレを表す指標」と考えましょう。
期待値(平均値)を確認するだけでは、理論値とのズレを正確に把握することができません。例えばサイコロを投げるとき、期待値(平均)は3.5です。何度もサイコロを投げるとき、平均すると3.5に収束するのです。
サイコロには1~6の数字があり、確率はそれぞれ\(\displaystyle\frac{1}{6}\)なので、以下のように期待値を計算できます。
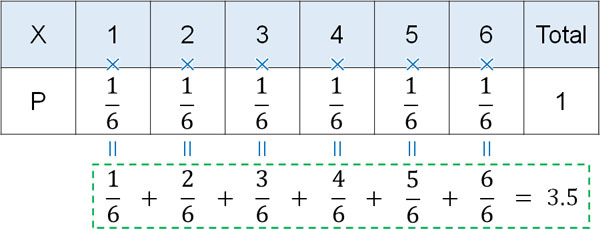
それでは、サイコロを20回投げて「1の目が10回、6の目が10回」という結果になった場合はどうでしょうか。
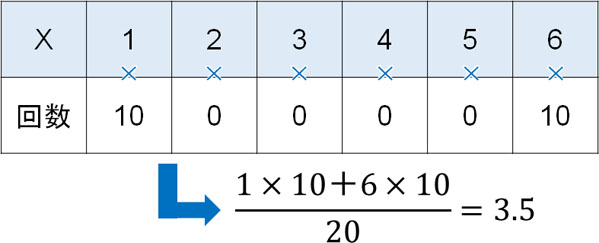
この場合についても平均値は3.5であり、サイコロを投げるときの期待値と一致します。ただ、実際にこのような結果になることは非常に珍しく、何かサイコロに細工があると考えるのが普通です。
ただ期待値を確認すると何も問題がないため、期待値のみを利用する場合であれば、本当にデータが正しいのかどうか判断することができません。そこで理論値とのズレを確認するため、期待値とは別の指標が必要になります。そこでカイ二乗分布を利用するのです。
母分散の区間推定を行う:カイ二乗分布(χ2分布)は確率分布
カイ二乗分布(χ2分布)によって何がわかるかというと、母分散の推定をすることができます。母集団を集めるのは現実的ではなく、標本として小数のサンプルを利用して統計処理することがよくあります。
このとき、母分散の区間推定をするときにカイ二乗分布が利用されます。つまり特定の値を推測するのではなく、「この間に母分散が存在するのではないか」という推定をするときにカイ二乗分布が役立ちます。
母分散の推定をするためには、必ず標本を利用します。標本分散というのは、カイ二乗分布します。つまり標本を利用することによって、母分散の区間推定が可能というわけです。
標本を利用することによって母分散の区間推定をするためのツールがカイ二乗分布(χ2分布)と理解しましょう。
カイ二乗値の計算:標準正規分布での確率変数を二乗する
カイ二乗分布は確率分布です。また、カイ二乗値を計算することによって母分散の推定を行えるようになります。そこで、最初にカイ二乗値とは何かを理解しましょう。
カイ二乗分布を学ぶとき、必ず標準正規分布を理解していないといけません。そのため、標本標準偏差を理解しているという前提で話を進めていきます。
標本標準偏差では、すべてのデータについて横幅が同じです。標準偏差を利用して、横幅±1の範囲に全データの68.3%が含まれるようになります。また±2の範囲には、全データの95.5%が含まれます。
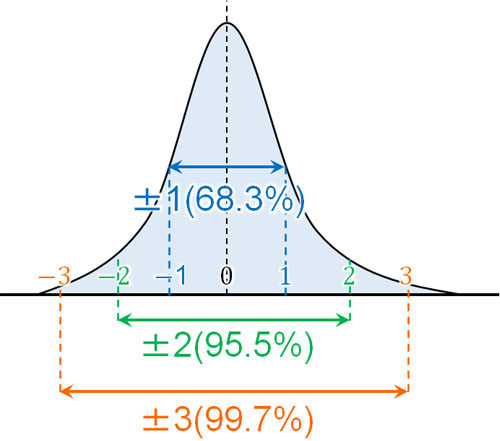
そこで標本の観測データについて、「標準正規分布の確率変数」を二乗しましょう。その後、値をすべて足すとカイ二乗値Vになります。例えば標準正規分布での観測データ(確率変数)がそれぞれZ1、Z2、Z3の場合、カイ二乗値Vは以下のようになります。
\(V=(Z_1)^2+(Z_2)^2+(Z_3)^2\)
具体的にカイ二乗値を計算してみましょう。標準正規分布の確率変数に直すとき、以下の公式を利用します。
- \(Z=\displaystyle\frac{X-μ}{σ}\)
そこで、以下の問題を解いてみましょう。
- 観測データが「X1=2、X2=5、X3=-1」の標本について、母平均が2のとき、カイ二乗値を計算しましょう。
平均値は2であり、分散は以下のように計算できます。
\(\displaystyle\frac{0^2+3^2+(-3)^2}{3}=6\)
また、標準偏差は\(\sqrt{6}≒2.45\)です。平均値\(μ\)が2、標準偏差\(σ\)が2.45のため、標準正規分布での確率変数はそれぞれ以下のようになります。
\(Z_1=\displaystyle\frac{2-2}{2.45}=0\)
\(Z_2=\displaystyle\frac{5-2}{2.45}≒1.22\)
\(Z_3=\displaystyle\frac{-1-2}{2.45}≒-1.22\)
こうして標準正規分布での確率変数に変換するとき、Z1の確率変数は0、Z2の確率変数は1.22、Z3の確率変数は-1.22になることがわかります。そこで、3つの確率変数を二乗して足しましょう。
\(V=0^2+1.22^2+(-1.22)^2≒2.98\)
こうして標準正規分布で利用する確率変数をすべて二乗し、足すことによってカイ二乗値Vを得ることができました。
サンプルによって正規分布の横幅は異なります。ただ標準正規分布に直す場合、すべてのデータについて横幅が同じになります。そのため標準正規分布の確率変数を利用すれば、標本データの値に関係なく利用可能なデータを得ることができるのです。
いずれにしても、カイ二乗分布を利用するためには、「標準正規分布の確率変数をすべて二乗し、足せばいい」ことを理解すればいいです。
自由度3でのカイ二乗分布を確認する
次に自由度3のカイ二乗分布を確認しましょう。自由度というのは、要はサンプル数のことです。先ほどは3つのサンプル(X1=2、X2=5、X3=-1)を利用したため、自由度3でカイ二乗分布を考えてみましょう。
得られるサンプルについて、データが異なれば標準正規分布の確率変数(値)は変わります。平均値に近いデータを得られる場合、標準正規分布の確率変数はどれも小さくなります。一方で平均値から逸脱したデータが多い場合、標準正規分布の確率変数は値が大きくなります。
このときサンプル数が3(自由度3)のカイ二乗分布は以下のような確率分布になります。

サンプルを3つ集めてカイ二乗値Vを計算する場合、\(V=2\)になる確率が最も高く、Vの値が大きくなる(または小さくなる)にしたがって確率は低くなります。そのため、正規分布とは形が異なるとわかります。ひとまず、自由度3のカイ二乗分布はこのような形になると理解すれば問題ありません。
自由度\(n\)で異なるグラフの形
カイ二乗分布は自由度(集めるデータ数)によってグラフの形が変わります。自由度が少ない場合、急勾配のあるグラフになります。一方でサンプル数が多くなると、正規分布に近い形となります。
以下が自由度\(n\)とカイ二乗分布の形です。
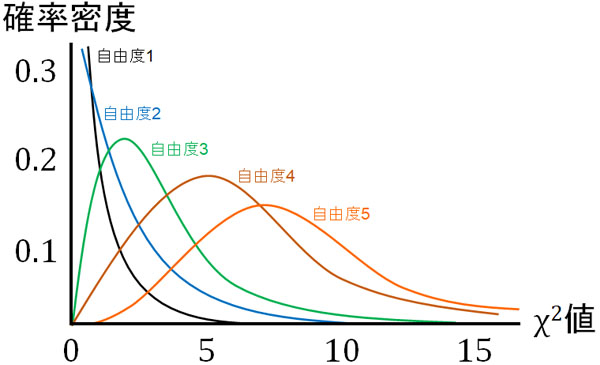
それでは、このグラフは何を意味しているのでしょうか。また自由度1のとき、なぜ急勾配のグラフになるのでしょうか。自由度が大きくなると、なぜ正規分布に近くなるのでしょうか。
・自由度1のケース
まず自由度1の場面を考えてみましょう。母集団から一つのサンプルを取り出す場合(自由度1)、どのようなデータを得られるでしょうか。
母集団が正規分布する場合、当然ながら平均(期待値)に近い値を得られやすいです。また前述の通り、標準正規分布で横幅が-1~1の間に68.3%のデータがあります。要は自由度1の場合、一つのサンプルを取り出すことになるため、平均に近い値(0に近い確率変数)を得られやすいです。
要は、確率変数が0に近い確率が非常に高いため、当然ながら自由度1のカイ二乗分布では0に近いほど得られる確率が高くなります。
・自由度3のケース
一方で母集団から3つのサンプルを取り出す場面を考えてみましょう(自由度3)。この場合、平均に近い値が含まれやすいものの、期待値とは離れた値を得られることもあります。
標準正規分布での確率変数について、前述の通り-1~1の間に含まれる確率は68.3%です。カイ二乗値を計算するとき、値を二乗するため、68.3%の確率で二乗の値が0~1となります。ただ3つのサンプルを取り出せば、そのうち1つくらいは二乗の値が1以上になるのは普通です。
一方、95.5%の確率で確率変数は-2~2の間になります。言い換えると、95.5%の確率で二乗の値が0~4の間に存在することになります。稀にしか起こらないものの、二乗の値が3や4などになることもあるのです。
このように考えると、ランダムに取り出した3つのサンプルについて、標準正規分布での確率変数を求めた後に二乗し、足す場合に「カイ二乗値がほぼ0になる」という確率は低いとわかります。一方でカイ二乗値が5や6のように大きくなる確率も低いです。
そのため自由度3の場合、カイ二乗値が1~3になる確率が高いというわけです。そのため、先ほど記した図のようなグラフになります。
・自由度が大きい場合
サンプル数が多く、自由度が大きい場合、それに伴って標準正規分布での確率変数はさまざまな値を取るようになります。また、こうした値を合計すると正規分布するようになります。この性質については、中心極限定理で既に学んでいると思います。
サンプルを取り出すとき、平均値に近い値を得られる確率が高いです。そのため自由度1の場合、急勾配をもつグラフを描きます。ただ多くのサンプルを取り出す場合、平均値から逸脱する値を多く含むことになります。そのためこうした値を考慮すると、正規分布と同じ形になるというわけです。
カイ二乗分布と自由度のグラフを見るとき、多くの人が意味を理解できないと思います。そこで、カイ二乗分布のグラフが何を意味しているのか学びましょう。
標準正規分布の確率変数を二乗し、すべて足し算することでカイ二乗値を得られます。これを理解すれば、なぜ自由度の変化によってカイ二乗分布のグラフの形が変わるのか理解できるはずです。
母分散をカイ二乗分布で推定する手順
カイ二乗分布というのは、理論値からのズレを知るときに役に立ちます。標準正規分布を利用することによって、すべてのデータについて「自由度3の場合、理論的にはカイ二乗値が1~3の周辺にあるべき」となります。自由度によって理論値は異なるものの、自由度ごとに理論的なカイ二乗値が存在するのです。
例えばサイコロを20回投げ、「1の目が10回、6の目が10回という結果」はどうでしょうか。この場合は期待値3.5に対して、1という小さい値(または6という大きい値)を何度も得ることになります。期待値との距離が大きいため、標準正規分布での確率変数は大きくなります。
こうして期待値は3.5であるものの、カイ二乗値が異常に大きくなってしまい、「理論的な値よりも大きくずれている」ことを客観的に説明できます。カイ二乗分布が理論値とのズレで役に立つというのは、こうした理由があるのです。
また重要なのは、カイ二乗分布を利用して母分散の区間推定が可能なことです。どのように計算するかというと、カイ二乗分布の95%区間を利用します。カイ二乗分布について、自由度ごとに「95%のデータが存在する区間」が既に決まっています。
カイ二乗分布について、自由度と相対度数の関係は以下のようになっています。
| 自由度 | 相対度数97.5% | 相対度数2.5% |
| 1 | 0.001 | 5.023 |
| 2 | 0.051 | 7.377 |
| 3 | 0.216 | 9.348 |
| 4 | 0.484 | 11.143 |
| 5 | 0.831 | 12.833 |
| 6 | 1.237 | 14.449 |
| 7 | 1.690 | 16.013 |
例えば自由度3の場合、カイ二乗値Vが0.216以上の部分に97.5%のデータが含まれます。またカイ二乗値Vが9.348以上の部分に2.5%が含まれます。
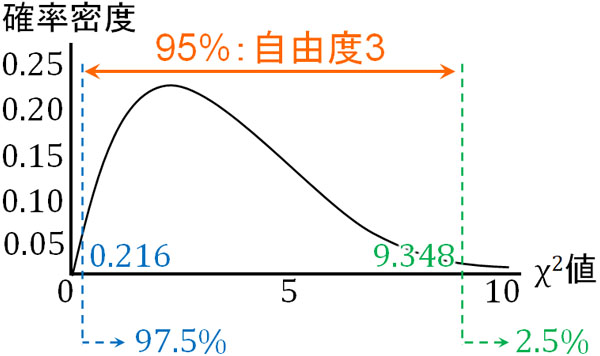
両側に2.5%があるため、自由度3のカイ二乗分布では、サンプルを取り出すときに95%の確率で0.216≦V≦9.348の範囲に収まります。
カイ二乗分布を利用することによって、95%の確率で予言することができます。これは自由度とカイ二乗値(χ2値)がわかれば可能です。
なお当然ながら、95%の間に収まるデータだけでなく、99%の確率でデータが収まる確率密度の表も存在します。これについては95%信頼区間を利用して計算したいのか、それとも99%信頼区間を利用して計算したいのかによって利用する値が異なります。
母平均を利用し、母分散と母標準偏差を推定する
それでは、実際に母平均を利用して母分散と母標準偏差を推定してみましょう。母集団について、母平均を\(μ\)、母標準偏差を\(σ\)とします。母集団から3つのサンプルを取り出すとき、標本としてX1、X2、X3を観測しました。
それぞれのデータを標準正規分布の確率変数に直し、二乗と足し算をすることでカイ二乗値(χ2値)を得られます。そのため、以下のような計算になります。
\(V=\left(\displaystyle\frac{X_1-μ}{σ}\right)^2\)\(+\left(\displaystyle\frac{X_2-μ}{σ}\right)^2\)\(+\left(\displaystyle\frac{X_3-μ}{σ}\right)^2\)
これまで説明した計算方法であるため、これについては問題なく理解できると思います。それでは、母平均\(μ\)が10とわかっているとき、「8、7、12」の観測データについて、母分散\(σ^2\)の95%信頼区間はいくらでしょか。
以下のように計算をしましょう。
\(V=\left(\displaystyle\frac{8-10}{σ}\right)^2\)\(+\left(\displaystyle\frac{7-10}{σ}\right)^2\)\(+\left(\displaystyle\frac{12-10}{σ}\right)^2\)
\(=\displaystyle\frac{4}{σ^2}+\displaystyle\frac{9}{σ^2}+\displaystyle\frac{4}{σ^2}\)
\(=\displaystyle\frac{17}{σ^2}\)
それではサンプル数が3(自由度3)のとき、95%の確率でカイ二乗値Vが収まる範囲はいくらでしょうか。先ほど解説した通り、自由度3では0.216≦V≦9.348の場合、サンプルは95%の間に収まります。つまり\(V=\displaystyle\frac{17}{σ^2}\)を代入すれば、母分散\(σ^2\)の95%信頼区間を得られます。
\(0.216≦\displaystyle\frac{17}{σ^2}≦9.348\)
これを満たす母分散\(σ^2\)を求めましょう。以下のようになります。

こうして、母分散の95%信頼区間は\(1.82≦σ^2≦78.7\)であるとわかります。また母標準偏差\(σ\)であれば以下のようになります。
\(\sqrt{1.82}≦σ≦\sqrt{78.7}\)
\(1.35≦σ≦8.87\)
こうして、母標準偏差の区間推定を行うことができます。95%のデータが収まるカイ二乗値は既に知られているため、数字を当てはめることによって母分散(母標準偏差)を計算することができるのです。
標本分散を利用し、自由度\(n-1\)に従う統計量Wを得る
ただ先ほどの計算は「母平均がわかっている」という、通常ではあり得ない状況で説明しました。母集団が不明であり、母平均がわかっていないため、私たちは標本として小数のサンプルを集めているわけです。それでは、母平均がわかっていない場合はどのようにして母分散(母標準偏差)を推定すればいいのでしょうか。
この場合、母平均\(μ\)の代わりとして標本平均\(\overline{X}\)を利用しましょう。標本平均は母平均とは異なるものの、母平均がわからない以上、標本平均を代用しても問題ないのです。
そこで母集団のカイ二乗値Vの代わりとして、標本のカイ二乗値Wを利用しましょう。サンプル数が3つの場合、統計量(標本のカイ二乗値)Wは以下の式になります。
\(W=\left(\displaystyle\frac{X_1-\overline{X}}{σ}\right)^2\)\(+\left(\displaystyle\frac{X_2-\overline{X}}{σ}\right)^2\)\(+\left(\displaystyle\frac{X_3-\overline{X}}{σ}\right)^2\)
母平均が標本平均に置き換わっただけなので、この式については問題ない理解できるはずです。
それでは、この式をもう少し変形してみましょう。標本の分散\(s^2\)を計算する場合、サンプルが3つの場合は以下のようになります。
\(s^2=\displaystyle\frac{(X_1-\overline{X})^2+(X_2-\overline{X})^2+(X_3-\overline{X})^2}{n}\)
※本来、標本分散では\(n-1\)になりますが、わかりやすくするため\(n\)にしています。
このとき統計量Wと標本分散\(s^2\)を比べると、分子が同じであることに気が付きます。そのため、以下の式を作ることができます。
\(W×σ^2=s^2×n\)
\(W=\displaystyle\frac{s^2×n}{σ^2}\)
このように、標本分散とサンプル数、母分散(母標準偏差)を利用することによって統計量Wを得る式を作ることができました。
重要なのは、「標本を利用する統計量Wについて、自由度\(n-1\)のカイ二乗分布に従う」ということです。つまり標本を利用する場合、カイ二乗分布で「95%のデータが入ると予想される区間」を利用するとき、自由度を一つ減らすようにしましょう。
標本を利用するときに自由度が一つ減るのかについて、理由を考えてはいけません。数学者が複雑な計算をして答えを出してくれているため、この結果をありがたく使わせてもらいましょう。私たちの目的は複雑な数学の計算ができることではなく、あくまでも統計処理できることが重要だからです。
いずれにしても標本分散とサンプル数、統計量Wを利用することによって母分散(母標準偏差)の推定が可能になります。
母平均なしに母分散の推定を行う
それでは、実際に母平均なしに母分散の推定をしてみましょう。以下のサンプルについて、母分散の95%信頼区間はいくらでしょうか。
- 8、7、12
まず、標本平均\(\overline{X}\)は9です。
\(\displaystyle\frac{8+7+12}{3}=9\)
また分散\(s^2\)は4.67です。
\(\displaystyle\frac{(-1)^2+(-2)^2+3^2}{3}≒4.67\)
そのため、統計量Wは以下のようになります。
\(W=\displaystyle\frac{4.67×3}{σ^2}=\displaystyle\frac{14.01}{σ^2}\)
サンプル数は3であるため、自由度\((3-1=)2\)のカイ二乗分布に従います。自由度2の場合、95%に収まる統計量Wはカイ二乗分布の表より以下のようになります。
\(0.051≦W≦7.377\)
そこで、\(W=\displaystyle\frac{14.01}{σ^2}\)を代入しましょう。
\(0.051≦\displaystyle\frac{14.01}{σ^2}≦7.377\)
この式を解くと以下のようになります。

こうして、\(1.9≦σ^2≦274.71\)が母分散の95%信頼区間であると計算できます。また標準偏差を求めたい場合、以下のようになります。
\(\sqrt{1.9}≦σ≦\sqrt{274.71}\)
\(1.38≦σ≦16.57\)
こうして、母標準偏差を推定することができました。このような手順によってカイ二乗分布を利用し、母分散や母標準偏差の予想値を計算できます。
カイ二乗分布の理解は統計学で重要
すべての人が統計学でカイ二乗分布(χ2分布)を学びます。ただ、「なぜ自由度が異なることでグラフの形が変わるのか」「カイ二乗分布が何を意味しているのか」を多くの人で理解できていません。そこで、カイ二乗分布とは何かを含めて学びましょう。
カイ二乗分布は確率分布であり、自由度ごとに95%信頼区間(または99%信頼区間)が既に決まっています。そのため標本平均や標本分散を利用することによって、95%信頼区間(または99%信頼区間)での母分散や母標準偏差を推定しましょう。
カイ二乗分布を利用すれば、理論値とのズレを把握できます。標本平均と期待値(母平均)とのズレがほとんどなかったとしても、理論値とのズレが大きい場合、イカサマなどの異常を疑うことができます。
カイ二乗分布は統計処理の基本です。ここまで述べたことを把握し、母分散の推定を行えるようになりましょう。また、t分布を学ぶ前に必ずカイ二乗分布を理解しましょう。