データをグラフにするとき、散布図を利用することがあります。データを点で記すことによって、散布図上のどの位置にデータがあるのか記すのです。
散布図を利用すれば、2つの要素の相関がわかります。2つの要素にどれだけ関係性があるのかを表す指標が相関です。また、どれだけ相関しているのかを示す指標として共分散と相関係数が利用されます。
ただ相関関係があっても、必ず2つの要素に因果関係があるわけではありません。統計データを読み解くとき、疑似相関があることを理解しましょう。つまり統計データを処理するとき、なぜ疑似相関が頻繁に表れるのか理解しなければいけません。
データの読み方を学べば、データが何を意味しているのか理解できるようになります。そこで、散布図や共分散、相関係数、疑似相関について解説していきます。
もくじ
散布図と相関関係を理解する
多くの場合、統計データでは度数分布表やヒストグラムを利用します。ただヒストグラムでは、複数のデータが重なって表示されるため、一つのデータがどのように分布しているのか判断できません。そこで、散布図を利用します。
散布図では点(ドット)を利用して一つのデータを表します。そのためデータが重なることなく、すべてのデータをグラフ上に描くことができます。例えば身長と体重を測定するとき、以下のようなデータを得られます。
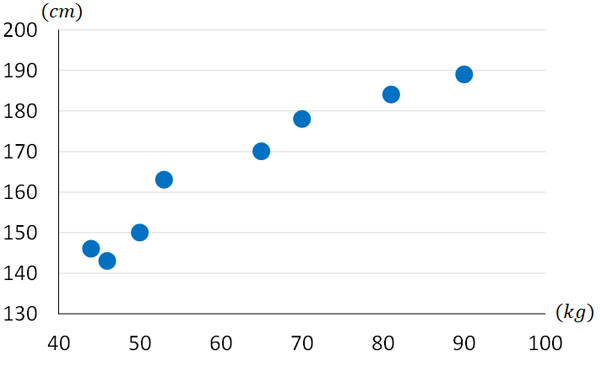
このように点で記すのが散布図です。
このグラフでは、体重が重くなるほど身長が高くなっているとわかります。散布図にすることによって、2つの要素が関係しているかどうか予測できるのです。
相関の様子:正の相関、負の相関、相関関係なし
2つの要素に関係性がある場合、データに相関があるといいます。散布図を作るとき、相関は大きく以下の3つに分かれます。
- 正の相関
- 負の相関
- 相関関係なし
正の相関というのは、データが右上がりの散布図を指します。先ほど、身長と体重のグラフを載せました。このグラフの場合、正の相関があるといえます。
一方で負の相関では、データは右下がりの散布図になります。例えば週の運動時間と体重を比較すると、運動時間が多い人ほど体重が少ないと予想できます。この場合、データは右下がりとなります(運動時間が長いほど、体重の値は低い)。こうしたデータは負の相関があるといえます。
なお中には、データがグラフ上のさまざまな場所に点在しており、右上がりでも右下がりでもないケースがあります。この場合、相関関係なしです。
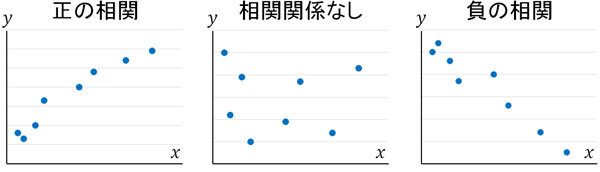
このように相関関係には、主に3つの種類があります。
共分散を利用し、正の相関と負の相関を区別する
それでは、どのように相関関係を調べればいいのでしょうか。相関関係を示す指標として共分散があります。以下が共分散を計算する公式です。
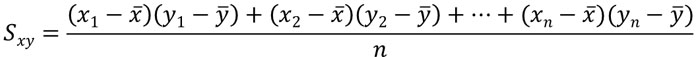
- Sxy:共分散
- \(x_1\)や\(x_2\)など:それぞれのデータの値
- \(\overline{x},\overline{y}\):\(x\)や\(y\)の平均値
- n:データの数
この公式を見ても理解できません。そこで、共分散が何を意味しているのか理解しましょう。まず、以下は何を意味しているのでしょうか。
- \((x_1-\overline{x})(y_1-\overline{y})\)
\(\overline{x}\)は\(x\)の平均値です。また、\((x_1-\overline{x})\)は\(x\)軸について、一つのデータと平均値との距離を表しています。また\(\overline{y}\)は\(y\)の平均値であり、\((y_1-\overline{y})\)は\(y\)軸について、一つのデータと平均値との距離を表しています。
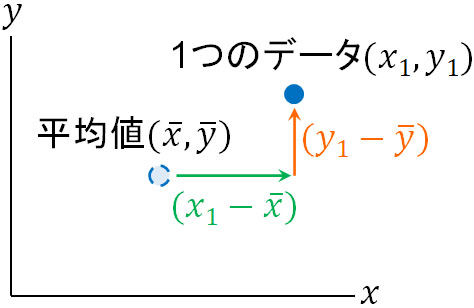
そのため\((x_1-\overline{x})(y_1-\overline{y})\)とは、\(x_1\)と\(y_1\)の偏差(データのばらつき)の積を意味しています。一つのデータについて、\(x\)と\(y\)のばらつきを掛け算しているのです。そこで一つではなく、すべてのデータについて\(x\)と\(y\)の偏差を出し、かけ算をした後に平均値を出しましょう。そうすると、先ほど記した公式になります。
つまり共分散(Sxy)というのは、一つのデータごとに偏差(ばらつき)をだしたあと、平均化した値です。
- 共分散(Sxy)=「\(x\)の偏差と\(y\)の偏差の積」の平均値
正の相関と負の相関を比べると、共分散の符号が異なります。
・正の相関の場合
正の相関を示すグラフの場合、共分散はどのようになるでしょうか。平均値よりも右上に点がある場合、\(x\)軸の偏差\((x_1-\overline{x})\)はプラスになります。また、\(y\)軸の偏差\((y_1-\overline{y})\)もプラスになります。プラスとプラスをかけると、答えはプラスになります。
次に、平均値よりも左下に点がある場合を考えましょう。この場合、\(x\)軸の偏差\((x_1-\overline{x})\)はマイナスになります。また、\(y\)軸の偏差\((y_1-\overline{y})\)もマイナスになります。マイナスとマイナスをかけると、答えはプラスになります。
つまり正の相関のあるグラフでは、\((x_1-\overline{x})(y_1-\overline{y})\)はプラスになります。そのため、共分散(Sxy)の値はプラスになります。
・負の相関の場合
一方で負の相関ではどうでしょうか。平均値の座標よりも右下にあるデータでは、\(x\)軸の偏差\((x_1-\overline{x})\)はプラスになります。一方、\(y\)軸の偏差はマイナスになります。プラスとマイナスをかけると、答えはマイナスになります。
また平均値の座標よりも左上にあるデータでは、\(x\)軸の偏差\((x_1-\overline{x})\)はマイナスになります。一方、\(y\)軸の偏差\((y_1-\overline{y})\)はプラスになります。マイナスとプラスをかけると、答えはマイナスになります。
そのため負の相関がある場合、\((x_1-\overline{x})(y_1-\overline{y})\)はマイナスになります。つまり、共分散(Sxy)の値はマイナスになります。
・相関関係がない場合
それでは、相関関係がない場合はどのようになるのでしょうか。相関関係がない場合、平均値の座標に対して、データはバラバラに位置しています。そのため\((x_1-\overline{x})(y_1-\overline{y})\)がプラスの値であることがあれば、マイナスの値であることもあります。
そのため相関関係がない場合、\(x\)の偏差と\(y\)の偏差をかけ算した後、すべて足すと値はほぼ0になります。つまり相関関係がないデータでは、共分散はほぼ0です。
- Sxy≒0
つまり、相関関係と共分散は以下の関係になっています。
- 正の相関:Sxy\(>0\)
- 相関関係なし:Sxy\(≒0\)
- 負の相関:Sxy\(<0\)
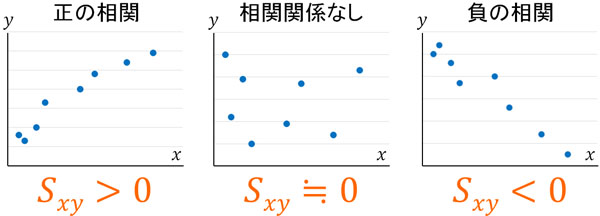
共分散がプラスなのかマイナスなのかによって、データの相関がどのようになっているのか把握できます。
・共分散を計算する
それでは、実際に共分散を計算してみましょう。例えば5人の体重と身長を測定して以下のデータが得られたとき、共分散の値はいくらでしょうか。
| 体重(kg) | 身長(cm) | |
| A | 64 | 170 |
| B | 70 | 178 |
| C | 66 | 162 |
| D | 58 | 166 |
| E | 82 | 184 |
統計データの処理はコンピューターが一瞬でしてくれます。一方で試験問題を解く場合、共分散を計算するために以下の表を作りましょう。
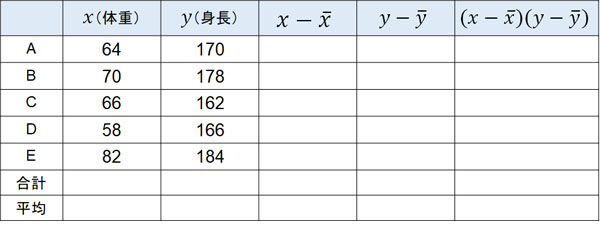
この表を完成させると、以下のようになります。
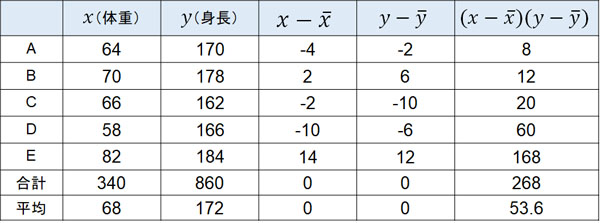
こうして、共分散は53.6と計算できます。
ピアソンの相関係数により、相関の強さを確認する
ただ共分散を利用しても、どれだけ強い相関があるのかわかりません。強い相関があるものの、平均値からの距離が小さいため、共分散の値が小さいことはよくあります。また弱い相関ではあるものの、平均値からの距離が遠いため、共分散の値が大きいこともあります。
つまり共分散を確認することによって正の相関なのか、負の相関なのか判断できるものの、相関の強さを判断することはできません。
例えば身長(cm)と体重(kg)のデータについて、身長の単位をcm(センチ)からm(メートル)にすると、共分散の値は1万分の1になります。そのため共分散の値がほぼ0であったとしても、強い相関をもつケースがあるのです。
そこで、相関の強さを示す指標があると便利です。そうした指標として、ピアソンの相関係数を利用します。「相関がある」というのは、一般的にピアソンの相関係数を指します。相関係数では、\(x\)の標準偏差(Sx)と\(y\)の標準偏差(Sy)を利用します。
\(x\)の偏差と\(y\)の偏差の積を考慮した値が共分散です。そこで相関係数(r)をだすとき、以下のように\(x\)の標準偏差と\(y\)の標準偏差をかけた後、割り算をしましょう。

共分散と「\(x\)の標準偏差と\(y\)の標準偏差のかけ算」を比べると、共分散のほうが値は小さくなります。共分散の場合、プラスやマイナスを含むデータをすべて足した後、平均値を出すことになります。
一方で分散をだすとき、全データを二乗することによってプラスに変えます。つまり分散を計算するとき、マイナスを含むデータを利用することはなく、プラスのデータをすべて足した後に平均値を出します。その後、分散の平方根を取ることによって標準偏差をだします。
プラスとマイナスを含む数の平均値(共分散)とプラスのみを含む数の平均値(標準偏差)では、標準偏差を利用するほうが値は大きくなるのです。
また前述の通り、正の相関ではSxy\(>0\)となります。一方で負の相関ではSxy\(<0\)となります。そのため、ピアソンの相関係数(r)は以下の範囲になります。
- \(-1≦r≦1\)
ピアソンの相関係数が1に近いと、強い正の相関があります。ただ相関係数が0に近づくと、相関が弱くなります。一方で相関係数が-1に近づくと、強い負の相関があるといえます。
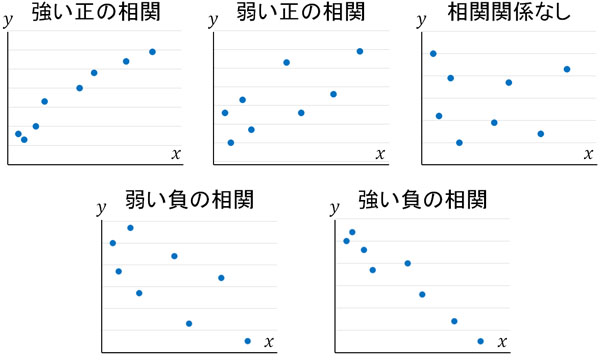
このように相関係数を利用することによって、正の相関や負の相関だけでなく、相関の強弱を知ることができます。
・ピアソンの相関係数を計算する
それでは、実際に相関係数を計算してみましょう。先ほど、体重と身長に関するデータの共分散を計算しました。このデータを利用して、次に相関係数を計算します。共分散の値はすでに出しているため、\(x\)と\(y\)の標準偏差(または分散)を出して、相関係数を計算しましょう。
そこで先ほどの表に対して、以下のように\(x\)と\(y\)の分散を加えます。
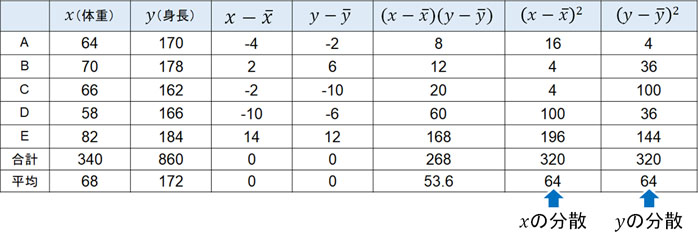
\(x\)の分散は64なので、\(x\)の標準偏差は8です。また\(y\)の分散は64なので、\(y\)の標準偏差は8です。\(x\)と\(y\)の共分散は53.6なので、以下のように相関係数を計算できます。
- \(r=\displaystyle\frac{53.6}{8×8}=0.8375\)
参考までに、ピアソンの相関係数を利用するとき以下のように考えます。
- 0.7~1.0:強い正の相関がある
- 0.4~0.7:正の相関がある
- 0.2~0.4:弱い正の相関がある
- -0.2~0.2:ほぼ相関関係なし
- -0.4~-0.2:弱い負の相関がある
- -0.7~-0.4:負の相関がある
- -1.0~-0.7:強い負の相関がある
先ほどのデータについて相関係数は0.8375であるため、強い正の相関があると判断できます。
相関係数は外れ値(異常値)の影響を受けやすい
それでは、相関係数の値が低い場合は必ず相関が弱いのでしょうか。統計データを処理するとき、相関係数のデメリットとして、外れ値(異常値)の影響を大きく受けることがあげられます。そのため非常に大きいデータ(または小さいデータ)が入ると、相関係数は大きく変動します。
これが相関係数のデメリットであり、データ数が少ないと異常値の影響をより受けやすくなります。例えば、先ほど計算したデータに「体重120kg、身長170cm」の人を加えてみましょう。肥満の人であれば、このようなケースは特に珍しくありません。その場合、以下のようなデータになります。
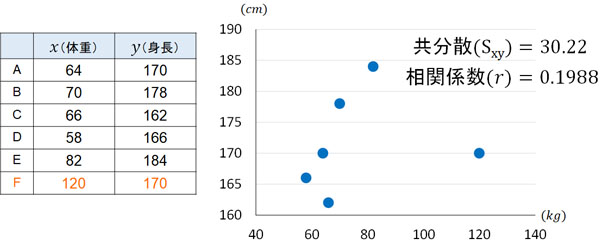
このように外れ値が一つ入ることによって、相関係数(r)は0.1988となり、相関関係はほぼないと判断されます。
どのようにデータを取り扱うのかによって、相関関係が出たり出なかったりします。統計データの処理方法によって結果が異なるのは、こうした理由があるのです。いずれにしても、「相関係数は外れ値の影響を受けやすい」というデメリットを理解しましょう。
相関があると、因果があるといえるのか?
また相関を理解するとき、ほかにも考慮しなければいけないポイントがあります。それは、「相関があると因果関係があるといえるのか?」という点です。
例えばデータを取ることによって、「月の平均気温が高いほど、アイスが多く売れる」というデータを得られたとします。このデータについては、月の平均気温と月のアイスの売上に相関関係があるように思えます。
それでは、「アイスが多く売れる月では、プールの来場者が多くなる」というデータはどうでしょうか。このデータについても、「気温が高いと多くの人がアイスを食べたり、プールに行ったりする」と推測できるため、因果関係があると予想できます。
一方、「交番が多い地域であるほど、治安が悪い」というデータについてはどうでしょうか。もしこのデータが本当なのであれば、交番がたくさんあるから治安が悪いのであり、交番の数を少なくしないといけません。
ただ実際には、人口が多い街であるため犯罪件数が多く、交番の数が多いのかもしれません。または、犯罪件数が多い地域のため、交番の数が多くなっているのかもしれません。つまり交番の数と犯罪件数に強い相関があっても、因果関係があるとはいえないのです。
疑似相関は頻繁に発生する
この事実を理解すると、統計データによって人をだませることに気づけます。統計では疑似相関が頻繁に発生します。つまり、実際にはまったく因果関係がないにも関わらず、相関関係が表れるのです。
例えばデータを取ると、「身長の高い人ほど、テストの点数が良い」という結果を得られたとします。この結果は直感的におかしいとわかります。つまり、データの集め方が間違っているために疑似相関を得られたというわけです。
例えば、先ほどのデータが「小学校1~4年生に受けさせた同じ内容のテスト」とわかればどうでしょうか。小学生なので、学年が高くなるほど身長は伸びます。また同じテストであれば、小学一年生に比べて、小学四年生はテストでよい点を取れます。
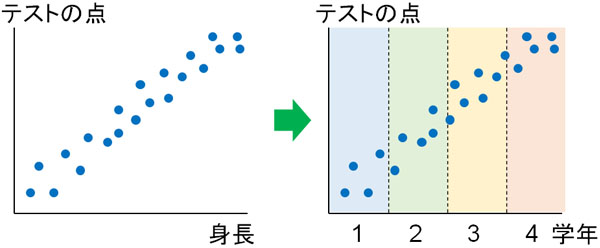
事実がわかると、明らかにサンプルの集め方を間違っていると判断できます。ただ統計データを処理すると、強い相関が表れます。
今回はわかりやすい疑似相関を例として解説しました。ただ疑似相関とすぐに判断できないデータを提示された場合、あなたはそれが本当かどうか判断できません。こうして、統計データというのは人をだますことにも利用されます。
この事実を知り、統計データに相関関係があるとしても、その中身が正しいのかどうか確認するようにしましょう。
散布図を確認し、共分散と相関係数を計算する
データに相関関係があるかどうかを調べるのは重要です。散布図を利用し、データに正の相関または負の相関がある場合、データに何かしらの関係性があると推測できます。
相関関係を調べるとき、利用される値に共分散と相関係数があります。共分散を利用すれば、正の相関なのか、それとも負の相関なのか判断できます。またピアソンの相関係数を利用すれば、相関の強さを判断できるようになります。
ただ統計データでは疑似相関が頻繁に表れます。つまり実際には因果関係がないにも関わらず、強い相関が表れるケースがあるのです。また外れ値があると、本当は強い相関があるにも関わらず、相関関係がないという結果になることもあります。
なお共分散や相関係数を計算するとき、これらの指標の意味を理解するだけでは不十分です。疑似相関を含め、統計データの欠点まで学びましょう。