統計学で学ぶ分布の一つに指数分布があります。ランダムに発生するイベントに対して利用されるのが指数分布です。
ランダムなイベント発生で利用されるため、多くの場面で指数分布は有用です。将来の発生確率を計算するとき、指数分布を利用するのです。
指数分布の累積確率分布を得ることができれば、時間経過と共に発生するイベントの確率がわかります。また公式を利用すれば、期待値(平均)や分散を得ることもできます。ほかには、指数分布には無記憶性という特徴もあります。
確率分布を学ぶとき、指数分布の特徴を理解しましょう。ここでは、指数分布の内容について解説していきます。
もくじ
ランダムなイベントの発生確率を表す連続確率分布
分布によって特徴が異なり、指数分布は連続型確率分布に分類されます。また、ランダムなイベントが発生するときに利用される確率分布です。
ランダムに発生するイベントとしては、例えば以下があります。
- 店舗へ客が来る
- 交通事故が発生する
- 機械が故障する
- 地震が発生する
- 街中で友人とすれ違う
このように、突発的に発生するイベントがどれくらいの確率で起こるのか推測できるのが指数分布です。
こうしたイベントは定期的に発生し、発生確率は常に一定と考えます。機械はいつか壊れますし、日本やインドネシアでは毎年地震が発生しています。そうした場合、指数分布に従うというわけです。
ポアソン分布と指数分布の違いは何か
なお指数分布の概要を学ぶと、多くの人は「ポアソン分布と何が違うのか」と疑問に思います。ポアソン分布についても、稀に発生するイベント(突発的なイベント)の確率を得ることができます。
指数分布では、次のイベント発生がいつ起こるのかについて確率を得ることができます。一方でポアソン分布では、特定の時間内に何回のイベントが発生するのかについて確率を得ることができます。つまり、次のような違いがあると考えましょう。
- 指数分布:次の発生間隔に着目する
- ポアソン分布:特定の時間内に発生するイベント回数に着目する
定期的に発生するイベントに対して、次回イベント発生の時間を調べたい場合は指数分布を利用します。
指数分布の確率密度関数の公式と意味
次に、指数分布の公式を確認しましょう。指数分布の確率密度関数は以下になります。
- \(f(x)=λe^{-λx}\)
恐らく意味を理解できないと思いますが、ひとまずこの公式を利用することによって確率密度を得ることができます。
\(λ\)というのは、特定の期間に発生するイベント回数を指します。そのため、イベントの種類によって\(λ\)は異なります。例えば1時間に平均5人が入店する場合、1時間を基準とするなら\(λ\)は5です。また1年に2回地震が発生する場合、1年を基準にするなら\(λ\)は2です。
特定の期間に平均して何度のイベントが発生するのか数えることによって\(λ\)が決まります。
また\(x\)は次のイベントが発生するまでの時間を指します。前述の通り、指数分布は次の発生間隔に着目します。そのため、次の発生時間として\(x\)を利用するのです。
・実際に指数分布の例題を解いてみる
そこで、実際に問題を解いてみましょう。そうすれば、指数分布が何を意味しているのか理解できるようになります。以下の問題の答えは何でしょうか。
- 1時間に平均5人が来店する店舗があります。10分後ピッタリに客が来店する確率密度はいくらでしょうか。
1時間に平均5人が来店するため、1時間を基準にすると\(λ=5\)です。また、10分後というのは\(\displaystyle\frac{10}{60}\)\(=\displaystyle\frac{1}{6}\)時間です。そこで、\(x=\displaystyle\frac{1}{6}\)を先ほどの公式に代入しましょう。
\(f(x)=5e^{-5×\displaystyle\frac{1}{6}}\)
\(≒2.17\)
こうして、確率密度は2.17になるとわかります。
指数分布のグラフはどのようになっているのか
それでは、指数分布のグラフはどのようになっているのでしょうか。先ほどと同じ条件について、\(x\)を変えてみましょう。つまり10分後だけでなく、ほかの部分の確率密度についても計算するのです。
この場合、以下のようになります。
| 経過時間 | 確率密度 |
| 5分後 | 3.30 |
| 10分後 | 2.17 |
| 20分後 | 0.944 |
| 30分後 | 0.410 |
| 40分後 | 0.178 |
| 50分後 | 0.0775 |
| 60分後 | 0.0337 |
このように、時間経過と共に確率密度は低くなっていきます。横軸を\(x\)、たて軸を確率密度とすると、以下のグラフを描くのが指数分布です。
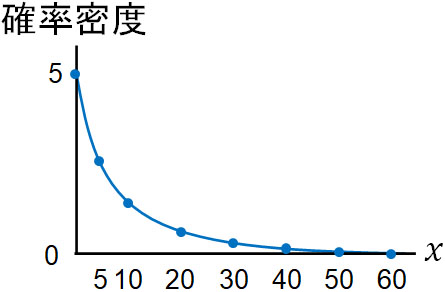
つまり指数分布では、次回のイベントが発生する確率密度は最初が高く、時間経過と共に確率密度が低くなると考えましょう。
なお\(λ\)によってグラフの形は変化します。具体的には、以下のようになると理解しましょう。
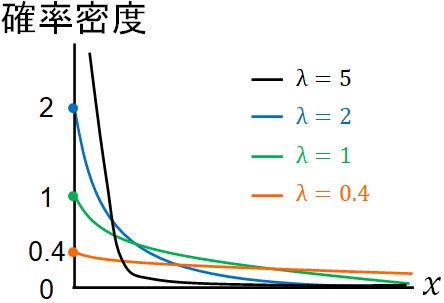
\(λ\)は時間ごとのイベントの平均発生回数であり、1時間を基準にするのか、それとも1年を基準にするのかによって\(λ\)の値は異なります。いずれにしても、このようなグラフの違いが表れます。
累積分布関数を利用し、確率を計算する
先ほど示した図は「特定の点での確率密度」です。ただ、特定の点での確率を知っても利用することはできません。指数分布では、それまでの確率分布をすべて足すことによって、確率がもつ意味をようやく理解できるようになります。
当然ながら、時間経過と共にイベントの発生確率は高くなります。例えば一定間隔で交通事故が起きるにも関わらず、長く交通事故が起きていない場合、交通事故が発生する確率は高くなります。
そこで特定のポイントの確率密度ではなく、「特定のポイントについて、それまでの確率密度をすべて累積した値」を計算してみましょう。特定のポイントについて、すべての発生確率を足すことによって得られる関数を累積分布関数\(F(x)\)といいます。
ランダムで発生するイベントについて、時間経過が長くなると再び発生する確率が高くなるのは、私たちの感覚にも合致します。これは、すべての確率を足すことで可能になるのです。
連続型確率分布は曲線のグラフです。この場合、積分を用いて面積を計算しましょう。面積を得ることによって、すべての確率密度を足すことになります。つまり、面積が累積分布関数になります。そこで、以下のように計算しましょう。
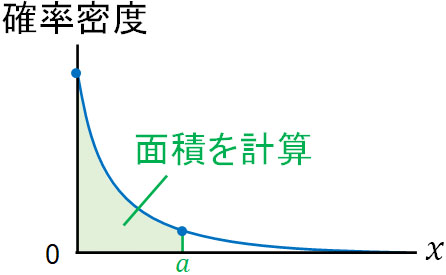
\(F(a)=\displaystyle \int_{0}^{a} λe^{-λx} dx\)
\(=1-e^{-λa}\)
こうして、累積分布関数は\(F(x)=1-e^{-λx}\)とわかりました。これをグラフにすると以下のようになります。
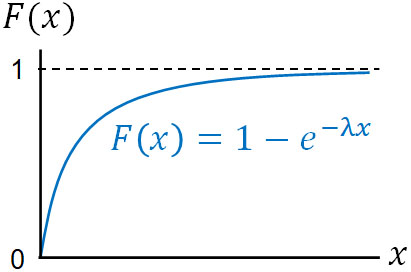
指数分布を利用して次のイベントが発生する確率を知りたい場合、特定のポイントでの発生確率よりも、累積分布関数を利用するほうが私たちにとって理解しやすいです。
それでは、先ほどの例題について累積分布関数を利用して問題を解いてみましょう。
- 1時間に平均5人が来店する店舗があります。10分後までに客が来店する確率はいくらでしょうか。
10分後ピッタリに客が来店する確率密度ではなく、10分が経過するまでに客が来店する確率を計算します。この場合、累積分布関数を利用しましょう。\(λ=5\)であり、\(x=\displaystyle\frac{1}{6}\)なので以下のようになります。
\(1-e^{-\frac{5}{6}}≒0.565\)
こうして、確率密度の合計(面積)は0.565(56.5%)とわかります。こうして、客が来店する確率を計算できます。
期待値(平均)の計算と公式
それでは、指数分布の期待値(平均)はどのように計算すればいいのでしょうか。指数分布を利用するとき、以下の公式によって期待値\(E(X)\)を計算できます。
- \(E(X)=\displaystyle\frac{1}{λ}\)
ただ、この公式は感覚的に理解できます。例えば1時間に平均5人が来店する場合、平均して\(\displaystyle\frac{1}{5}\)時間ごとに客が来ると推測できます。単位時間あたりに\(λ\)回のイベントが発生する場合、期待値が\(\displaystyle\frac{1}{λ}\)になるのは当然です。
なお期待値の定義を利用すると、以下のように証明できます。
\(E(X)=\displaystyle \int_{0}^{\infty} xf(x) dx\)
\(=λ\displaystyle \int_{0}^{\infty} xe^{-λx} dx\)
\(=\left[-xe^{-λx}\right]_0^{\infty}+\displaystyle \int_{0}^{\infty} e^{-λx} dx\)
\(=0+\left[-\displaystyle\frac{1}{λ}e^{-λx}\right]_0^{\infty}\)
\(=\displaystyle\frac{1}{λ}\)
高校数学の知識を利用することにより、期待値\(E(X)\)が\(\displaystyle\frac{1}{λ}\)と証明できました。ただこうした証明をしなくても、感覚的に指数分布の期待値(平均)は\(\displaystyle\frac{1}{λ}\)とわかります。
指数分布で分散の計算を行う
なお期待値の計算をした後、次に分散の計算を行えるようにしましょう。指数分布の場合、期待値と同じように分散の公式も単純です。以下が指数分布で分散\(V(X)\)を得る公式です。
- \(V(X)=\displaystyle\frac{1}{λ^2}\)
分散の証明については、分散の定義を利用しましょう。つまり、以下の公式を利用します。
- \(V(X)=E(X^2)-E(X)^2\)
\(E(X)=\displaystyle\frac{1}{λ}\)であるため、\(E(X)^2=\displaystyle\frac{1}{λ^2}\)です。そこで、\(E(X^2)\)を求めましょう。
\(E(X^2)=λ\displaystyle \int_{0}^{\infty} x^2e^{-λx} dx\)
\(=\left[-x^2e^{-λx}\right]_0^∞+\displaystyle \int_{0}^{\infty} 2xe^{-λx} dx\)
※\(λ\displaystyle \int_{0}^{\infty} xe^{-λx} dx=\displaystyle\frac{1}{λ}\)より
\(=0+\displaystyle\frac{2}{λ^2}\)
\(=\displaystyle\frac{2}{λ^2}\)
こうして、以下のように分散\(V(X)\)を計算できます。
\(V(X)=E(X^2)-E(X)^2\)
\(=\displaystyle\frac{2}{λ^2}-\displaystyle\frac{1}{λ^2}\)
\(=\displaystyle\frac{1}{λ^2}\)
指数分布には無記憶性がある
なお指数分布には無記憶性があります。離散型確率分布の場合、幾何分布のみ無記憶性があります。一方で連続型確率分布の場合、無記憶性を有するのは指数分布だけになります。
無記憶性とは、過去に起こった出来事が将来の確率に影響しないことを指します。
例えば1時間で平均5人が来店する店について、1時間で20人の来店があったとします。このとき、「今日は既に多くのお客さんが来店しているため、この後は客数が少なくなる」とはなりません。たまたま団体客が入店したために客数が多くなっている場合、その後の来店客数はいつもと同じです。
また電化製品を修理した後、すぐに壊れないとは限りません。不具合があれば、修理した次の日に再び故障することもあります。
定期的に発生する稀なイベントについて、過去の出来事が反映されない事実は私たちが日常的に感じています。これが無記憶性であり、連続型確率分布では指数分布に特有の性質です。なお、指数分布での無記憶性は以下の数式によって表されます。
- \(P(X>s+t|X>s)\)\(=P(X>t)\)
恐らく、まったく意味を理解できないと思います。ただ数式を理解する必要はなく、「指数分布には無記憶性がある」と理解すれば問題ありません。なお無記憶性の証明をしたい場合、条件付き確率を利用して証明してみましょう。
指数分布を利用し、発生頻度を計算する
定期的に発生するイベントに対して、指数分布を利用すれば発生頻度を計算できるようになります。単位時間ごとの平均発生回数\(λ\)と経過時間\(x\)を利用することによって確率密度を出せます。
また累積分布関数を利用すれば、特定の時間までに発生する確率を得ることができます。特定期間内のイベント回数に着目するポアソン分布とは異なり、指数分布では次回の発生間隔に着目します。
なお、指数分布の期待値(平均)を得る公式はシンプルです。分散についても単純な公式を利用して計算できます。それに加えて、指数分布には無記憶性があることを理解しましょう。連続型確率分布の中でも、無記憶性をもつのは指数分布だけです。
ランダムでイベントが発生するケースは多いです。そうした場合、指数分布を利用することによって発生確率を計算できるようになります。