一つの操作をするとき、どのような結果を得られるのか予測するための指標として期待値があります。期待値を確認することによって、将来の結果を予測できるのです。
期待値を計算するために理解しなければいけないのが確率変数と確率分布です。確率変数と確率分布を利用することによって期待値の計算ができます。また期待値を利用すれば、あるゲームに参加するのが有利なのか、それとも不利なのか判断できるようになります。
また確率変数の期待値について、分散と標準偏差を計算できるようになりましょう。どれだけのばらつきがあるのか表すのが分散と標準偏差です。
統計学を専攻している人に限らず、多くの人にとって期待値の概念は重要です。そこで期待値をどのように計算し、分散と標準偏差を求めればいいのか解説していきます。
もくじ
確率変数・確率分布とは何か
まず、確率変数や確率分布とは何なのでしょうか。一つの操作をするとき、取り得る値を確率変数といいます。
例えばサイコロを投げるとき、取り得る値は1~6です。そのため一つのサイコロについて、確率変数は1~6までの数です。

それでは、特定の確率変数になる確率はいくらでしょうか。サイコロの場合、すべての数字について\(\displaystyle\frac{1}{6}\)の確率で表れます。そのため以下の表を作ることができます。
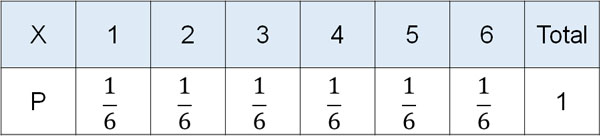
この表について、Xを確率変数といいます。またXに対応する確率を確率分布といいます。そのため確率分布を求めるためには、上の表を作成すればいいと理解しましょう。
確率分布の表を作る:確率の総和は必ず1になる
先ほどはサイコロを利用し、簡単な確率分布の表を作成しました。それでは、少し複雑な場合の確率分布の表はどのようになるのでしょうか。以下の問題を解いてみましょう。
- 目の数が「2,2,4,4,5,6」の特製サイコロがあります。このサイコロを投げるとき、確率分布はどのようになるでしょうか。
一般的なサイコロとは異なり、1と3の目がありません。そのため、確率変数は2,4,5,6の4つになります。またそれぞれの確率変数に対する確率を計算すると、確率分布を得ることができます。以下のようになります。
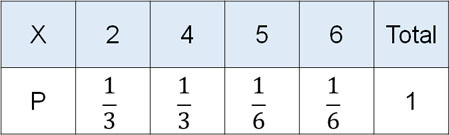
特殊なサイコロを利用することになるため、2の目が出る確率は\(\displaystyle\frac{1}{3}\)です。また4の目が出る確率は\(\displaystyle\frac{1}{3}\)です。そのため、このような確率分布になります。
重要なのは、確率の総和は必ず1(100%)になることです。起こるすべての事象を足すと、当然ながら1にならなければいけません。確率分布の表を作るとき、確率P(Probability)の合計が1でない場合、必ず間違っていることを理解しましょう。
確率変数の期待値の計算方法
確率変数や確率分布を理解したら、次に期待値を計算できるようになりましょう。期待値というのは、一つの操作をするとき、得られるであろう予想値です。
例えば普通のサイコロを投げるとき、出る目の期待値はいくらでしょうか。サイコロを投げると、1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。また2の目が出る確率は\(\displaystyle\frac{1}{6}\)です。同じように、1~6まですべての値について\(\displaystyle\frac{1}{6}\)の確率で出ます。
そこで確率変数と確率を掛け合わせた後に足しましょう。以下のようになります。
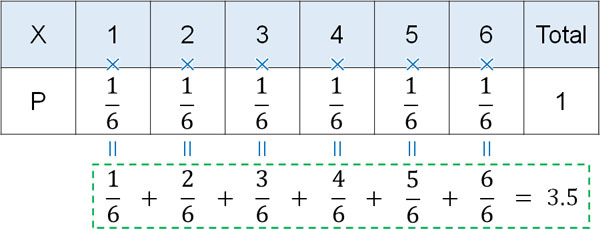
この計算によって得られる値(3.5)が期待値です。確率変数と確率をかけ算し、足すことによって期待値を得られます。期待値が3.5であるため、「サイコロを振るとき、出る目は3.5になると期待できる」というわけです。
サイコロの目に3.5はないため、当然ながら一回サイコロを投げて3.5になることはありません。また、サイコロの目が2になることがあれば、6になることもあります。
ただ何度もサイコロを投げ、出る目の平均値を計算すると、必ず3.5に収束するようになります。期待値というのは、「一つの操作をすることによって、どのような結果を得られるのか」についての平均値を指します。
もしサイコロを投げて3となる場合、期待できる値よりも低い結果になったといえます。またサイコロを投げて4となる場合、平均よりも高い値を得たとわかります。このように期待値というのは、「確率を利用するときの結果の平均値」と理解しましょう。
そのため確率分布が異なると期待値も変化します。例えば先ほどの「2,2,4,4,5,6」の特製サイコロの場合、期待値はどのようになるでしょうか。確率分布を利用して期待値を計算すると以下のようになります。
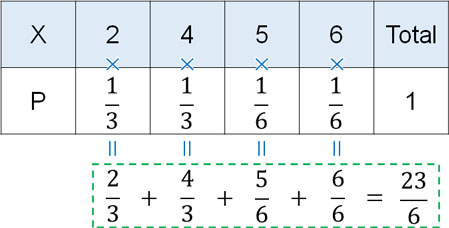
つまり一回サイコロを投げ、出てくる値は\(\displaystyle\frac{23}{6}\)になると期待できます。確率変数の期待値を計算するとき、このように計算しましょう。
期待値の公式の意味を理解する
ここまでの内容を理解すると、期待値の公式の意味を理解できるようになります。例えば以下のような確率分布があるとします。

先ほどと同じように期待値を計算する場合、確率変数と確率をかけ算して足せばいいため、以下のように表すことができます。
- 期待値\(=X_1P_1+X_2P_2+…+X_nP_n\)
またすべてを合計するとき、数学では\(σ\)を利用して表します。そのため、先ほどの公式を以下のように記すこともできます。
- 期待値\(=\displaystyle \sum_{k=1}^n X_kP_k\)
ただ、この公式を覚える必要はありません。そうではなく、「期待値が何を意味しているのか」「どのように計算するのか」を理解しましょう。そうすれば、公式なしに期待値を計算できます。
統計学というのは、公式を見ても理解できないケースがほとんどです。また実際のところ、どのように計算すればいいのか理解し、公式なしに問題を解けるようにするべきです。そのため期待値の計算をするとき、公式なしに答えを出せるようにしましょう。
期待値を利用し、有利・不利を確認する
なお期待値を理解すれば、特定のゲームについて参加するときに有利なのか、それとも不利なのか判断できるようになります。
例えば、以下の問題の答えは何でしょうか。
- お小遣いをもらうとき、毎日100円をもらうことができます。または「サイコロを毎日投げ、1の目がでると500円、その他の目の場合は60円をもらう」という方法を選択することもできます。どちらが有利でしょうか。
この問題を解くため、期待値を計算しましょう。サイコロを利用するため、以下のように期待値を計算できます。
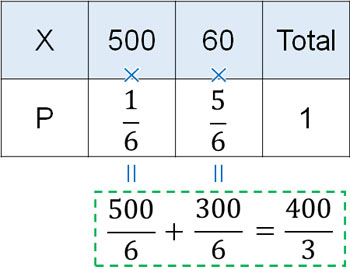
このように、期待値は\(\displaystyle\frac{400}{3}\)になります。また\(\displaystyle\frac{400}{3}\)は100よりも数字が大きいです。また毎日サイコロを振ることになるため、得られるお小遣いは一日あたり\(\displaystyle\frac{400}{3}\)円に収束します。
つまり、毎日100円をお小遣いとしてもらうのではなく、サイコロを振るほうが有利です。このように期待値を利用することによって、有利・不利を判断できます。
期待値というのは日常生活のあらゆる場面で利用されています。例えば株式投資をするとき、米国株と中国株について、どちらに投資をするほうがお金を増やすことができるのでしょうか。米国株と中国株について、過去の株価推移を比較すると以下のようになります。
・米国株(S&P500)
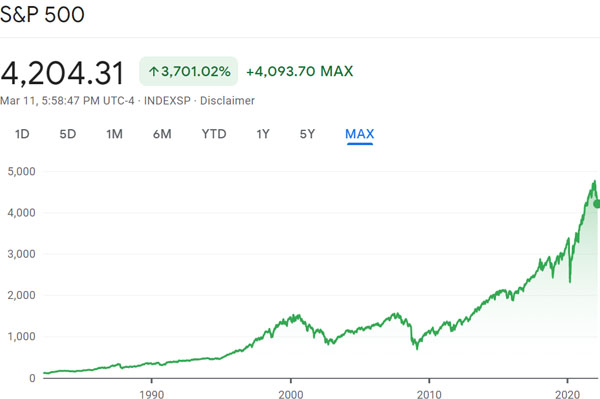
・中国株(上海総合指数)
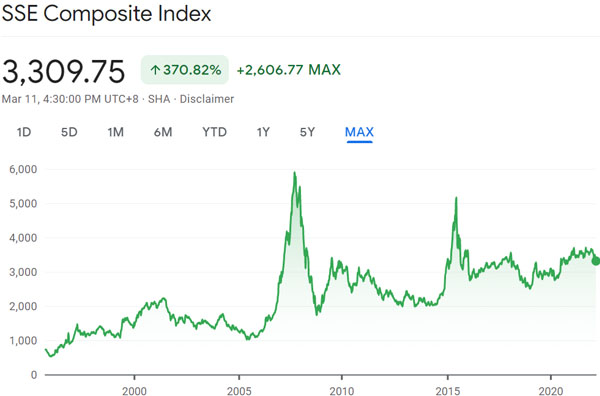
このように米国株(S&P500)は長期的にずっと上昇しており、投資によってほぼ確実に資産を増やせるとわかります。一方で中国株(上海総合指数)は株価がほぼ上昇しておらず、期待値が非常に低いです。計算方法によっては、中国株では期待値がマイナスとなります。
ゲームに一回参加するだけの場合、得をするのか損をするのかは運です。ただ何度もゲームに参加する場合、高い期待値を得られるゲームに参加すれば、当然ながら資産を増やせるというわけです。
確率変数の期待値での分散と標準偏差
ここまでの内容を理解したら、次に期待値を利用して分散と標準偏差を計算できるようになりましょう。統計データについて、ばらつきを表すのが分散と標準偏差です。
一般的な分散の計算では、平均値を利用して計算します。例えば、以下のデータがあるとします。
- 0, 6, -1, 3, 8, 2
このデータについて、平均値は3です。そこで平均値(3)からの距離をそれぞれ計算します。ただ平均値からの距離を測定すると、正の値と負の値が出てしまいます。そこで平均値からの距離について二乗し、正の値を得るようにします。
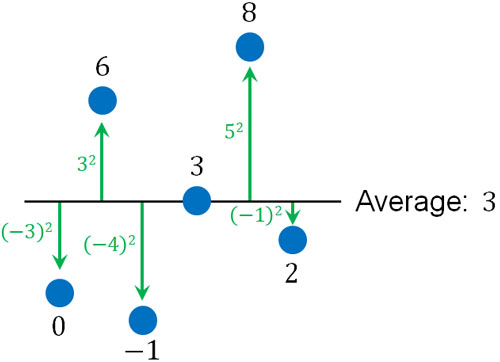
「平均からの距離を二乗した値」の平均値が分散です。平均値を出すため、二乗した値をすべて合計し、個数で割ることで分散を得ることができます。
\(\displaystyle\frac{(-3)^2+3^2+(-4)^2+5^2+(-1)^2}{6}=10\)
また二乗した値が分散であるため、平方根を利用することによって二乗を取り去ることができます。分散に対して平方根を加えたものが標準偏差です。

これらの基本的な知識を利用して期待値の分散と標準偏差を計算しましょう。
期待値に対する分散と標準偏差を計算する
期待値というのは、前述の通り「確率での平均値」です。つまり平均値として期待値を利用すれば、分散を計算できます。なお期待値を\(E(X)\)とするとき、分散を\(V(X)\)、標準偏差を\(σ(X)\)と表します。
それでは、目の数が「2,2,4,4,5,6」の特製サイコロについて、分散\(V(X)\)と標準偏差\(σ(X)\)は何でしょうか。先ほど、このサイコロの期待値は\(\displaystyle\frac{23}{6}\)と計算しました。そこで期待値\(E(X)\)を利用し、分散\(V(X)\)と標準偏差\(σ(X)\)を計算してみましょう。
期待値を利用して分散を計算する場合、以下のようになります(詳細な分散の計算方法は説明を省きます)。

なお標準偏差は平方根を利用すればいいため、以下のようになります。
\(\sqrt{\displaystyle\frac{77}{36}}=\displaystyle\frac{\sqrt{77}}{6}\)
期待値を利用してこのように計算するため、期待値を\(m\)とすると、以下の公式を作ることができます。

この公式についても覚える必要はなく、ここまで解説した「期待値の分散を計算する方法」を理解するようにしましょう。
公式を変形し、分散を出すための新たな公式を得る
ちなみに、先ほどの公式を変形することによって以下の公式を導くことができます。
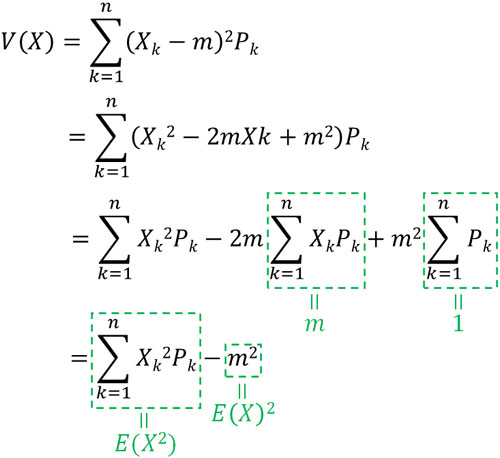
こうして、分散を得る以下の公式を出すことができました。
- \(V(X)=E(X^2)-E(X)^2\)
この公式を利用して分散の計算をしたい場合、公式を覚えなければいけません。公式を利用しなくても先ほどの計算方法によって分散を出すことはできるものの、コンピューターではなくあなたが計算する場合、この公式を利用すると計算は楽になります。
この公式は何を意味しているのでしょうか。\(E(X^2)\)というのは、「\(X^2\)の期待値」を表します。つまり、\(X^2\)を利用して「\(X^2\)の期待値」を出しましょう。
また\({E(X)}^2=m^2\)であり、要は期待値を二乗した値を指します。そのため目の数が「2,2,4,4,5,6」の特製サイコロについて、期待値\(\displaystyle\frac{23}{6}\)を利用して以下のように分散を計算できます。

こうして、先ほど計算した分散\(V(X)\)と同じ値を得ることができます。また分散が同じであるため、標準偏差\(σ(X)\)も同じです。
分散の計算では方法(公式)が2つあり、どちらの公式を利用しても問題ありません。いずれにしても期待値の分散と標準偏差について、意味や計算方法を理解しましょう。
確率分布を利用し、確率変数の期待値を得る
統計学を学んでいない場合、確率変数や確率分布という言葉を新たに学ばなければいけません。ただ概念は簡単であり、確率変数に対応する確率を表すのが確率分布です。また確率分布を利用することによって、確率変数の期待値を得ることができます。
期待値というのは、要は平均値です。一つの操作をするとき、どのような結果を得られるのか平均値を計算すれば、それが期待値になります。
期待値は確率を用いる平均値でもあるため、期待値を利用することによって分散と標準偏差を出すことができます。計算方法(公式)は2つあるため、分散を求めるときにはどちらの方法を利用しても問題ありません。
なお公式を覚えても計算できるようになることはないため、確率変数や確率分布、期待値、分散、標準偏差の意味や計算方法を理解しましょう。これにより、統計での計算ができるようになります。