有意水準とp値：帰無仮説・対立仮説での有意差と両側検定・片側検定

なぜ多くの人が統計学を学ぶかというと、得られたデータに差があるかどうかを確認したいからです。データを集めたとき、データに差がある（または差がない）ことを客観的に証明するためには統計処理が必要です。

差があることを有意差といいます。5%や1%などを利用することによって、どれだけ差があるのかを示すのです。このとき使われる言葉が有意水準やp値、有意差です。

また差があることを述べるためには、帰無仮説と対立仮説を利用しなければいけません。また両側検定をしたいのか、それとも片側検定をしたいのかによって統計処理の方法も異なります。

統計処理が可能になれば、データが意味あるのかどうかを判断できるようになります。そこでデータを集めた後、差があることを述べるためにどう考えればいいのか解説していきます。

1 有意水準、p値、有意差の違い
- 1.1 95%信頼区間（99%信頼区間）を利用し、有意差を確認する
- 1.2 両側検定または片側検定で判断する
2 検定での帰無仮説・対立仮説とは何か
- 2.1 p値（確率）を計算し、有意差があるかどうかを判断する
- 2.2 コインを10回投げ、表が1回出るときのp値
3 帰無仮説・対立仮説を利用し、有意差を結論付ける

有意水準、p値、有意差の違い

まず有意水準やp値、有意差の違いを理解しましょう。これらの言葉について、以下の順番でデータ処理することになります。

有意水準
p値
有意差

最初に決めなければいけないのは有意水準です。有意水準とは、基準と考えましょう。例えばBMI（Body Mass Index）を利用する場合、値が30以上の場合は肥満と判断されます。

差があるかどうかを判断するためには、最初に基準を設定しなければいけません。そこで有意水準を設けるのです。

次に計算するのがp値です。pはProbability（確率）のことであり、観測された事象が起こる確率を表します。起こる確率がp値であることを理解すると、特に難しい単語ではありません。

有意水準を決め、p値を求めたら、次に有意差を確認します。有意水準というのは、有意差を判断するための基準です。そこで有意水準とp値を比較し、p値が有意水準のよりも大きい値なのか、それとも小さい値なのかを確認することで有意差の有無を判断します。

95%信頼区間（99%信頼区間）を利用し、有意差を確認する

それでは有意水準はどのように決めるのでしょうか。有意水準は事前に決めなければいけません。そうでないと、データを自由に操作できてしまうからです。

例えば製品のテストをするとき、性能が80点であれば合格であるとします。ただ実際に性能をチェックした後、性能が75点であればどうでしょうか。この場合、合格基準を70点に落とせば合格してしまいます。こうして、結果を自由に操作できてしまいます。基準を最初に決めないといけないのは、このような意図的な操作を防ぐためです。

なお統計処理については、有意水準は決まっています。具体的には0.05（5%：95%信頼区間）または0.01（1%：99%信頼区間）を利用します。

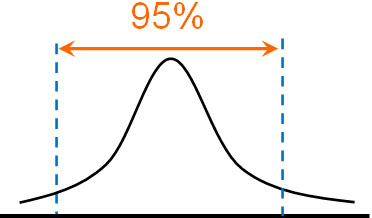
データを集めて統計処理するとき、データ全体の95%（または99%）から逸脱している場合、「何かしら差がある」と判断できます。

差があることを述べるとき、何を測定するのかによって意味が異なります。例えば、「異常がある」「薬に効果がある」「イカサマをしている」「性能が優れている」など利用するデータによって意味が変わります。

両側検定または片側検定で判断する

このとき、有意差の判定で0.05（5%：95%信頼区間）または0.01（1%：99%信頼区間）を利用するにしても、両側検定をするのか、それとも片側検定をするのかを決めましょう。

両側検定とは、グラフの両側を利用することで検定を行うことを指します。例えば0.05を有意水準にする場合、グラフの左側0.025（2.5%）と右側0.025（2.5%）を合わせて0.05（5%）に設定する必要があります。

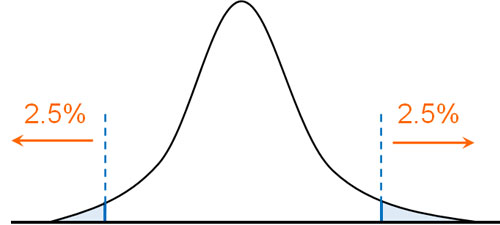
例えば「1歳の子供について、体重が異常な子供に対して通知したい」という場合、どのように判断すればいいでしょうか。異常な体重というのは、「体重が軽い」「体重が重い」の2種類があります。この場合、両側検定によって判定します。

一方、片側のみを判断するケースも頻繁にあります。この場合はグラフの片側のみを判断するため、グラフの左側0.05（5%）またはグラフの右側0.05（5%）を利用して判断します。

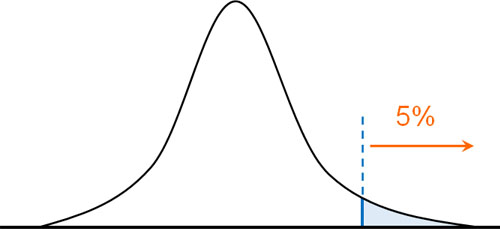
例えばテストの成績が優れているかどうか判断するとき、片側検定をします。テストの点数では、点数の良い人がいれば、点数の悪い人もいます。

成績が優れているかどうかを判定するとき、点数の悪い人を無視して、点数の良い人を基準にしなければいけません。そのため、片側検定によってグラフの片側の5%に含まれるかどうかを確認するのです。

参考までに、両側検定と片側検定では、両側検定のほうが厳しい条件での検定になります。片側検定に比べて、右側（または左側）の面積が狭く、棄却域が狭いからです。ただ両側検定で有意差を得られなかったとしても、片側検定でやり直してはいけません。その場合、人間による意図的な操作が入ることになるからです。

検定での帰無仮説・対立仮説とは何か

なお実際にデータの検定をするとき、必ず出てくる言葉に帰無仮説と対立仮説があります。帰無仮説と対立仮説とは何なのでしょうか。

統計的検定をするとき、差があることを証明するためには、以下を説明する必要があります。

差がないことを否定することによって、差があることを証明する

実際のところ、差があることを直接証明するのは難しいです。あなたは差があると思っても、ほかの人は差がないと思うかもしれません。そこで、最初に「データには差がない」という仮説を立てます。その後、この仮説を否定することができれば、結果的に「データには差がある」と証明できます。

数学でいう背理法に似ている考え方をすることによって、データに差があることを述べるのが統計学での検定です。このとき、以下のような仮説を利用します。

差がない仮説：帰無仮説
差がある仮説：対立仮説

示したい仮説が対立仮説です。「製品は優れている」「薬に効果がある」「業務効率が向上する」など、何かしかの効果を示すために私たちは統計処理をします。

それに対して、帰無仮説では対立仮説の逆を述べます。例えば「製品に差はない」「薬に効果はない」「業務効率は改善しない」などです。そこで帰無仮説を否定できれば、結果として対立仮説を採用できるというわけです。

一方で「帰無仮説を棄却する」という証明方法ではなく、「対立仮説を棄却できない」という方法での証明ではどうでしょうか。この場合、例えば「製品が優れていることを棄却できない」となります。

この場合、製品は優れているかもしれないし、優れていないケースもあります。要は、何の結果も得られていないことを意味します。そのため差があることを証明するためには、「差がないことを否定する」ことでのみ可能なのです。

統計処理で必ず帰無仮説と対立仮説を利用するのは、こうした理由があります。差がないことを否定することによって、結果として差があることを証明できるのです。

p値（確率）を計算し、有意差があるかどうかを判断する

検定をするとき、いくつもの方法があります。t分布を利用する場合、t検定と呼ばれます。カイ二乗分布を利用する場合、カイ二乗検定と呼ばれます。二項分布を利用する場合、二項検定と呼ばれます。確率計算をするとき、どの方法を採用するのかによって検定の名前が変わります。

ただ基本的な考え方は同じであり、以下の順番によって検定をします。

帰無仮説を設定する
確率を計算する
帰無仮説を棄却できるかどうか判断する

それでは実際にp値を計算し、差があるかどうかを確認しましょう。以下のケースについて、差はあるでしょうか。

コインを10回投げ、表が2回出ました。これは偶然でしょうか。

通常、コインを投げて表と裏が出る確率はそれぞれ\(\displaystyle\frac{1}{2}\)です。ただイカサマがある場合、コインが表になる確率は高いです。

そこで、まずは以下のように帰無仮説と対立仮説を立てましょう。

帰無仮説：コインを投げるとき、イカサマはない
対立仮説：コインを投げるとき、イカサマがある

イカサマがない場合、前述の通り表が出る確率は\(\displaystyle\frac{1}{2}\)です。そこでp値を計算しましょう。

p値というのは、観測されたデータに加え、それよりも極端な値が観測される確率を指します。今回、イカサマがない場合、コインを10回投げて表が2回出る確率は以下になります。

\(_{10}C_2\left(\displaystyle\frac{1}{2}\right)^2\left(\displaystyle\frac{1}{2}\right)^8≒0.0439\)

ただ、この値がp値ではありません。極端なケースも考慮する必要があるため、「10回コインを投げ、表が1回または0回のケース」も考慮しなければいけません。つまりp値というのは、結果よりも極端なケースをすべて含む確率の合計を指します。それ以上（またはそれ以下）の結果を得られる確率も足さなければいけません。

そこで表が出る場面ではなく、裏が2回（または1回、0回）のケースも考慮しましょう。10回のコインを投げ、裏が出る回数が多い場合についてもイカサマを疑う必要があります。そのため片側検定ではなく、両側検定によって判断しましょう。

つまり、以下の確率をそれぞれ計算してすべて足します。

コインを10回投げ、表が0回出る確率
コインを10回投げ、表が1回出る確率
コインを10回投げ、表が2回出る確率
コインを10回投げ、裏が0回出る確率
コインを10回投げ、裏が1回出る確率
コインを10回投げ、裏が2回出る確率

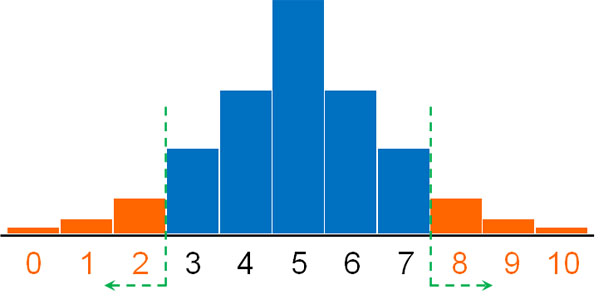
今回は二項分布を利用して確率を計算します。実際の計算は省きますが、「コインを10回投げて表が2回出るケースに加え、より極端なケースが出るケースも含めた確率」は約0.109です。つまり10.9%の確率でこのような結果を得られます。

有意水準を0.05（5%）とすると、p値は0.109（10.9%）であるため、帰無仮説を棄却できません。つまり、偶然起こった現象であると判断できます。帰無仮説を棄却できないため、必ずしもイカサマがあるとはいえないのです。

コインを10回投げ、表が1回出るときのp値

一方でコインを10回投げるとき、表が2回ではなく、1回出る場合はどうでしょうか。この場合、二項分布を利用して、以下の確率をすべて足しましょう。

コインを10回投げ、表が0回出る確率
コインを10回投げ、表が1回出る確率
コインを10回投げ、裏が0回出る確率
コインを10回投げ、裏が1回出る確率

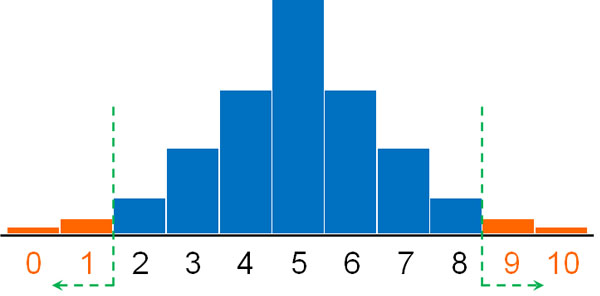
細かい計算は省きますが、すべての確率を足すとp値は約0.021（2.1%）となります。

有意水準が0.05（5%）であれば、p値が0.05以下となるため、帰無仮説を棄却できます。つまり、偶然に起こる現象と考えることはできず、コインにイカサマがあると統計学的に主張できるのです。

今回の結果が得られる確率は5%未満です。このような起こる確率の低い事象が偶然に起こるとは考えにくいため、帰無仮説が間違っていると考え、対立仮説を採用するというわけです。また帰無仮説を棄却できる場合、有意差があると判断できます。

有意水準（5%または1%）よりもp値が小さい場合、帰無仮説を棄却し、有意差ありと判断します（今回のケースでは、コインにイカサマがあると判断する）。一方で有意水準よりもp値が大きい場合、有意差はなく、偶然に起こった事象と考えます。有意差というのは、有意水準とp値を比較することによって決定されるのです。