私たちは毎日、波を感じています。音は波によって伝わりますし、海に行けば波が海岸へ打ち寄せています。また、機器類は電波を受信します。物理で波動を学ぶのは、波があらゆる場面で関わっているからなのです。
波動を学ぶためには、波の性質だけでなく、振動数や周期、波長の概念を理解しなければいけません。これらを得るための公式を学ぶのです。
また振動数や周期、波長の概念がわかれば、波の式を作ることができます。公式を覚えても波の式を作ることはできないため、公式の導き出し方を理解しましょう。また波には横波と縦波があるため、それぞれの性質を把握しなければいけません。
それでは、波の性質には何があるのでしょうか。また、どのように公式を利用すればいいのでしょうか。波動の性質や波の式について解説していきます。
もくじ
波の性質:振動が周囲に伝わる
海で波が海岸へ打ち寄せている様子をみると、波は横へ動いているように思ってしまいます。ただ実際には、波は横へ動いていません。より正確にいうと、波は上下に振動するものの、横には動きません。
先ほど、音は波であると解説しました。波には、振動や変化を周囲に伝える性質があります。音波として空気中を伝わることにより、音が私たちの耳で聞こえるのです。
ただ音波が伝わるとき、波は振動を伝えるだけであり、横には動きません。音は秒速340mであるものの、音が伝わるときに秒速340mの風を生じることはありません。これは、音は振動として周囲に性質を伝えるものの、横には移動しないからです。
例えば、ロープを固定して揺らすと、下図のように波が生まれます。
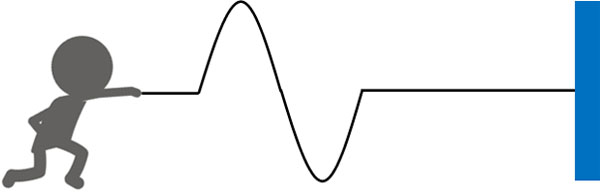
このときロープの一点だけに着目すると、その点は上下に振動しているものの、横には動いていません。
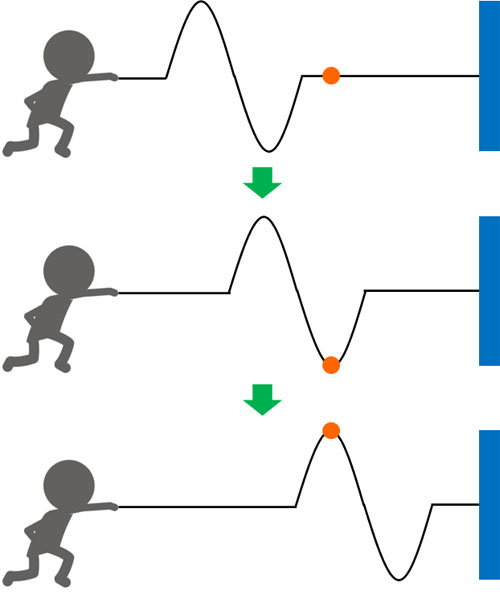
例えば「下に移動する」という性質が来たら、点は下に移動します。その後、「上に移動する」という性質が伝われば、点は上に移動します。こうして、性質が伝わっていくのが波なのです。
時間ごとの波の様子を表す\(y-x\)グラフと\(y-t\)グラフ
波の動きを確認するとき、波動では2つのグラフを使い分けましょう。波では\(y-x\)グラフと\(y-t\)グラフの2つを利用します。
特定の時間での波の形を表すのが\(y-x\)グラフです。\(x\)軸は距離を表し、\(y\)軸は上下の幅を表します。
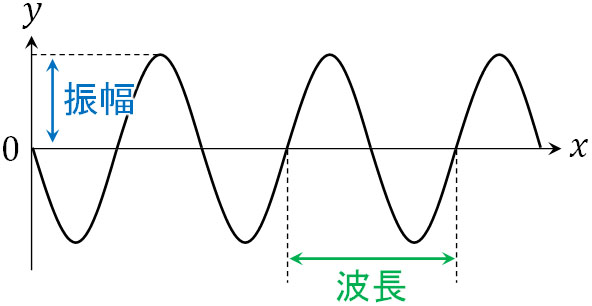
このとき、\(y\)軸での0から最大値(または最小値)までの距離が振幅(しんぷく)です。また、波は上下を繰り返します。そこで、上下の振動1セットを1つの波と考えるとき、この長さを波長といいます。\(y-x\)グラフでは横軸が長さであるため、上下の振動1セットが波長になるのです。なお波長はλ(ラムダ)で表し、単位はメートルです。
・\(y-t\)グラフから振幅と周期を読み取る
\(y-x\)グラフに対して、横軸を距離ではなく時間\(t\)に設定したグラフが\(y-t\)グラフです。つまり\(y-t\)グラフでは、特定の点について、経過時間\(t\)による波の変化を表します。以下が\(y-t\)グラフです。
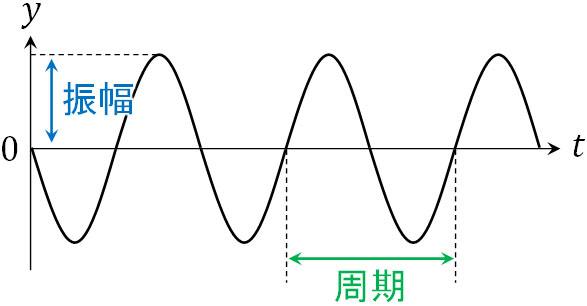
\(y-x\)グラフと\(y-t\)グラフを比べると、見た目は同じです。また、\(y\)軸での0から最大値(または最小値)までの距離が振幅である点も同じです。ただ横軸は距離ではなく時間であるため、波の上下1セットは波長ではなく、周期になります。
1回振動するために必要な時間が周期です。言い換えると、\(y-t\)グラフで波が上下に1回振動する時間が周期になります。
横軸の単位が異なるため、\(y-x\)グラフと\(y-t\)グラフは異なるグラフです。そこで、\(y-x\)グラフと\(y-t\)グラフで横軸が何を表しているのか理解しましょう。
周期\(T\)と振動数\(f\)の公式
それでは次に、周期\(T\)と振動数\(f\)の公式を確認しましょう。先ほど、周期について学びました。波が上下に1回振動するために必要な時間が周期\(T\)です。一方、1秒間に何回振動するのかを表す指標に振動数\(f\)があります。振動数の単位はHz(ヘルツ)です。
例えば周期が0.5秒の場合、振動数はいくらでしょうか。0.5秒で1回振動するため、1秒では2回振動するとわかります。それに対して周期が0.2秒の場合はどうでしょうか。0.2秒で1回振動するため、1秒では5回振動するとわかります。
このように、周期\(T\)と振動数\(f\)は反比例の関係にあるとわかります。周期(\(y-t\)グラフでの横軸の幅)が短いと、当然ながら1秒間にたくさん振動できます。
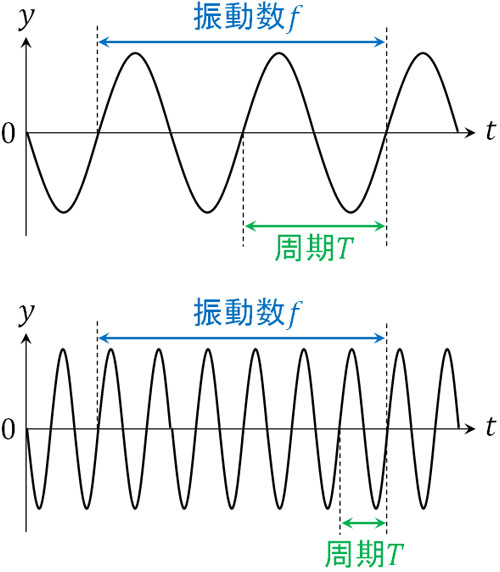
そのため、周期\(T\)と振動数\(f\)には以下の関係があります。
- \(T=\displaystyle\frac{1}{f}\)
もちろん、\(f=\displaystyle\frac{1}{T}\)と変形してもいいです。波を学ぶとき、この公式を覚える必要があります。ただ公式を覚えなくても、周期\(T\)と振動数\(f\)の定義を学べば、この公式が成り立つことを理解できますし、反比例の関係にあることを知っていれば公式を作ることができます。
波の速さ\(v\)、波長\(λ\)、周期\(T\)、振動数\(f\)の関係
ここまでの内容を学べば、波の速さを計算できます。波が来ても横に移動することはありません。ただ波によって、どれだけの速さ\(v\)で伝わるのかに違いがあります。
例えば音の速度は340m/sです。それに対して、海外に打ち寄せる波の速度は音波に比べて非常に遅いです。波には速さがあるのです。このとき、波の速さ\(v\)を表す公式が以下になります。
- \(v=fλ\)
ただこの公式を覚える意味はありません。理由としては、周期\(T\)と振動数\(f\)の関係を表す公式と同様に、この公式が成り立つのは当たり前だからです。
先ほど、1秒間に振動する回数が振動数\(f\)であると解説しました。また、波が上下に揺れるとき、1セットの長さが波長\(λ\)です。
例えば振動数が2Hzの場合、1秒間に2回、上下に波が揺れます。言い換えると、1秒間で2λm/s進みます。また振動数が5Hzの場合、1秒間に5回、上下に波が揺れます。そのため、1秒間で5λm/s進みます。
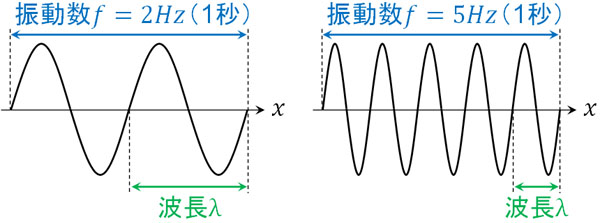
波の性質を理解すれば、なぜ\(v=fλ\)が成り立つのかわかります。また公式を覚える必要はなく、波の性質を学ぶことで\(v=fλ\)をいつでも作ることができます。
また先ほど説明した通り、\(f=\displaystyle\frac{1}{T}\)です。そこで、\(f=\displaystyle\frac{1}{T}\)を\(v=fλ\)に代入しましょう。そうすると、以下の式を得ることができます。
- \(v=\displaystyle\frac{λ}{T}\)
こうして、物理で波の計算問題を解くために必要な3つの公式を導き出すことができました。
- \(T=\displaystyle\frac{1}{f}\)または\(f=\displaystyle\frac{1}{T}\)
- \(v=fλ\)
- \(v=\displaystyle\frac{λ}{T}\)
ただこれまで説明した通り、これらの公式を暗記するのではなく、波の性質を学びましょう。そうすれば、なぜこれらの公式が成り立つのかわかります。
\(y\)軸の高さを表す波の式:sinθまたはcosθを用いて表す
先ほど、横軸に着目して3つの公式を導き出しました。次はたて軸(\(y\)軸)に着目しましょう。一つの点に着目するとき、波は横に移動することはないものの、時間経過と共に上下に動きます。また、同じ振幅で上下に動くため、単振動と捉えることができます。
力学では、単振動を式で表すとき、等速円運動を横から見る必要があります。たて軸だけに着目するとき、波の上下運動は単振動と同じ動きになるため、同様に波を横から確認しましょう。
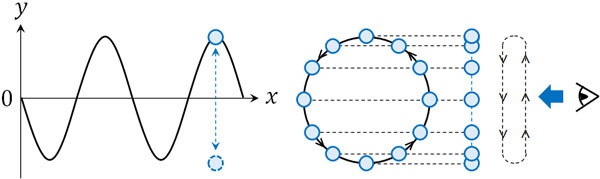
等速円運動とsinθ(またはcosθ)を利用することにより、単振動での上下の動きを式で表すことができるのです。そこで、等速円運動とsinθ(またはcosθ)を利用することで、波の高さを表す式を作りましょう。
先ほどの波であれば、わずかな時間が経過すると、\(y-x\)グラフは以下のように変化します。
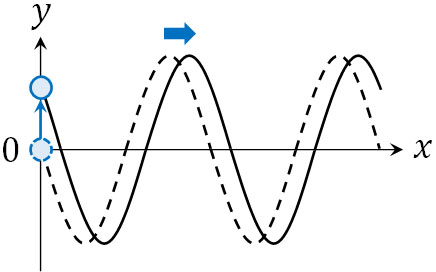
物理では、あなたの頭の中で現象が起こっている場面を想像することが重要です。このように確認すると、\(y\)軸の値は0から増加していくとわかります。そこで振幅を\(A\)、角速度(角振動数)をωとすると、たて軸を表す式は\(y=Asinωt\)となります。
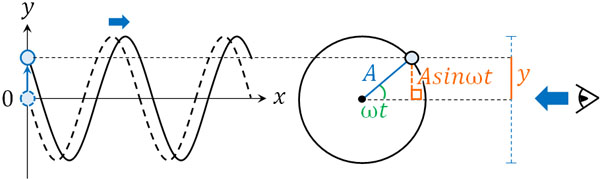
こうして、単振動の変位(変化した距離)を得る公式とまったく同じ式を作ることができます。なお単振動では\(x=Asinωt\)であるものの、波では\(y\)軸を利用するため、\(x\)を\(y\)に変えて\(y=Asinωt\)にしましょう。
また等速円運動や単振動で既に学んだ通り、以下の式が成り立ちます。
- \(ωT=2π\)
周期\(T\)は前述の通り、波が上下に1セット振動する時間を表します。言い換えると、等速円運動で一周するための時間を表します。また円を一周する場合、角度は必ず2π(360°)になります。
なお1秒間で進む角度が角速度ωであるため、角速度ωと周期\(T\)をかけると、必ず2π(360°)になります。そのため、\(ωT=2π\)です。そこで、\(ωT=2π\)を以下のように変形しましょう。
\(ωT=2π\)
\(ω=\displaystyle\frac{2π}{T}\)
そこで、\(ω=\displaystyle\frac{2π}{T}\)を\(y=Asinωt\)に代入します。
\(y=Asinωt\)
\(y=Asin\displaystyle\frac{2π}{T}t\)
こうして、\(y\)軸を表す式は\(y=Asin\displaystyle\frac{2π}{T}t\)とわかりました。
この式を理解するため、\(t\)に0、\(\displaystyle\frac{T}{4}\)、\(\displaystyle\frac{T}{2}\)、\(\displaystyle\frac{3T}{4}\)、\(T\)を代入しましょう。以下のようになります。
- \(t=0\)の場合:\(y=Asin0=0\)
- \(t=\displaystyle\frac{T}{4}\)の場合:\(y=Asin\displaystyle\frac{π}{2}=A\)
- \(t=\displaystyle\frac{T}{2}\)の場合:\(y=Asinπ=0\)
- \(t=\displaystyle\frac{3T}{4}\)の場合:\(y=Asin\displaystyle\frac{3π}{2}=-A\)
- \(t=T\)の場合:\(y=Asin2π=0\)
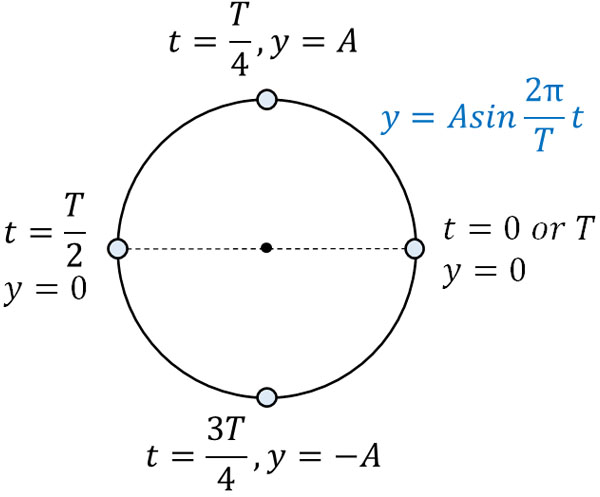
このように確認すると、時間\(t\)が経過することにより、波は\(y\)軸方向で単振動していることがわかります。
出発点が異なると波の式は異なる
なお物理の教科書には、\(y=Asin\displaystyle\frac{2π}{T}t\)が公式として記されていることが多いです。ただ、この公式を覚えても物理の問題を解くことは確実に無理なので、この公式を覚えてはいけません。そうではなく、波の性質を理解して公式を作れるようになりましょう。
単振動では、公式が役に立ちません。波のたて軸は単振動であるため、同様に公式を覚えても役に立たないのです。
例えば以下のグラフで振幅が\(A\)のとき、時間経過による\(y\)軸の変化を表す式はどのようになるでしょうか。
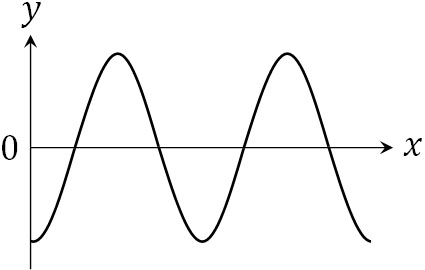
\(t=0\)のとき、\(y\)は最小値になります。\(t=0\)というのは、等速円運動で角度が0を意味します。角度が0のとき、最大値や最小値になるためには、sinθではなくcosθを利用しなければいけません。\(cos0=1\)であり、\(-cos0=-1\)だからです。
なおグラフより、スタート地点は\(y\)軸の最小値です。またわずかな時間が経過すると、\(y\)の値は増えます。
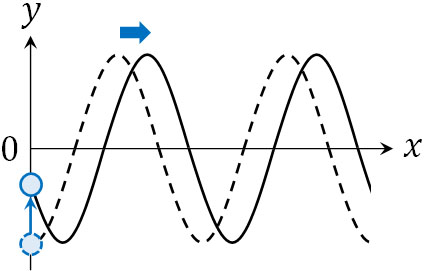
この条件を満たす必要があるため、\(-cosθ\)を利用しましょう。\(-cos0=-1\)であり、角度が大きくなるに従って値は大きくなります。そのため振幅が\(A\)の場合、\(y\)軸を表す波の式は以下のようになります。
- \(y=-Acos\displaystyle\frac{2π}{T}t\)
波の式を作るとき、\(t=0\)のときのスタート地点によって式が変わります。これが、公式を覚えても役に立たない理由です。そこで、波の式を作れるようになりましょう。
グラフと波の式に関する練習問題
それでは、実際に問題を解いてみましょう。以下の問題の答えは何でしょうか。
- \(x\)軸に正の向きで進んでいる波があります。下図について、\(t=0\)のときの様子を表しているのが\(y-x\)グラフであり、\(y-t\)グラフは特定の位置\(x\)での単振動を表しています。

- この波の振幅\(A\)、波長\(λ\)、周期\(T\)、振動数\(f\)、速さ\(v\)を求めましょう。
- \(t=0\)を基準とするとき、\(y\)軸の高さを表す波の式を求めましょう。
- \(t=0\)のとき、波の速度が鉛直上向き(\(y\)軸の正の向き)で最大になる位置と速さと求めましょう。
- \(t=0\)のとき、波の加速度が鉛直上向き(\(y\)軸の正の向き)で最大になる位置と加速度の大きさと求めましょう。
1) この波の振幅\(A\)、波長\(λ\)、周期\(T\)、振動数\(f\)、速さ\(v\)を求めましょう
図より、以下のようになります。
- 振幅\(A\):1m
- 波長\(λ\):8m
- 周期\(T\):2s
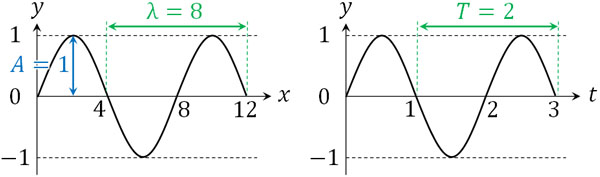
また、振動数\(f\)は\(f=\displaystyle\frac{1}{2}=0.5\)Hzです。速さ\(v\)は\(v=8×0.5=4\)m/sです。
2) \(t=0\)を基準とするとき、\(y\)軸の高さを表す波の式を求めましょう
スタート地点の\(y\)の位置は0であるため、sinθを利用して式を作ればいいとわかります。また以下のように、少し時間が経過すると\(y\)の値はマイナスになります。
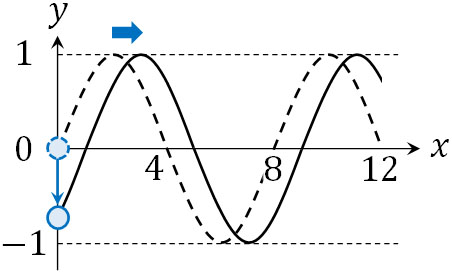
時間経過によって\(y\)の値が低くなるようにするため、波の式にはマイナスを加えましょう。また\(A=1\)であり、\(T=2\)であるため、以下の式になります。
\(y=-sin\displaystyle\frac{2π}{2}t\)
\(y=-sinπt\)
こうして、式は\(y=-sinπt\)になるとわかります。
3) \(t=0\)のとき、波の速度が鉛直上向き(\(y\)軸の正の向き)で最大になる位置と速さと求めましょう
前述の通り、\(y\)軸の波の動きは単振動と同じです。そのため、等速円運動を利用して単振動の速度を計算するのと同じ方法によって、波の速度を求めましょう。
単振動を学んでいるのであれば、振動の中心(\(y=0\))で速度が最大になるとわかります。それでは、\(y\)軸の正の向きなのは\(x=4\)(や\(x=12\))の位置でしょうか。それとも、\(x=8\)の位置でしょうか。
正解を得るため、少し時間が経過した図を作りましょう。少し時間が経過した場合、\(x=4\)や\(x=12\)の位置では、点が上に移動しています。それに対して、\(x=8\)の位置では点が下に移動しています。
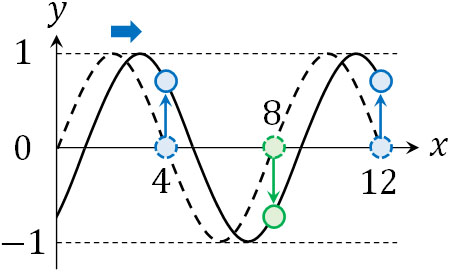
つまり、\(y\)軸の正の向きに移動しているのは\(x=4\)と\(x=12\)です。なお単振動で速さの最大値というのは、円運動での速さと一致します。
等速円運動の公式より、\(v=rω\)です。また先ほど説明した通り、\(ωT=2π\)となるため、\(ω=\displaystyle\frac{2π}{T}\)です。つまり、\(v=r\displaystyle\frac{2π}{T}\)です。そこで、\(v=r\displaystyle\frac{2π}{T}\)に値を代入しましょう。
\(v=1×\displaystyle\frac{2π}{2}\)
\(v=π\)
こうして、波の速度が\(y\)軸の正の向きで最大になる位置は図の\(x=4\)と\(x=12\)であり、速さはπm/sとわかりました。
4) \(t=0\)のとき、波の加速度が鉛直上向き(\(y\)軸の正の向き)で最大になる位置と加速度の大きさと求めましょう
速さの計算ができるようになれば、加速度の計算も容易です。\(y\)の値が最大になるとき、加速度も最大になります。つまり\(x=2,10\)または\(x=6\)のとき、加速度が\(y\)軸の正の向きで最大になります。そこで、以下の図を作りましょう。
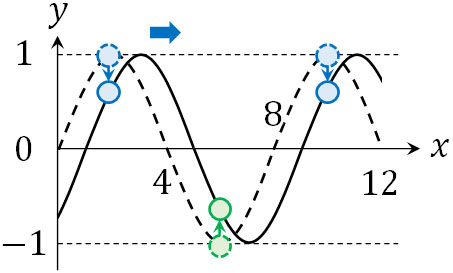
こうして、\(x=6\)のときに\(y\)軸の正の向きで加速度が最大になるとわかります。
単振動で加速度が最大になるとき、等速円運動の加速度と一致します。等速円運動の公式より、\(a=rω^2\)です。\(ω=\displaystyle\frac{2π}{T}\)を代入すると、\(a=r\displaystyle\frac{4π^2}{T^2}\)となります。そこで、式に値を代入しましょう。
\(a=r\displaystyle\frac{4π^2}{T^2}\)
\(a=1×\displaystyle\frac{4π^2}{2^2}\)
\(a=π^2\)
こうして、波の加速度が\(y\)軸の正の向きで最大になる位置は図の\(x=6\)であり、加速度はπ2m/s2とわかりました。
横波と縦波
なおこれまでの説明では、波は横に動かないと解説しました。ただ実際には、この説明は間違っています。波はたてに動くことがあれば、横に動くこともあります。
これまで説明した波は横波に該当します。ただ、波には横波だけでなく縦波もあります。横波でも縦波でも、波の基本的な性質は同じです。
縦波はイメージしにくいかもしれません。縦波を理解するとき、ばねを押したり引いたりする場面を想像しましょう。この場合、ばねには密集している部分と広がっている部分が作られます。
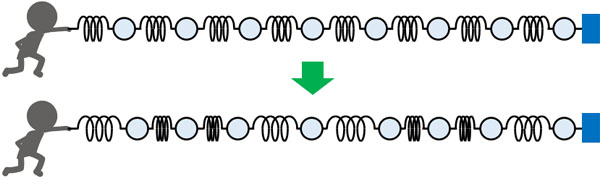
密集と拡散を繰り返すのが縦波です。そのため、縦波は疎密波とも呼ばれています。
縦波のままでは理解しにくいため、グラフにするときは縦波を横波に変えます。例えば、自然長と比べて\(x\)軸の正の位置にある場合、\(y\)軸で正にしましょう。また負の位置にある場合、\(y\)軸で負にします。この場合、以下の図を作ることができます。
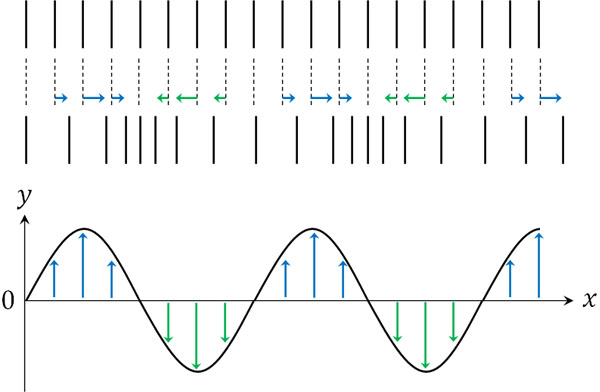
図を確認すると、縦波に特徴的なポイントがわかります。横波では、\(y=0\)のときに速さが最大になります。
一方で縦波では、\(y=0\)のときに速さがありません。右にも左にも動いていないのです。また右にも左にも動いていないからこそ、\(y=0\)となるのです。そのため縦波では、\(y\)の値が最大または最小のとき、最も速くなります。
また図より、最も密な点または最も疎な点は\(y=0\)となる場所です。縦波はイメージしにくいものの、横波の図を作ることで理解しましょう。
波の性質を学び、公式を利用できるようにする
私たちが生活をするうえで波は欠かせません。光や音は波ですし、電波がなければ機器類は機能しません。物理で波動を学ぶのは、これらの仕組みを理解するために必要なのです。
そこで、波の性質を学びましょう。\(y-x\)グラフと\(y-t\)グラフを利用し、振幅や波長、周期を計算できるようにするのです。また周期と振動数の関係を理解し、どのように計算すれば波の速さを得られるのか学びましょう。
なお\(y\)軸方向の波の式を作るとき、等速円運動を理解しておく必要があります。単振動と波の式は同じであり、円運動を利用することによって式を作れるようになります。また、速度や加速度の計算も可能になります。
ただ横波だけでなく、縦波も存在します。横波と縦波の違いを確認し、縦波を横波のグラフで描けるようにしましょう。これらが波動の基本的な内容です。






