等温変化・断熱変化：公式やP-Vグラフの変化、ポアソンの法則

熱力学で学ぶ気体の状態変化には、等温変化と断熱変化があります。温度が一定の場合は等温変化であり、外部との熱のやり取りがない場合は断熱変化です。

等温変化と断熱変化の区別が難しいと考える人は多いです。ただ両者はまったく異なるため、等温変化と断熱変化を見分けられるようにしましょう。等温変化と断熱変化では\(P-V\)グラフの形が似ているものの、性質は異なります。

なお断熱変化で成り立つ法則にポアソンの法則があります。ポアソンの法則を利用する場面は少ないものの、どのような法則なのか事前に理解しておきましょう。

それでは、等温変化と断熱変化ではどのように気体の状態変化が起こるのでしょうか。等温変化と断熱変化の特徴を解説していきます。

1 等温変化では内部エネルギーの変化がゼロになる
- 1.1 \(P-V\)グラフと等温変化の関係
2 断熱変化では熱量\(Q\)がゼロになる
3 等温変化と断熱変化の違いを知る

等温変化では内部エネルギーの変化がゼロになる

等温変化では、容器内の気体の温度が常に一定です。加える熱量\(Q\)がゼロになるわけではなく、温度が常に同じです。温度が同じであっても、熱量を与えることは可能です。なお等温変化では、温度が一定になるので温度変化\(ΔT\)がゼロになります。

内部エネルギーの変化は以下の公式によって得ることができます。

\(ΔU=\displaystyle\frac{3}{2}nRΔT\)

等温変化だと\(ΔT=0\)であるため、\(ΔU=0\)です。つまり等温変化では、内部エネルギーの変化はありません。また熱力学第一法則より、\(Q=ΔU+W\)です。そのため、等温変化では公式を以下のように変形できます。

\(Q=W\)

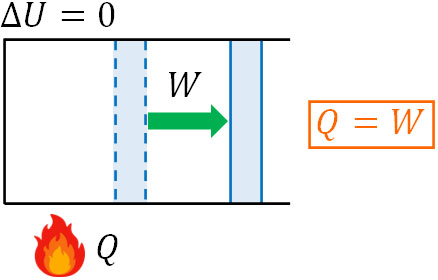
気体による等温変化では、加えた熱量はすべて仕事に利用されます。熱量を与えると気体が膨張することで体積が増えますし、熱量を取り去ると気体の体積が減ることで仕事の値はマイナスになるのです。

\(P-V\)グラフと等温変化の関係

それでは、等温変化だと\(P-V\)グラフの形はどのようになるのでしょうか。気体の状態方程式より、以下の式が成り立ちます。

\(PV=nRT\)

等温変化では温度\(T\)が一定です。そのため\(nRT\)の値は変化がなく、定数と考えることができます。そこで、\(nRT=a\)としましょう。そうすると、式は以下のようになります。

\(PV=a\)

つまり、圧力\(P\)と体積\(V\)をかけると常に一定の値となります。

\(PV=\)一定

それでは、先ほどの式を以下のように変形しましょう。

\(P=\displaystyle\frac{a}{V}\)

つまり等温変化では、圧力\(P\)と体積\(V\)は反比例の関係にあるとわかります。圧力\(P\)が上昇すれば、体積\(V\)は小さくなります。一方、圧力\(P\)が小さくなれば、体積\(V\)は大きくなります。

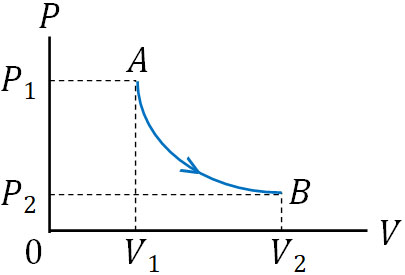
例えば温度を一定にして、以下のようにピストンをゆっくり引く場合はどのようになるでしょうか。気体の体積は増えており、気体は外部へ仕事をすることになります。ただ、容器内の圧力は減少します。

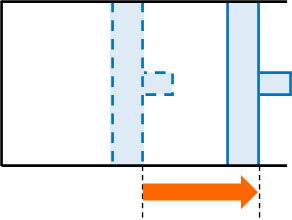
室温環境下（等温変化）でシリンダーのピストンを引いた後、手を離すとピストンは元の位置へ戻るのは容易に想像できます。これは、容器内の圧力が減少しているからです。手を離すと大気圧によって押され、結果としてピストンは元の位置へ移動します。

また、シリンダーのピストンを押すと逆の現象が起こります。ピストンを押すと容器内の圧力が上昇し、体積が減るのは容易に理解できます。この関係を数式で表すと\(P=\displaystyle\frac{a}{V}\)になるのです。

断熱変化では熱量\(Q\)がゼロになる

気体の状態変化で重要な内容に断熱変化があります。等温変化では、温度\(T\)が一定であり、熱量\(Q\)は変化します。一方、断熱変化では熱量\(Q\)（熱の出入り）がゼロであるものの、温度\(T\)は変化します。

容器に対して断熱材を使用する場合、熱量の出入りはないと考えます。この場合、断熱変化になります。つまり断熱変化とは、容器内の気体に対して熱を与えない変化（または、容器内の気体から熱を奪わない変化）と理解しましょう。

そのため熱力学第一法則を利用すると、以下の関係が成り立ちます。

\(0=ΔU+W\)

\(ΔU=-W\)

式を確認すると、内部エネルギーと仕事で符号が逆になっているとわかります。そのため断熱変化では、気体が外に仕事をするとき（気体の体積が増えるとき）、内部エネルギーが減少します。内部エネルギー変化\(ΔU\)は温度変化\(ΔT\)を意味しているため、気体の体積が増えると温度が低下します。

シリンダーのピストンを速いスピードで引くと、容器内の温度は非常に低くなることが知られています。これは、気体が外部へ仕事をすることにより（気体の体積が増えることにより）、内部エネルギー（温度）が低下するからです。

反対にピストンを速いスピードで押すと、容器内の温度は高くなります。気体の体積が減ることによって内部エネルギー（温度）が上昇するのです。

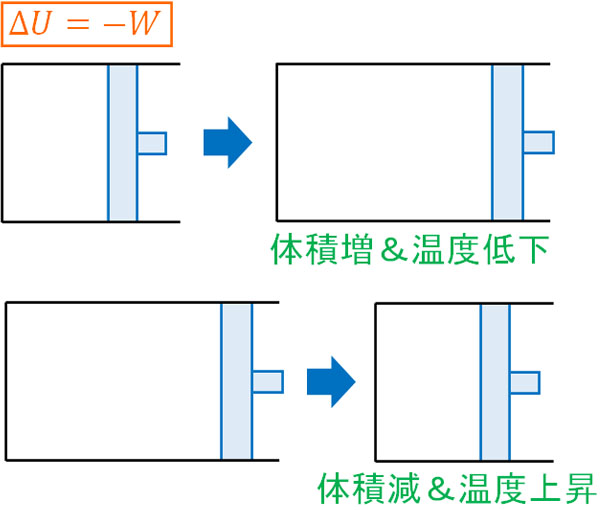
断熱変化というのは、温度変化のない変化ではありません。温度が変化しないのは等温変化です。断熱変化では外部とのエネルギーのやり取りがないものの、温度変化はするのです。

断熱変化での\(P-V\)グラフと等温変化との違い

次に、断熱変化での\(P-V\)グラフの形を学びましょう。\(P-V\)グラフを確認すると、断熱変化と等温変化は似ています。断熱変化では、以下のような\(P-V\)グラフになります。

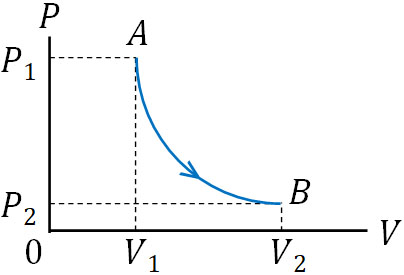
等温変化に比べると、断熱変化のほうがグラフの傾きが急になります。なぜ、等温変化よりも断熱変化でグラフの傾きが急になるのでしょうか。この理由として、断熱変化では温度変化があるからです。

断熱変化では、体積が大きくなることによって温度が下がります。例えば350Kの等温変化の曲線と300Kの等温変化の曲線がある場合、体積が\(V_1\)から\(V_2\)へ増えることで350Kから300Kへ温度が変化したのであれば、以下のような\(P-V\)グラフとなります。

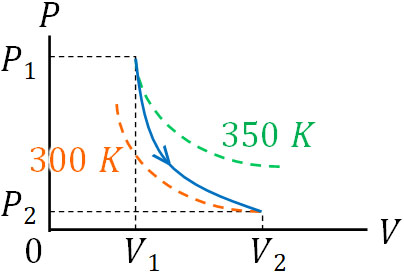
断熱変化では、「等温変化での異なる曲線」を結ぶことになります。そのため、必然的に等温変化よりも傾きが急になるのです。断熱変化の\(P-V\)グラフは理解しにくいです。そこで、「等温変化のグラフ（反比例のグラフ）に対して、温度変化が加わると断熱変化のグラフになる」と理解しましょう。

なお先ほどのグラフについて、体積が同じ場合（例えば体積が\(V_1\)）で比較すると、温度が高いほど当然ながら圧力は大きくなります。そのため等温変化のグラフを描くとき、高い温度の曲線を上、低い温度の曲線を下に描きましょう。

\(P-V\)グラフを利用する練習問題

ここまでの内容を理解して、練習問題を解いてみましょう。以下の問題の答えは何でしょうか。

断熱容器内になめらかに動くピントンがあり、理想気体の単原子分子を入れた後、ピストンを押して気体を圧縮しました（断熱変化）。次に熱の出入りが可能な容器に変え、気体の温度を一定にして、先ほどと同じ距離だけピストンを押しました（等温変化）。圧力変化が大きいのは、断熱変化と等温変化のうちどちらでしょうか。

まず、\(P-V\)グラフを作りましょう。ピストンを押す距離は同じであるため、気体の体積減少\(ΔV\)の値は同じです。

断熱変化では、ピストンを押すことで気体の体積が減少すると、容器内の温度（内部エネルギー）が高くなります。一方で等温変化の場合、気体の体積が減少することで圧力は高くなるものの、容器内の温度は同じです。そのため、以下の\(P-V\)グラフを作ることができます。

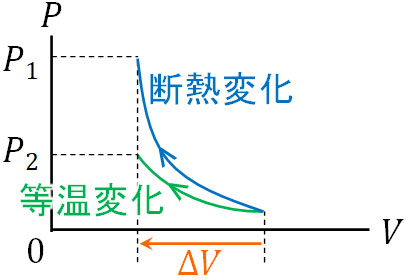
出発点（圧力と体積）は同じです。ただ、体積が減少した後の圧力は断熱変化と等温変化で異なります。断熱変化では体積減少によって温度が高くなるため、より圧力が上昇します。

そこで体積が減少した後の\(P-V\)グラフを確認すると、断熱変化での圧力\(P_1\)と等温変化での圧力\(P_2\)では、断熱変化での圧力\(P_1\)のほうが高いです。そのため、圧力変化が大きいのは断熱変化と判断できます。

ポアソンの法則：断熱変化で成り立つ法則

なお断熱変化ではポアソンの法則を利用できます。そこまで重要ではない法則であるものの、断熱変化を学ぶ場合は理解しましょう。

ポアソンの法則の導出は複雑であり、積分も利用する必要があるため、結果のみを記します。ポアソンの法則では、圧力\(P\)と体積\(V\)について以下の関係が成り立ちます。

\(PV^γ=\)一定

なお、\(γ=\displaystyle\frac{C_P}{C_V}\)であり、\(C_P\)は定圧モル比熱、\(C_V\)は定積モル比熱を表します。

また理想気体の単原子分子では、\(C_P=\displaystyle\frac{5}{2}R\)、\(C_V=\displaystyle\frac{3}{2}R\)です。そのため、\(γ=\displaystyle\frac{C_P}{C_V}=\displaystyle\frac{5}{3}\)です。つまり理想気体の単原子分子では、ポアソンの法則は以下のようになります。