物体を水平方向または鉛直方向へ移動させるとき、物理では「仕事をした」と表現します。力を加えることによって、どれだけのエネルギーを与えたのかによって仕事の大きさが変化します。
このとき重要な概念が運動エネルギーや位置エネルギー、弾性エネルギーです。物体はエネルギーをもっているのです。例えば、高速で動いている物体を手で受け止めると痛いです。これは、スピードの速い物体であるほどエネルギーが高いからです。
そこで速さや高さ、ばねの弾性力がもつエネルギーを利用して、物体がもつエネルギーを計算しましょう。また運動の前後でどれだけエネルギーが変化しているのかを計算するとき、力学的エネルギー保存則が役立ちます。
物体がもつエネルギーに着目することによって、移動距離や速さなどを計算できます。そこで、仕事とエネルギーの関係や計算方法、公式の意味を解説していきます。
もくじ
物理での仕事とは何か:仕事の公式とジュール(J)
まず、「物理で学ぶ仕事」とは何かを理解しましょう。重い物体を運ぶとき、1m運ぶのと5m運ぶのでは、当然ながら5m運ぶほうがあなたは5倍疲れます。言い換えると、あなたはエネルギーを消費することで5倍の仕事をしなければいけません。
つまりエネルギーを与えて仕事をするためには、与える力に加えて、移動距離が重要であるとわかります。仕事(仕事量)を\(W\)、力を\(F\)、移動距離を\(x\)とすると、以下の公式によって仕事を計算できます。
- \(W=F×x\)
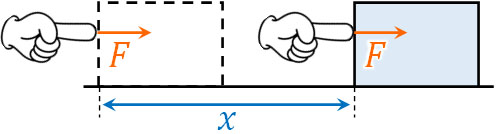
仕事とは何かを理解すれば、この公式を覚えるのは難しくありません。力を加えるとき、移動距離が長いほど仕事量が多いのは当然です。そこで、力と移動距離のかけ算によって仕事を計算しましょう。
なお、仕事の単位はジュール(J)です。ニュートン(N)とメートル(m)をかけることによってジュール(J)を得ることができます。
つり上げや斜面移動での仕事と仕事率:垂直方向では仕事に関与しない
なおつり上げや斜面移動であっても仕事の大きさを計算できます。ただ仕事の計算をするとき、力の向きと移動の向きが同じでなければいけません。そのため移動の向きに対して、垂直方向の力を加えても仕事に関与しません。
例えば床に置かれている物体を移動させるとき、垂直抗力が物体に加えた力はいくらになるでしょうか。物体の移動と垂直抗力は垂直関係にあるため、垂直抗力が物体に与えるエネルギーはゼロです。
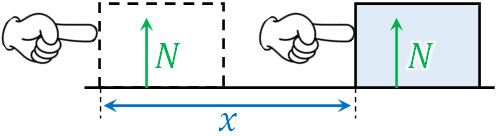
一方、物体が床に置かれているとき、摩擦力は仕事の大きさに関与しています。例えば移動距離は同じであっても、動摩擦力が大きくなるほど仕事の大きさは増えます。このように、移動と力の方向は一致している必要があるのです。
移動と力の方向が一致していれば、つり上げや斜面移動であっても仕事をしたことになります。例えば斜面に置かれた物体に糸をつけ、張力\(T\)によって距離\(x\)を移動させる場合、仕事の大きさは\(W=Tx\)です。
また物体に糸をつけ、張力\(T=mg\)によって高さ\(h\)の距離を持ち上げれば、\(W=Th=mgh\)の仕事をしたことになります。
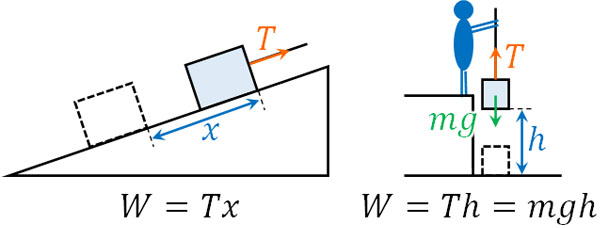
物体の移動と力の方向を一致させ、かけることによって仕事の大きさを得られることを理解しましょう。
・1秒あたりにどれだけの仕事をしたのか表す仕事率
なお、1秒あたりにどれだけの仕事をしたのか表す指標に仕事率があります。計算方法は簡単であり、仕事(J)に対してかかった時間で割るだけです。例えば20秒の時間をかけて100Jの仕事を行った場合、仕事率は20J/sです。
仕事と仕事率に関する練習問題
それでは、実際に問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 荒い床に物体を置き、糸をつけて地面との角度がθとなるように糸を引っ張りました。なお、糸の張力は\(T\)、移動距離は\(x\)、動摩擦係数は\(μ’\)です。
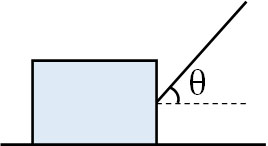
- 「糸の張力」「重力」「垂直抗力」「摩擦」について、それぞれした仕事を求めましょう。
- 距離\(x\)を移動させるのに10秒かかった場合、糸の張力による仕事率はいくらでしょうか。
1) 「糸の張力」「重力」「垂直抗力」「摩擦」について、それぞれした仕事を求めましょう
重力と垂直抗力については、物体の移動方向に対して垂直です。そのため、重力と垂直抗力による仕事は0です。そこで糸の張力と摩擦について、それぞれ仕事を計算しましょう。
糸の張力と摩擦を図に記入すると以下のようになります。
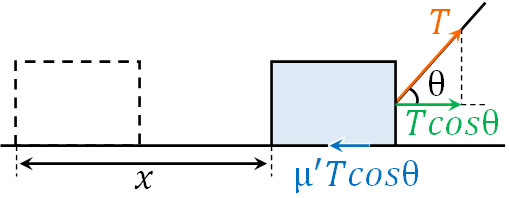
そのため、以下のように仕事を計算できます。
- 糸の張力:\(Tcosθ·x\)
- 摩擦:\(-μ’Tcosθ·x\)
力の向き(糸を引っ張っている向き)を正とする場合、動摩擦力は反対向きに働いています。そのため、摩擦による仕事はマイナスになります。
2) 距離\(x\)を移動させるのに10秒かかった場合、糸の張力の仕事率はいくらでしょうか
先ほどの答えに対して、かかった時間(10秒)で割りましょう。そうすると、仕事率は\(\displaystyle\frac{T’cosθ·x}{10}\)であるとわかります。
運動エネルギー・位置エネルギー・弾性エネルギーの関係
物理での仕事の概念を理解したら、仕事とエネルギーの関係を学ぶことができます。エネルギーを与えることによって、仕事をすることができるからです。
力学で取り扱うエネルギーには主に3種類あります。公式と共に記すと、以下の3種類になります。
- 運動エネルギー:\(\displaystyle\frac{1}{2}mv^2\)
- 位置エネルギー:\(mgh\)
- 弾性エネルギー:\(\displaystyle\frac{1}{2}kx^2\)
速度のある物体はエネルギーをもっています。前述の通り、速いスピードで動いている物体であるほど、あなたが手で受け止めるときの衝撃が大きいです。このとき物体の質量\(m\)と速度\(v\)を利用し、\(\displaystyle\frac{1}{2}mv^2\)で運動エネルギーを表すことができます。
また速度がゼロであっても、高い場所に物体がある場合、物体はエネルギーをもちます。高い場所にある物体がもつエネルギーが位置エネルギーです。事実、高いところから物体を落とすと大きな衝撃となります。位置エネルギーは質量\(m\)、重力加速度\(g\)、高さ\(h\)を利用して、\(mgh\)で表すことができます。
ばねについても、自然長からのズレが大きくなるほどエネルギーをもちます。弾性エネルギーはばね定数\(k\)とばねが伸びている距離(または縮んでいる距離)\(x\)を利用し。\(\displaystyle\frac{1}{2}kx^2\)で表すことができます。
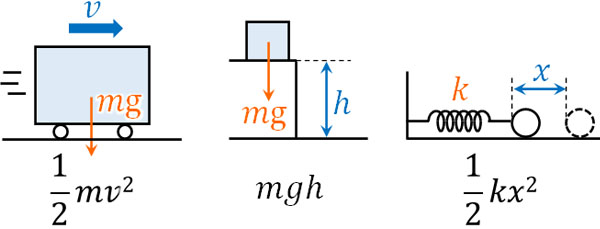
運動エネルギーや位置エネルギー、弾性エネルギーを得るとき、先ほど解説した公式に値を代入することで計算できます。
なぜ運動エネルギーの公式を得られるのか
それでは、なぜ運動エネルギーの公式は\(\displaystyle\frac{1}{2}mv^2\)なのでしょうか。位置エネルギーの公式は理解しやすいです。物体に加わる重力は\(mg\)であるため、高さ\(h\)を持ち上げるために必要な仕事は\(W=mgh\)です。鉛直上向きの仕事の計算方法は先ほど説明した通りです。
一方、運動エネルギーを計算するときは速度\(v\)を利用します。運動エネルギーをもつ物体というのは、静止している状態(初速度\(v_0=0\))から、速度\(v\)になっていることを意味します。そこで、等加速度直線運動の公式を利用して運動エネルギーの公式を導き出しましょう。
利用する等加速度直線運動の公式は以下になります。
- \(v^2-v_0^2=2ax\)
初速度は0であり、以下のように加速度\(a\)の式に変換しましょう。
\(v^2-v_0^2=2ax\)
\(v^2-0=2ax\)
\(a=\displaystyle\frac{v^2}{2x}\)
常に一定の力を物体に加えているというのは、言い換えると「常に一定の加速度を物体に加えている」ことを意味します。\(F=ma\)であり、物体の重さは変化しないため、力の大きさが同じ場合、物体は加速度を得ることによって一定の割合で徐々に速くなるのです。そのため、等加速度直線運動の公式を利用できます。
なおこれまで説明した通り、仕事の定義は\(W=F×x\)です。また\(F=ma\)であるため、以下のように仕事の式を変形できます。
\(W=F×x\)
\(W=ma×x\)
そこで、\(a=\displaystyle\frac{v^2}{2x}\)を\(W=ma×x\)に代入しましょう。
\(W=ma×x\)
\(W=\displaystyle\frac{mv^2}{2x}×x\)
\(W=\displaystyle\frac{1}{2}mv^2\)
こうして、静止している状態から速度\(v\)の状態にするためには、\(W=\displaystyle\frac{1}{2}mv^2\)のエネルギーを与えなければいけないことがわかります。言い換えると、速度\(v\)で動いている物体のエネルギーの大きさは\(\displaystyle\frac{1}{2}mv^2\)です。
このように仕事の定義と等加速度直線運動の公式を利用することにより、運動エネルギーの公式を導き出せます。
なお、ばねの弾性エネルギーも同じ方法によって公式を導き出すことができます。\(F=kx\)であるため、運動エネルギーの質量\(m\)をばね定数\(k\)に変え、速度\(v\)をばねの伸び\(x\)に変えて計算すると、ばねのエネルギー\(\displaystyle\frac{1}{2}kx^2\)を得ることができます。
運動エネルギー(位置エネルギー)の変化が仕事
力を加えることによって物体に速度を加えたり、持ち上げたりすることにより、物体はエネルギーをもつようになります。つまり、物体がもつ運動エネルギーや位置エネルギーの変化を確認すると、仕事の大きさがわかります。
例えば、以下の問題の答えは何でしょうか。
- 質量\(m\)、速度\(v\)の物体に力を加え、速度\(2v\)になったとします。このとき、加えたエネルギー(仕事の大きさ)はいくらでしょうか。

仕事をすることによってスピードが上昇している(エネルギーが大きくなっている)ため、仕事の大きさは正です。またすべての計算で共通しますが、後の結果から前の結果を引くことによって変化量を計算できます。そこで、以下のように仕事を計算しましょう。
\(\displaystyle\frac{1}{2}m(2v)^2-\displaystyle\frac{1}{2}mv^2\)
\(=\displaystyle\frac{3}{2}mv^2\)
こうして、仕事の大きさ(加えられたエネルギー)は\(\displaystyle\frac{3}{2}mv^2\)と計算できます。なお位置エネルギーについても同様の方法で計算可能です。例えば、以下の問題の答えは何でしょうか。
- 質量\(m\)の物体が高さ\(h\)の位置にあります。物体が高さ0の場所へ落ちて静止しているとき、行われた仕事の大きさはいくらですか。なお、重力加速度は\(g\)です。
物体が高さ\(h\)の位置にある場合、位置エネルギーは\(mgh\)です。物体を落下させ、高さ0の場所で静止している場合、物体が保有するエネルギーは0です。エネルギーの変化(仕事の大きさ)を計算するため、後の状態から前の状態を引くと以下のようになります。
\(0-mgh=-mgh\)
こうして、仕事の大きさは\(-mgh\)とわかります。仕事が負であるため、物体はエネルギーを放出しているとわかります。
・仕事は加えられたエネルギーである
なおここまでの解説より、物体に対して仕事を行う(エネルギーを加える)ことによって、変化後のエネルギーをもつ物体となります。そのため、以下のように表すこともできます。
- 変化前のエネルギー + 仕事(加えたエネルギー) = 変化後のエネルギー
運動エネルギーや位置エネルギー、弾性エネルギーを理解するため、仕事とエネルギーの関係を把握しましょう。
摩擦による運動エネルギーの減少と摩擦熱
なお物体を荒い床の上で滑らせる場合、摩擦力が働きます。物体に力が加わっていない場合、物体と床との摩擦によって徐々に物体のスピードが減少し、最終的に物体の速度は0になります。言い換えると、摩擦による仕事が行われています。
そこで、摩擦によって運動エネルギーが減少する場面を考えましょう。例えば、以下の問題の答えは何でしょうか。
- 荒い床に質量\(m\)の物体を置き、初速度\(v_0\)で運動させました。この物体が静止するまでに動いた距離\(x\)を求めましょう。なお動摩擦係数は\(μ’\)であり、重力加速度は\(g\)です。
物体に働く力は垂直抗力と摩擦力です。垂直抗力は運動の方向に対して垂直であるため、仕事をしません。そのため、仕事をするのは動摩擦力のみです。
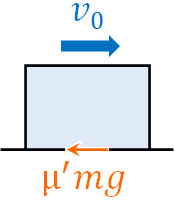
速度\(v_0\)で運動していた物体が速度0になるため、加えられたエネルギーはマイナスです。また動摩擦力は運動方向に対して反対向きに働くため、動摩擦力による仕事はマイナスです。
言い換えると、動摩擦力によってマイナスのエネルギーが加えられるため、物体の速度は徐々に遅くなり、スピードがゼロになります。そこで運動エネルギーの変化(仕事の大きさ)と動摩擦力による仕事を利用し、式を作りましょう。
運動エネルギーの変化と動摩擦力による仕事量は同じです。そのため、計算式は以下になります。
\(0-\displaystyle\frac{1}{2}mv_0^2=-μ’mg·x\)
\(\displaystyle\frac{1}{2}v_0^2=μ’gx\)
\(x=\displaystyle\frac{v_0^2}{2μ’g}\)
こうして、移動距離は\(x=\displaystyle\frac{v_0^2}{2μ’g}\)になるとわかりました。
なお物体をこすると、熱が発生することは多くの人が既に理解していると思います。先ほどの問題では、動摩擦力によって\(-μ’mg·x\)の仕事が行われました。つまり摩擦により、物体から\(μ’mg·x\) Jのエネルギーが失われています。
物体から失われたエネルギーというのは、摩擦の場合は熱として放出されます。これを摩擦熱といいます。
抵抗力に関する力学の練習問題
摩擦力や抵抗力が加わると、物体の速度は遅くなります。次は摩擦力ではなく、抵抗力が加わるときの物体の運動を計算しましょう。以下の問題の答えは何でしょうか。
- 質量M、長さLの木材を置き、この木材に対して重さmの銃弾を速度\(v\)にて水平に撃ち込みます。銃弾が木材から受ける抵抗力は一定であり、木材は固定されています。なお、解答はm、M、L、\(v\)を利用しましょう。
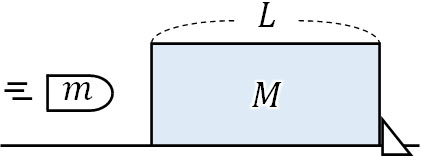
- 銃弾は木材の\(\displaystyle\frac{L}{2}\)の位置で止まりました。銃弾が木材から受ける抵抗力の大きさはいくらですか。
- 銃弾が木材を貫通するために必要な最低の速度\(V\)を求めましょう。
1) 銃弾は木材の\(\displaystyle\frac{L}{2}\)の位置で止まりました。銃弾が木材から受ける抵抗力の大きさはいくらですか
銃弾を撃ち込んだ後、運動エネルギーはゼロになります。木材から逆向きに力が加えられることにより、徐々に銃弾のスピードが落ちていくのです。
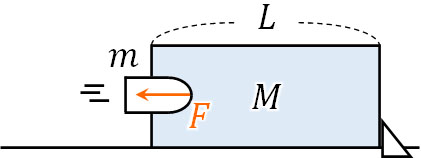
抵抗力を\(F\)とします。移動している向きと反対に力\(F\)が加わり、移動距離は\(\displaystyle\frac{L}{2}\)です。そのため、抵抗力によって行われた仕事は\(W=-F×\displaystyle\frac{L}{2}\)です。
また、銃弾は速度\(v\)から速度0に変化しています。言い換えると、抵抗力によって仕事が行われ、銃弾の速度は0になります。そこで、以下の式を作りましょう。
\(0-\displaystyle\frac{1}{2}mv^2=-F×\displaystyle\frac{L}{2}\)
\(F=\displaystyle\frac{mv^2}{L}\)
こうして、銃弾が受ける抵抗力は\(\displaystyle\frac{mv^2}{L}\)とわかります。
2) 銃弾が木材を貫通するために必要な最低の速度\(V\)を求めましょう
式を作るときの考え方は先ほどと同じです。銃弾が板を貫通するためには、少なくとも距離\(L\)を進まなければいけません。このとき抵抗力によって行われた仕事は\(W=-FL\)です。そのため、以下の計算をしましょう。
\(0-\displaystyle\frac{1}{2}mV^2=-FL\)
\(V^2=\displaystyle\frac{2FL}{m}\)
先ほどの答えより、\(F=\displaystyle\frac{mv^2}{L}\)を代入しましょう。
\(V^2=\displaystyle\frac{2L}{m}×\displaystyle\frac{mv^2}{L}\)
\(V^2=2v^2\)
\(V=\sqrt{2}v\) (\(V>0\))
こうして、板を貫通させるために必要な最低の速度は\(\sqrt{2}v\)と計算できます。
力学的エネルギー保存則:エネルギーの合計は変化しない
なお、すべてのエネルギーを合計すると前後で同じになります。つまり、エネルギーの総和が常に一定であることを理解すれば、物体がもつエネルギーを計算できます。
運動エネルギーや位置エネルギー、弾性エネルギーを総称して力学的エネルギーといいます。力学的エネルギーの総和が常に同じとなる法則を力学的エネルギー保存則といいます。そのため、以下のようになります。
- 運動エネルギー + 位置エネルギー + 弾性エネルギー = 一定
例えば、ばねを利用して物体を加速させる場合、弾性エネルギーが運動エネルギーへ変化します。また速度をもつ物体が坂を上がる場合、スピードが落ちることで運動エネルギーが位置エネルギーへと変化します。
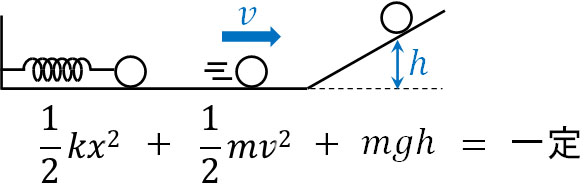
ただエネルギーの中身が変わっても、エネルギーの合計は変化しません。この性質を利用して、物体の速度や移動距離、高さの計算が可能になります。
なお摩擦や抵抗力(空気抵抗など)を考慮する場合、力学的エネルギー保存則は成り立ちません。例えば摩擦力が存在する場合、一部のエネルギーは熱(摩擦熱)として消えるからです。そのため力学的エネルギー保存則を利用するとき、摩擦や抵抗力が存在しないことを確認しましょう。
力学的エネルギー保存則に関する練習問題
それでは、力学的エネルギー保存則を利用して計算問題を解きましょう。以下の問題の答えは何でしょうか。
- 高さ\(h\)の位置から、質量\(m\)のボールを滑らかな斜面上で転がします。高さ0の場所までボールが転がるとき、ボールの速さを求めましょう。なお、重力加速度は\(g\)です。
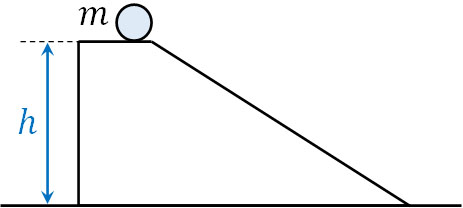
ボールがもつ位置エネルギーは\(mgh\)です。位置エネルギーがすべて運動エネルギーに変わるため、力学的エネルギー保存則より、以下の式を作ることができます。
\(mgh=\displaystyle\frac{1}{2}mv^2\)
\(v^2=2gh\)
\(v=\sqrt{2gh}\) (\(v>0\))
こうして、高さ0でのボールの速さは\(\sqrt{2gh}\)とわかります。
仕事とエネルギーの関係を理解する
力学を学ぶとき、仕事とエネルギーの関係を理解するのは重要です。そのためには、仕事の定義を覚えなければいけません。加えた力と移動距離をかけることにより、仕事の大きさを計算できます。
また物体にエネルギーを与えると、物体は運動エネルギーや位置エネルギー、弾性エネルギーをもつようになります。エネルギーの変化量が仕事であり、ジュール(J)を用いて仕事の大きさを表すことができます。
摩擦力や抵抗力が働いていない場合、運動エネルギーや位置エネルギー、弾性エネルギーを足すと常に一定になります。これを力学的エネルギー保存則と呼び、物理の計算問題ではひんぱんに利用されます。
運動エネルギーや位置エネルギーの計算をするとき、仕事を利用しましょう。物体の運動と同じ向きに加わる力を確認することで、仕事とエネルギーの計算を行えるようになります。






