熱を加えると気体分子は活発に動くようになります。言い換えると、熱によって分子のスピードが速くなります。
また熱を加えることによって分子の動きが活発化すると、体積が増えます。気体の体積が増えることにより、気体は仕事をします。このとき加えた熱量に対して、内部エネルギーと仕事の変化が一致する法則を熱力学第一法則といいます。
熱力学第一法則を利用できるようにするためには、気体の内部エネルギーと仕事の関係を学ばなければいけません。また気体が外部とやり取りをしない場合、内部エネルギーが保存されます。内部エネルギーの保存は熱力学第一法則を学ぶことによって理解できます。
それでは、どのように熱力学第一法則を用いればいいのでしょうか。また、内部エネルギーと仕事をどのように計算すればいいのでしょうか。熱力学第一法則の詳細を確認していきます。
もくじ
熱力学第一法則とは何か
まず、熱力学第一法則とは何かを理解しましょう。熱力学第一法則とは、「加えた熱量\(Q\)は内部エネルギーの変化量\(ΔU\)と気体が行った仕事量\(W\)の和に等しい」という法則です。
- \(Q=ΔU+W\)
熱力学第一法則は難しくありません。私たちが日常的に経験していることを数式で表しているだけです。
内部エネルギーとは、分子の運動エネルギーの総和を指します。分子の運動は温度に依存します。つまり分子のスピードが速いというのは、言い換えると温度\(T\)が高いことを意味しています。熱を加えると、当然ながら内部エネルギー(温度)は上昇します。
また熱を加えると、気体は膨張します。つまり、体積が増えます。体積が増えると、その分だけ気体は物体を押します。気体が特定の力で物体を押すことになるため、気体は仕事をします。
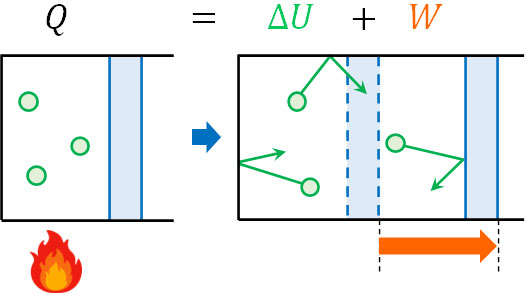
熱を加えることによって内部エネルギー(温度)が上昇したり、気体の体積増加によって気体が仕事をしたりするのは誰でも理解できます。そこで内部エネルギー変化と気体による仕事量を利用することにより、熱量を計算できるというわけです。
気体の内部エネルギーの公式
それでは、内部エネルギーはどのように計算すればいいのでしょうか。気体による仕事\(W\)は概念が簡単であり、圧力\(P\)と体積の変化量\(ΔV\)をかけることによって得られます。
- \(W=PΔV\) (圧力は一定)
一方で内部エネルギーを学ぶためには、気体の分子運動と圧力の関係を理解している必要があります。そのため、「あなたが気体の分子運動を理解している」という前提で解説していきます。
理想気体について、分子の運動エネルギーの総和を内部エネルギーといいます。気体の分子運動を計算すると、最終的に分子の運動エネルギーと温度の関係を計算できます。気体の分子運動より、一つの分子の運動エネルギーは以下のように計算できます。
- \(\displaystyle\frac{1}{2}m\overline{v^2}=\displaystyle\frac{3R}{2N_A}T\)
そこでこの式に対して、容器に存在する分子数をかけましょう。そうすれば、容器内に存在する分子の運動エネルギーの総和(内部エネルギー)を計算できます。
容器内に\(n\)molの分子が存在する場合、アボガドロ数\(N_A\)をかけることによって、容器に存在するすべての分子数を得ることができます。そのため容器内に存在する分子の運動エネルギーの総和(内部エネルギー\(U\))は以下になります。
\(U=\displaystyle\frac{3R}{2N_A}T×nN_A\)
\(U=\displaystyle\frac{3}{2}nRT\)
こうして、内部エネルギーの公式\(U=\displaystyle\frac{3}{2}nRT\)を得ることができました。理想気体の状態方程式である\(PV=nRT\)と内部エネルギーの公式は似ています。熱力学では内部エネルギーの計算をひんぱんに行うため、この公式を覚える必要があります。
なお、\(R\)は定数なので値は変化しません。つまり、内部エネルギーは物質量\(n\)と温度\(T\)に依存します。
ちなみに、内部エネルギーの公式が成り立つのは理想気体であるだけでなく、単原子分子である必要があります。具体的には、希ガス(ヘリウム、ネオン、アルゴンなど)であれば先ほど計算した内部エネルギーの公式が成立すると理解しましょう。高校物理での熱力学では、「単原子分子による理想気体を取り扱う」という前提があります。
密閉容器の場合、物質量\(n\)は一定となる
それでは、内部エネルギーの公式をより詳しく確認しましょう。熱力学第一法則では、内部エネルギーの変化量を利用します。そこで、内部エネルギーの変化量\(ΔU\)が何を意味しているのか学ぶのです。
密閉容器に熱を加えることで内部エネルギー(温度)の上昇や気体による仕事が行われる場面を考えましょう。この場合、物質量\(n\)は変化しません。
内部エネルギーは物質量と温度に依存するため、物質量が一定の場合、内部エネルギーの増減に関与するのは温度のみです。そのため密閉容器での内部エネルギー変化というのは、言い換えると温度の変化と捉えることができます。
それでは内部エネルギーの公式を利用することで、内部エネルギーの変化量を得る式を作りましょう。温度が\(T\)のとき、温度が\(ΔT\)だけ変化する場面を考えるのです。例えば「温度が300Kから320Kへと変化する場面での内部エネルギーを計算する」などです。
変化の度合いを計算したい場合、後の状態から前の状態を引けばいいです。そのため熱を加える前の温度を\(T\)、熱を加えた後の温度を\(T+ΔT\)としましょう。この場合、以下のように内部エネルギーの変化量\(ΔU\)を計算できます。
\(ΔU=\displaystyle\frac{3}{2}nR(T+ΔT)\)\(-\displaystyle\frac{3}{2}nRT\)
\(=\displaystyle\frac{3}{2}nRΔT\)
物質量が同じ場合、内部エネルギーの変化量\(ΔU\)は温度変化\(ΔT\)に依存するとわかります。熱力学第一法則では、温度変化に着目して内部エネルギーの変化量\(ΔU\)を計算しましょう。
内部エネルギーと仕事により、熱量を計算する
それでは、ここまで解説した内容を参考にして内部エネルギーと仕事による熱量を計算してみましょう。例えば、以下の問題の答えは何でしょうか。
- ピストンを内部へ押し、100Jの仕事をしました。内部エネルギーが40J上昇した場合、外部とやり取りした熱量はいくらでしょうか。
ピストンを内部へ押すため、気体の体積は減っています。気体は仕事をされているため、\(W=-100\)Jです。一方、内部エネルギーは40J増えているので以下の式を作ることができます。
\(Q=40-100\)
\(Q=-60\)
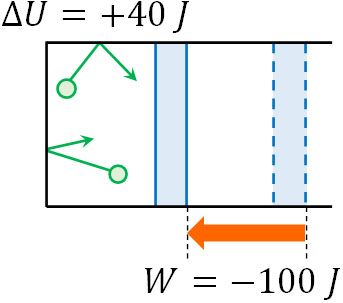
外部とやり取りした熱量は-60Jです。つまり、60Jを失っていることになります。気体は仕事をされることによって内部エネルギー(温度)が上昇し、さらには外部へ熱を放出したというわけです。
次に、以下の問題を解きましょう。
- 温度を一定に保ち、シリンダーへ100Jの熱を加えました。気体が外部へした仕事\(W\)はいくらですか。
温度は一定に保たされているため、温度変化はありません。内部エネルギーの変化量は\(ΔU=\displaystyle\frac{3}{2}nRΔT\)によって計算するため、温度変化がない場合、内部エネルギーの変化はありません。\(ΔU=0\)であるため、以下の式を作ることができます。
\(100=0+W\)
こうして、気体が外部にした仕事\(W\)は100Jとわかります。
内部エネルギーの保存:断熱材を使用するときの熱量変化
次に、断熱材を利用するときの熱量変化を学びましょう。断熱材を利用する場合、外から熱が加えられることがなければ、熱が外へ逃げていくこともありません。つまり、熱量の変化はゼロです。
言い換えると、断熱材を使用する場合、内部エネルギーと仕事の和は常に一定になります。熱量の変化が0であるため、変化前と変化後を比較すると、内部エネルギーと仕事の和が変化しないのは当然です。それでは、以下の問題の答えは何でしょうか。
- 以下のように、2つの容器をつなぎ、全体を断熱材で覆います。容器1は圧力\(P\)、体積\(V\)、温度\(T\)であり、容器2は圧力\(3P\)、体積\(2V\)、温度\(4T\)です。コックを開け、平衡状態になるとき、容器全体での気体の圧力と絶対温度を求めましょう。

熱力学第一法則を利用して式を作りましょう。断熱材を利用しているため、熱の出入りはありません。つまり、熱量\(Q\)の変化はゼロです。
またコックを開けて平衡状態に達するとき、容器1と容器2の合計体積は変化していません。容器1と容器2の体積は変わっていないため、気体による仕事量は\(W=0\)です。
そのため熱力学第一法則を利用すると、\(ΔU=0\)であるとわかります。外部と熱のやり取りがなく、気体による仕事が行われない場合、内部エネルギーの総和は変化しません。これが内部エネルギーの保存です。
そこで内部エネルギーの保存を利用し、以下の式を作りましょう。なおコックを開け、平衡状態での絶対温度を\(T’\)とします。
\(\displaystyle\frac{3}{2}nRT+\displaystyle\frac{3}{2}nR·4T=\displaystyle\frac{3}{2}nRT’\)
\(14T=3T’\)
\(T’=\displaystyle\frac{3}{14}T\)
熱力学第一法則を利用することにより、平衡状態での絶対温度は\(T’=\displaystyle\frac{3}{14}T\)とわかりました。
また気体の状態方程式より、\(PV=nRT\)です。そのため、以下のように式を変形できます(コックを開け、平衡状態での圧力を\(P’\)とします)。
\(\displaystyle\frac{3}{2}nRT+\displaystyle\frac{3}{2}nR·4T=\displaystyle\frac{3}{2}nRT’\)
\(\displaystyle\frac{3}{2}PV+\displaystyle\frac{3}{2}·3P·2V=\displaystyle\frac{3}{2}·P’·3V\)
\(21P=9P’\)
\(P’=\displaystyle\frac{3}{7}P\)
気体の状態方程式と熱力学第一法則、内部エネルギーの保存を利用することにより、平衡状態での圧力は\(P’=\displaystyle\frac{3}{7}P\)と計算できました。
内部エネルギーの概念を学び、熱力学第一法則を利用する
熱力学で学ぶべき法則は複数あります。その中の一つが熱力学第一法則です。内容は難しくなく、熱を加えると温度(内部エネルギー)と気体による仕事が行われるのを表すのが熱力学第一法則です。
熱力学第一法則を利用できるようにするため、内部エネルギーの概念を学びましょう。内部エネルギーは物質量と温度によって決まります。また物質量が一定の場合、内部エネルギーの変化量は温度変化に依存します。
そこで内部エネルギーの公式と気体による仕事の公式を利用し、計算できるようになりましょう。特に断熱材を利用し、かつ気体による仕事が行われない場合、内部エネルギーの保存を利用しましょう。
熱力学を学ぶとき、基本的な内容の一つが熱力学第一法則です。内部エネルギーと気体による仕事を利用し、熱量を計算できるようになりましょう。






