交流電流でRLC直列回路とRLC並列回路を学んだのであれば、共振回路を理解できるようになります。インピーダンスを利用することにより、共振周波数を計算できるのです。最適な角周波数を選ぶことにより、流れる電流を最小にしたり、最大にしたりできます。
公式を覚えても意味がなく、共振周波数を計算できるようにならなければいけません。そこで、RLC直列回路とRLC並列回路でどのような現象が起こるのか学びましょう。
また共振回路では、コンデンサーとコイルで電荷のやり取りが行われています。これを電気振動といいます。電気振動が起こっている場合、電源からの電流は流れません。それでは、なぜこのような現象が起こるのでしょうか。
RLC回路でのインピーダンスの応用が共振回路と電気振動です。そこで、RLC回路で起こる現象をより深く確認しましょう。
もくじ
インピーダンス\(Z\)が最小または最大となる角周波数
既にRLC回路とインピーダンスを理解している前提で話を進めるため、これらの内容を理解していない場合、必ず事前にRLC回路について復習しましょう。
さて、RLC直列回路やRLC並列回路では、電圧やインピーダンスで以下のような関係があります。
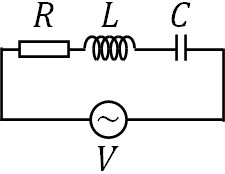
・RLC直列回路
- \(V_0=\sqrt{R^2+\left(ωL-\displaystyle\frac{1}{ωC}\right)^2}I_0\)
- \(Z=\sqrt{R^2+\left(ωL-\displaystyle\frac{1}{ωC}\right)^2}\)
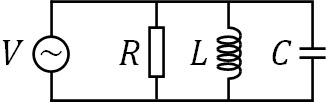
・RLC並列回路
- \(V_0=\displaystyle\frac{1}{\sqrt{\displaystyle\frac{1}{R^2}+\left(ωC-\displaystyle\frac{1}{ωL}\right)^2}}I_0\)
- \(Z=\displaystyle\frac{1}{\sqrt{\displaystyle\frac{1}{R^2}+\left(ωC-\displaystyle\frac{1}{ωL}\right)^2}}\)
RLC直列回路とRLC並列回路のインピーダンス\(Z\)の式を確認すると、抵抗\(R\)や自己インダクタンス\(L\)、電気容量\(C\)の値は一定です。変化するのは角周波数\(ω\)のみです。つまり、回路全体の抵抗(インピーダンス)は角周波数\(ω\)に依存するとわかります。
また、RLC直列回路のインピーダンスを逆数にすると、RLC並列回路のインピーダンスになります。つまり、RLC直列回路のインピーダンスとRLC並列回路のインピーダンスは式が似ているのです。
RLC直列回路でインピーダンス\(Z\)が最小になるためには、\(ωC-\displaystyle\frac{1}{ωL}\)がゼロであればいいです。またRLC並列回路でインピーダンス\(Z\)が最大になるためには、分母の値が小さくなればいいため、\(ωC-\displaystyle\frac{1}{ωL}\)がゼロであればいいです。
つまりRLC回路では、\(ωC-\displaystyle\frac{1}{ωL}\)がゼロの場合、インピーダンスで最小値または最大値を得ることができます。言い換えると角周波数\(ω\)には、コンデンサーとコイルによる影響が同じとなる最適な値が存在するのです。
そこで、以下のように計算しましょう。
\(ωC-\displaystyle\frac{1}{ωL}=0\)
\(ω^2=\displaystyle\frac{1}{CL}\)
\(ω=\displaystyle\frac{1}{\sqrt{CL}}\)
計算することにより、\(ω=\displaystyle\frac{1}{\sqrt{CL}}\)のときにインピーダンス\(Z\)が最小または最大になるとわかります
共振周波数\(f\)の計算:直列共振と並列共振
それでは、\(ω=\displaystyle\frac{1}{\sqrt{CL}}\)であるとき、周波数\(f\)を計算しましょう。1秒で進むスピードが角周波数\(ω\)であるため、周期\(T\)をかけると、必ず\(2π\)(360°)となります。そのため、\(ωT=2π\)です。
また周期\(T\)と周波数\(f\)には、\(T=\displaystyle\frac{1}{f}\)の関係があります。そこで、以下のように計算しましょう。
\(ωT=2π\)
\(\displaystyle\frac{1}{\sqrt{CL}}×\displaystyle\frac{1}{f}=2π\)
\(f=\displaystyle\frac{1}{2π\sqrt{CL}}\)
こうして、インピーダンスが最小または最大となるときの周波数\(f\)を得ることができました。また、\(f=\displaystyle\frac{1}{2π\sqrt{CL}}\)となる振動数を共振周波数といいます。共振周波数を公式をとして覚えても意味がないため、必ず式を導出できるようになりましょう。
・RLC直列回路での直列共振
RLC直列回路でのインピーダンスを再び記すと以下のようになります。
- \(Z=\sqrt{R^2+\left(ωL-\displaystyle\frac{1}{ωC}\right)^2}\)
式を確認してわかる通り、\(ωC=\displaystyle\frac{1}{ωL}\)となっている共振回路では、インピーダンス\(Z\)は最小値となります。つまり、直列共振が起こっているときは回路全体の抵抗が最小値である\(R\)となり、電流の大きさは最大となります。
・RLC並列回路での並列共振
次に、RLC並列回路でのインピーダンスを確認しましょう。以下のようになります。
- \(Z=\displaystyle\frac{1}{\sqrt{\displaystyle\frac{1}{R^2}+\left(ωC-\displaystyle\frac{1}{ωL}\right)^2}}\)
\(ωC=\displaystyle\frac{1}{ωL}\)となる共振回路では、分母が最小値となるため、インピーダンス\(Z\)は最大値となります。つまり並列共振が起こっている場合、回路全体の抵抗は最大値である\(R\)となります。抵抗は最大となるため、電流は最小値となります。
共振周波数によって共振が起こるとき、直列共振でも並列共振でもインピーダンスの値は\(R\)であり同じです。ただ直列共振ではインピーダンスが最小値であり、並列共振ではインピーダンスが最大値となるため、意味が大きく異なります。
アンテナの原理と共振周波数の関係
波では、共振を共鳴といいます。特定の振動数(固有振動数)によって波を起こすとき、物体が大きく振動する現象が共振です。
例えば直列共振が起こっているとき、前述の通り抵抗が最小値となり、電流の値が最大値となります。つまり、特定の周波数のときのみ、交流回路で大きな電流を流すように設定できるのです。
共振周波数を利用している例にアンテナなどの受信回路があります。
例えばテレビアンテナであれば、テレビ番組ごとにあらかじめ周波数を決めておき、特定の周波数のみ受信する装置を作っておきます。テレビ番組を変えるとき、特定の周波数(共振周波数)では大きな電流を流し、それ以外の周波数では電流が流れないように調節するのです。
アンテナなど、電波の送受信をするとき、共振回路が重要になります。共振周波数を利用することにより、目的の周波数のみ選択できるのです。これが、共振回路を利用するアンテナの原理です。
並列共振回路とコンデンサー・コイルの関係
それでは、共振周波数による並列共振回路について、より深く確認しましょう。並列共振回路では、どのような現象が起こっているのでしょうか。
\(ωC=\displaystyle\frac{1}{ωL}\)となる場合、RLC並列回路のインピーダンスの式を見てわかる通り、回路全体の抵抗は\(R\)になります。つまり、すべての電流は抵抗に流れていることを意味します。
この場合、電源とコイル・コンデンサーは切り離されていると考えることができます。そのため並列共振回路では、以下のように回路を変えることができます。
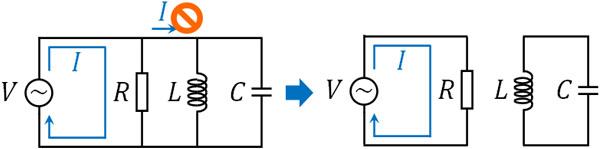
導線でつながってはいるものの、電流が流れていないため、実質的に断線していると考えることができるのです。
電荷が往復する現象が電気振動
それでは、コイルとコンデンサーにはまったく電流が流れていないのでしょうか。実は、コイルとコンデンサーには電流が流れています。電源から断線しているにも関わらず、コイルとコンデンサーに電流が流れるというのは、どういう意味なのでしょうか。
電荷を有するコンデンサーに対してコイルを接続すると、電荷はコンデンサーとコイルを行ったり来たりします。つまり、あるときはコンデンサーからコイルに電流が流れ、そのあとにコイルからコンデンサーへ電流が流れます。これを繰り返すのです。この現象を電気振動といいます。
電気振動が起こる理由については、RLC並列回路でのベクトル図を利用すれば理解できます。RLC並列回路について、わかりやすくするため、\(sinωt=0\)のときの図を確認しましょう。なお、コイル(L)の電流を\(I_L\)、コンデンサー(C)の電流を\(I_C\)とします。
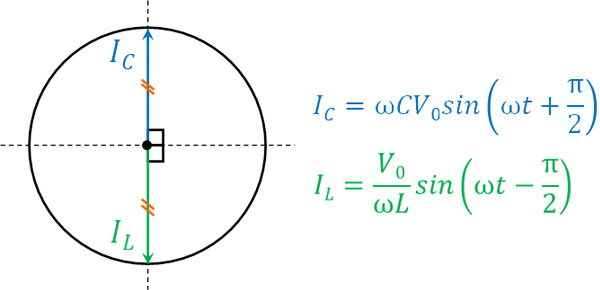
円運動での角度(\(ωt\))は変化します。ただ、上図のように\(I_L\)と\(I_C\)の向きは常に180°であり、さらには共振回路なので線の長さが同じです。\(ωC=\displaystyle\frac{1}{ωL}\)であるため、\(I_L=-I_C\)となるのです。そのため、ベクトルを足すと常にゼロになります。
ただベクトルは打ち消し合うことによってゼロになっているものの、それぞれの要素がゼロというわけではありません。同じ大きさにて、反対向きに電流が流れているのです。
電気振動では\(\displaystyle\frac{T}{4}\)ごとに電荷や電流が変化する
それでは、電気振動では具体的にどのような変化が起こっているのでしょうか。荷電しているコンデンサーとコイルについて、スイッチを入れることで接続する場面を考えましょう。
電荷を蓄積しているコンデンサーは電源と捉えることができます。そのためスイッチを入れると、コイルへ電流が流れます。ただコイルは磁場の変化を嫌う性質があるため、コンデンサーとコイルをつないでも電流は流れません。
ただ時間が経過すると、コンデンサーに溜まっていた電荷は徐々にコイルへ流れていきます。つまり、電流が流れます。そうして、最終的にコンデンサーの電荷はゼロになり、このとき電流の値は最大になります。
しかし、コンデンサーの電荷がゼロになっても放電は終わりません。コイルは磁場の変化を嫌うため、電流が弱まることによって磁場が弱くなるのを防ぐため、コイルは電磁誘導によって電流を作り続けます。その結果、コンデンサーは最初とは逆向きで電荷を帯びます。
そうして、今度は逆向きに電流が流れ、これが繰り返されます。具体的には、周期\(T\)に対して、\(\displaystyle\frac{T}{4}\)の時間が経過するごとに以下の変化を繰り返すのです。
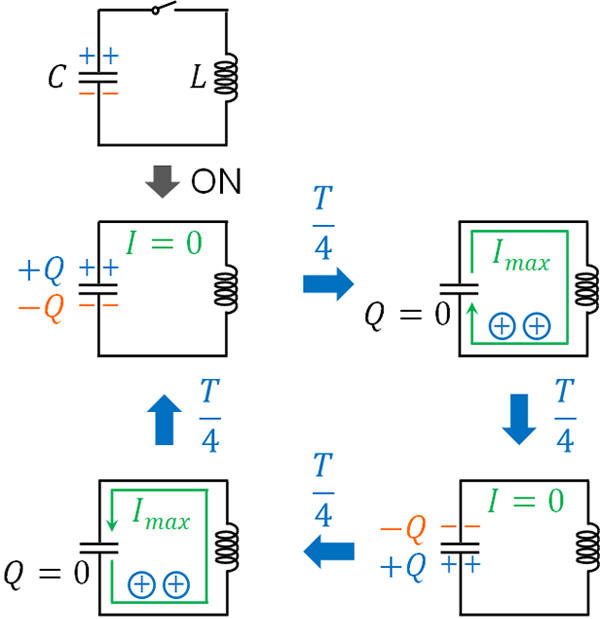
これが、電気振動で起こっている現象の詳細です。
LC並列部でのエネルギー保存則
なお並列共振回路では、電源からの電流がコイル(L)とコンデンサー(C)に流れていないため、電源は仕事をしていません。そのため、エネルギー保存則が成り立ちます。
またコイルとコンデンサーはエネルギーを蓄積することが知られています。エネルギーを得るそれぞれの公式は以下になります。
- コイル:\(\displaystyle\frac{1}{2}LI^2\)
- コンデンサー:\(\displaystyle\frac{1}{2}CV^2\)
そのためエネルギー保存則を利用すると、以下の関係が成り立ちます。
- \(\displaystyle\frac{1}{2}LI^2+\displaystyle\frac{1}{2}CV^2=\)一定
例えば振動電流の最大値を求めたい場合、\(\displaystyle\frac{1}{2}CV^2=0\)のときの\(\displaystyle\frac{1}{2}LI^2\)を計算すればいいとわかります。振動電流が最大値\(I_{max}\)になるとき、コンデンサーの電荷はゼロだからです。
エネルギー保存則を利用することにより、コンデンサーに蓄積している電気量や回路を流れる電流の大きさを計算できるようになります。
共振回路で起こっている現象を学ぶ
RLC回路では、共振周波数を利用することによって抵抗が最小または最大になります。RLC直列回路では共振周波数によって抵抗が最小となり、RLC並列回路では共振周波数によって抵抗が最大となるのです。
共振周波数というのは、最適な周波数ともいえます。共振周波数を利用することによって共振回路となり、特定の電波を選択できるようになります。
また並列共振回路では電気振動という現象が起こります。並列共振回路では、コンデンサーとコイルに対して電源由来の電流は流れません。ただ、コンデンサーとコイルでは電荷が行ったり来たりしています。つまり、電流が相互に流れています。
RLC回路を学んでいないと、共振回路と電気振動を理解することはできません。また、公式を導出できるようになりましょう。そうすれば、共振回路や電気振動でどのような現象が起こっているのかわかります。






