電流と抵抗：オームの法則と電圧・電流・抵抗の関係

電気を学ぶとき、重要な内容に電流があります。自由電子が動くことによって電流が発生します。私たちは電気を毎日の生活で利用しており、電流が発生することで電気を使えるのです。電気量と時間を利用することにより、電流の計算が可能です。また、電流の定義も理解できます。

電流にはルールがあります。自由電子が動く向きと電流の向きは逆であるため、この事実を知っておかなければいけません。

また電流が流れるとき、抵抗が発生します。電圧と電流を利用することによって抵抗の計算が可能です。このとき利用する法則がオームの法則です。また、抵抗は断面積と長さを利用することでも計算できます。

それでは、どのように電流と抵抗を計算すればいいのでしょうか。定義や公式の意味を含めて、電流と抵抗を解説していきます。

正電荷から負電荷への流れが電流：自由電子の向きは逆

電池を利用し、導線をつなぐことによって電球に明かりをつけることができます。電池によって電流が発生するからです。正電荷から負電荷へ電流が流れるのです。図にすると、電流の向きは以下のようになります。

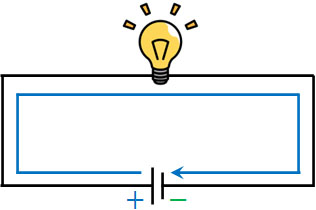
なぜ、電流が正電荷から負電荷に流れるかというと、大昔の学者がそのように決めたからです。

電流が本当に正電荷から負電荷に流れているかどうか、当時の学者にとって不明です。ただ、定義しないと法則を作ることができません。そこで、彼らは電流の向きを決めたのです。

・電流の向きと電子が流れる向きは逆

それでは、電流の正体は何でしょうか。既に知っている通り、自由電子が動くことによって電流が発生します。電流の正体は自由電子なのです。そのため本来であれば、自由電子と電流の向きは同じでなければいけません。

1890年ごろ、物理学者トムソンによって電子が発見され、電子が動くことによって電流が発生することがわかりました。また、電子は負極から正極へ動くことを報告しました。

ただ電流の向きは正電荷から負電荷になると定義されており、右ねじの法則やフレミングの左手の法則など、多くの法則が既に報告されています。そのため電流の向きを変えると、それまで多くの人が利用していた法則について、符号が逆になって不都合です。

そこで大昔の人が決めた電流の向きをいまでも私たちは利用しています。電流の向きが自由電子の向きと異なることに大きな意味はなく、「そのように決められているから」と考えて納得しましょう。

一秒間に流れる電気量\(Q\)が電流の定義

それでは、電流はどのように定義されているのでしょうか。物質が電荷をもつとき、重要な単位に電気量\(Q\)があります。このとき、どれだけの電気量\(Q\)が流れたのかを表すのが電流です。より正確にいうと、一秒に流れる電気量\(Q\)が電流の定義です。

例えば\(t\)秒間に電気量\(Q\)が流れる場合、電流\(I\)は以下の式によって得られます。

• \(I=\displaystyle\frac{Q}{t}\)

電流の定義を理解している場合、この公式を覚えなくても式を作ることができます。

電流というのは、川の流れと似ています。水の流れが激しいというのは、1秒間に流れる水の量が多いことを意味しています。同じように、電流が大きいというのは、流れる自由電子の数が多いことを意味しています。

自由電子の数が多いと、当然ながらその分だけ電気量\(Q\)が大きくなります。そこで自由電子による電気の合計（電気量\(Q\)）を利用し、時間\(t\)で割ることによって電流を得るのです。なお電流の単位はA（アンペア）です。

・電流と時間から電気量の計算が可能

\(I=\displaystyle\frac{Q}{t}\)によって電流を得ることができるため、この公式を以下のように変形しましょう。

• \(Q=It\)

電流\(I\)と時間\(t\)をかけることによって、電気量\(Q\)を得ることができます。電流の定義を学ぶとき、電流と電気量、時間の関係を理解しましょう。

電子の数、速さ、導線の断面積から電流を得る

なお電子が動くことによって電流が発生しているため、どれだけの数の電子が動いているのかによって電流の大きさを計算できます。

例えば川を流れる水というのは、川を流れる水の断面積\(S\)が大きいほど、水のスピード\(v\)が速いほど水量が多くなります。同様に導線の断面積\(S\)が大きいほど、電子が動くスピード\(v\)が速いほど、電気量は大きくなります。

速さは\(v\)[m/s]であるため、\(t\)秒が経過する場合、動いた距離は\(vt\)[m]です。また断面積が\(S\)[m²]の場合、電子が\(t\)秒で動く体積は\(vtS\)[m³]です。

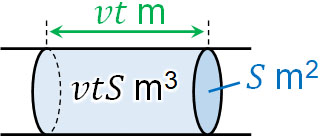
このとき、1m³に\(n\)個の電子がある場合を考えてみましょう。この場合、\(vtS\)[m³]に存在する電子の総数は\(nvtS\)[個]です。また1個の電子の電気量を\(-e\)[C]とすると、合計の電気量\(Q\)は以下のようになります。

• \(Q=envtS\)

こうして、1個の電子がもつ電気量を利用することによって、全体の電気量を計算できます。なお前述の通り、一秒に流れる電気量\(Q\)が電流\(I\)です。そのため、電流\(I\)を得る式は以下になります。

• \(I=envS\)

\(I=\displaystyle\frac{Q}{t}\)であるため、先ほどの式から\(t\)を取り去りましょう。そうすれば、電流\(I\)を計算できます。

抵抗とオームの法則：電圧、電流、抵抗の関係

電流を学んだら、抵抗を理解できます。電熱線に電流を流すと、電熱線は熱くなります。これは、電熱線が強い抵抗をもつからです。抵抗によって電気は熱エネルギーへと変換されるのです。

電荷に対して摩擦を生じると熱くなります。抵抗というのは、電荷の動きを妨げる物体と理解しましょう。

多くの場合、抵抗\(R\)に対して電圧\(V\)と電流\(I\)は比例関係になっていることがわかっています。つまり、以下の公式が成り立ちます。

• \(V=RI\)

これをオームの法則といいます。抵抗\(R\)の単位はΩ（オーム）であり、抵抗が大きくなるほど電荷の動きは鈍くなります。

電気抵抗がある場合、その分だけ電圧が消費されます。つまり抵抗につながっている導線では、両端で電位差を生じています。この電位差を電圧降下といいます。抵抗を通ると、必ず電位が低下するのです。

なおオームの法則での電圧\(V\)というのは、抵抗にかかる電圧を表しています。言い換えると、抵抗による電圧降下が\(V\)です。電源の電圧は関係ないので注意しましょう。

抵抗の断面積\(S\)と長さ\(l\)から抵抗\(R\)を得る

オームの法則は非常に有名であり、抵抗\(R\)を利用することで、電圧\(V\)と電流\(I\)が比例関係になる事実を覚えましょう。それでは、抵抗\(R\)はどのように値が決定されるのでしょうか。

電気の流れにくさを表すのが抵抗であるため、抵抗は荒い道と捉えることができます。あなたが荒い道を進むとき、荒い道の距離\(l\)が長いほど進みにくいです。

また、道幅が狭い場合は通りにくく、道幅が広い場合は通りやすいです。導線では、断面積\(S\)が道幅に該当します。

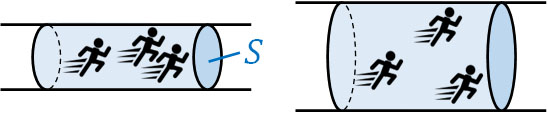
そこで、比例定数\(ρ\)（ロー）を用いて抵抗\(R\)を表すと以下の公式を得られます。

• \(R=ρ\displaystyle\frac{l}{S}\)

比例定数\(ρ\)は抵抗率[Ω·m]と呼ばれており、物質の違いによって\(ρ\)の値は変化します。また先ほどの公式を確認すると、距離\(l\)が長いほど抵抗が大きくなり、断面積\(S\)が大きいほど抵抗が小さくなります。

このように確認すると、なぜ\(R=ρ\displaystyle\frac{l}{S}\)によって抵抗を計算できるのか理解できます。距離が長いほど、断面積が小さいほど、抵抗が大きくなるのは当然であり、これを式で表すのです。

抵抗の温度変化と温度係数

参考までに、抵抗は温度変化による影響を受けます。一般的には、金属などの導体は温度が低いと抵抗が小さくなり、温度が高いと抵抗が大きくなります。一方で不導体や半導体では、温度が高いほど抵抗が小さくなりやすいです。

このとき、0℃での抵抗率を\(ρ_0\)とすると、\(T\)[℃]での抵抗率\(ρ\)を以下の式で表すことができます。

• \(ρ=ρ_0(1+αT)\)

αは抵抗率の温度係数と呼ばれており、物質によって異なります。また金属では温度が高いと抵抗率が大きくなるため、αは正の値です。一方で不導体や半導体では温度が高いほど抵抗が低くなるため、αは負の値です。

電流と抵抗に関する練習問題

それでは、電流と抵抗に関する練習問題を解いてみましょう。以下の問題の答えは何でしょうか。

• 下図のように長さ\(l\)[m]、断面積\(S\)[m²]の金属棒の両端に電圧\(V\)を加えました。電子一つの電気量を\(-e\)、1m³に存在する電子数を\(n\)、電子が金属棒の中を移動するスピードを\(v\)[m/s]とします。

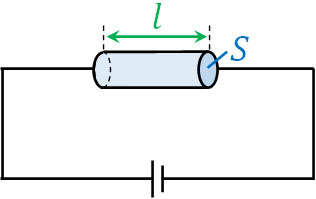
1. 金属内の電場の大きさ\(E\)と向き、電子が電場から受ける力\(F\)の大きさを求めましょう。
2. 電子が受ける抵抗力が比例定数\(k\)での速さ\(v\)に比例するとき、一定の速さ\(v\)の値を求めましょう。
3. 速さ\(v\)を利用せず、電流\(I\)を式で表しましょう。
4. 金属棒の抵抗率はいくらですか。

1) 金属内の電場の大きさと向き、電子が電場から受ける力の大きさを求めましょう

公式より、\(V=Ed\)であるため、\(E=\displaystyle\frac{V}{d}\)です。そこでこの公式に代入すると、電場\(E\)は\(E=\displaystyle\frac{V}{l}\)とわかります。なお電場の向きは正電荷から負電荷であるため、電場は右向きです。

また\(F=qE\)であるため、一つの電子が電場から受ける力は\(F=\displaystyle\frac{eV}{l}\)です。

2) 電子が受ける抵抗力が比例定数\(k\)での速さ\(v\)に比例するとき、一定の速さ\(v\)の値を求めましょう

電子は一定の速さ\(v\)で進むため、加速度がありません。つまり、抵抗力\(kv\)と電場から受ける力\(F=\displaystyle\frac{eV}{l}\)がつり合っています。そこで、以下の式を作りましょう。

\(kv=\displaystyle\frac{eV}{l}\)

\(v=\displaystyle\frac{eV}{kl}\)

こうして、\(v=\displaystyle\frac{eV}{kl}\)と計算できました。

3) 速さ\(v\)を利用せず、電流\(I\)を式で表しましょう

\(t\)秒で電子が金属棒を通過する場合、金属棒の長さは\(vt\)[m]です。そのため金属の体積は\(vtS\)[m³]です。電子一つの電気量\(e\)と1m³に存在する電子数\(n\)をかけると、全体の電気量\(Q\)を得られます。

• \(Q=envtS\)

また\(Q=It\)であるため、電流\(I\)は以下の式によって得られます。

• \(I=envS\)

ここまでは既に解説した通りです。そこで、\(v=\displaystyle\frac{eV}{kl}\)を\(I=envS\)に代入しましょう。

\(I=envS\)

\(I=enS×\displaystyle\frac{eV}{kl}\)

\(I=\displaystyle\frac{e^2nSV}{kl}\)

こうして、 速さ\(v\)を利用せず、電流\(I\)を表すことができました。

4) 金属棒の抵抗率はいくらですか

抵抗率を計算する必要があるため、先に抵抗\(R\)を計算しましょう。オームの法則より、\(V=RI\)であるため、\(R=\displaystyle\frac{V}{I}\)です。そこで、\(I=\displaystyle\frac{e^2nSV}{kl}\)を代入しましょう。

\(R=\displaystyle\frac{V}{I}\)

\(R=V×\displaystyle\frac{kl}{e^2nSV}\)

\(R=\displaystyle\frac{kl}{e^2nS}\)

なお抵抗率を\(ρ\)とすると、抵抗\(R\)は長さ\(l\)に比例し、断面積\(S\)に反比例することがわかっています。そのため既に解説した通り、\(R=ρ\displaystyle\frac{l}{S}\)となります。そこで、この公式を利用して抵抗率を求めましょう。

\(R=ρ\displaystyle\frac{l}{S}\)

\(ρ=R\displaystyle\frac{S}{l}\)

\(ρ=\displaystyle\frac{kl}{e^2nS}×\displaystyle\frac{S}{l}\)

\(ρ=\displaystyle\frac{k}{e^2n}\)

こうして、抵抗率は\(ρ=\displaystyle\frac{k}{e^2n}\)になるとわかります。

電流と抵抗の関係を学び、オームの法則を利用する

電気が流れている場合、必ず電流が存在します。電流は正電荷から負電荷へ流れ、電気量\(Q\)と時間\(t\)を利用して、\(I=\displaystyle\frac{Q}{t}\)と表すことができます。または、一つの電子がもつ電気量を利用して、\(I=envS\)と表すこともできます。

なお電流を学ぶとき、同時に抵抗も理解しましょう。オームの法則によって\(V=RI\)と表すことができ、電圧・電流・抵抗の関係を学ぶことになります。

このときオームの法則に加えて、抵抗率\(ρ\)を用いて抵抗\(R\)を計算できるようになりましょう。荒い道を想像すれば、なぜ抵抗\(R\)が長さ\(l\)に比例し、断面積\(S\)に反比例するのか理解できます。

電気では複数の公式を利用して計算することになります。ただ公式を暗記しても忘れやすいですし、応用問題が出されると計算問題を解けません。そこで公式を作れるようになり、公式が何を意味しているのかを学ぶことで計算できるようになりましょう。